Tính V hình chóp \(\Delta\) đều SABC biết cạnh đáy = a , \(\widehat{SBC}=60^o\) .
Help me !!!
Những câu hỏi liên quan
Cho hình chóp SABC có đáy là tam giác đều cạnh a, SA vuông góc với mặt phẳng đáy, góc giữa hai mặt phẳng (SBC) và (ABC) bằng
60
°
. Tính thể tích V của khối chóp SABC A.
V
a
3
3
8
B.
V
a
3
12
C.
V...
Đọc tiếp
Cho hình chóp SABC có đáy là tam giác đều cạnh a, SA vuông góc với mặt phẳng đáy, góc giữa hai mặt phẳng (SBC) và (ABC) bằng 60 ° . Tính thể tích V của khối chóp SABC
A. V = a 3 3 8
B. V = a 3 12
C. V = a 3 3 4
D. V = a 3 3 12
4 tháng 5 2021 lúc 21:18
Cho hình chóp đều SABC cạnh đáy bằng a. Tâm O góc giữa (SBC) và đáy bằng 60°. Tính khoảng cách từ a)O đến (SAB) b)C đến (SAB)
Cho hình chóp SABC có đáy ABC là tam giác vuông cân tại A, độ dài ABACa. Biết rằng Delta SAB có góc widehat{ABS}60^0 và nằm trong mặt phẳng vuông góc với mặt đáy. Tính khoảng cách từ điểm A đến mp(SBC) theo a .P/s: em nhờ quý thầy cô giáo và các bạn yêu toán giúp đỡ em với ạ, em cám ơn nhiều ạ!
Đọc tiếp
Cho hình chóp SABC có đáy ABC là tam giác vuông cân tại A, độ dài \(AB=AC=a\).
Biết rằng \(\Delta SAB\) có góc \(\widehat{ABS}=60^0\) và nằm trong mặt phẳng vuông góc với mặt đáy.
Tính khoảng cách từ điểm A đến mp(SBC) theo \(a\) .
P/s: em nhờ quý thầy cô giáo và các bạn yêu toán giúp đỡ em với ạ, em cám ơn nhiều ạ!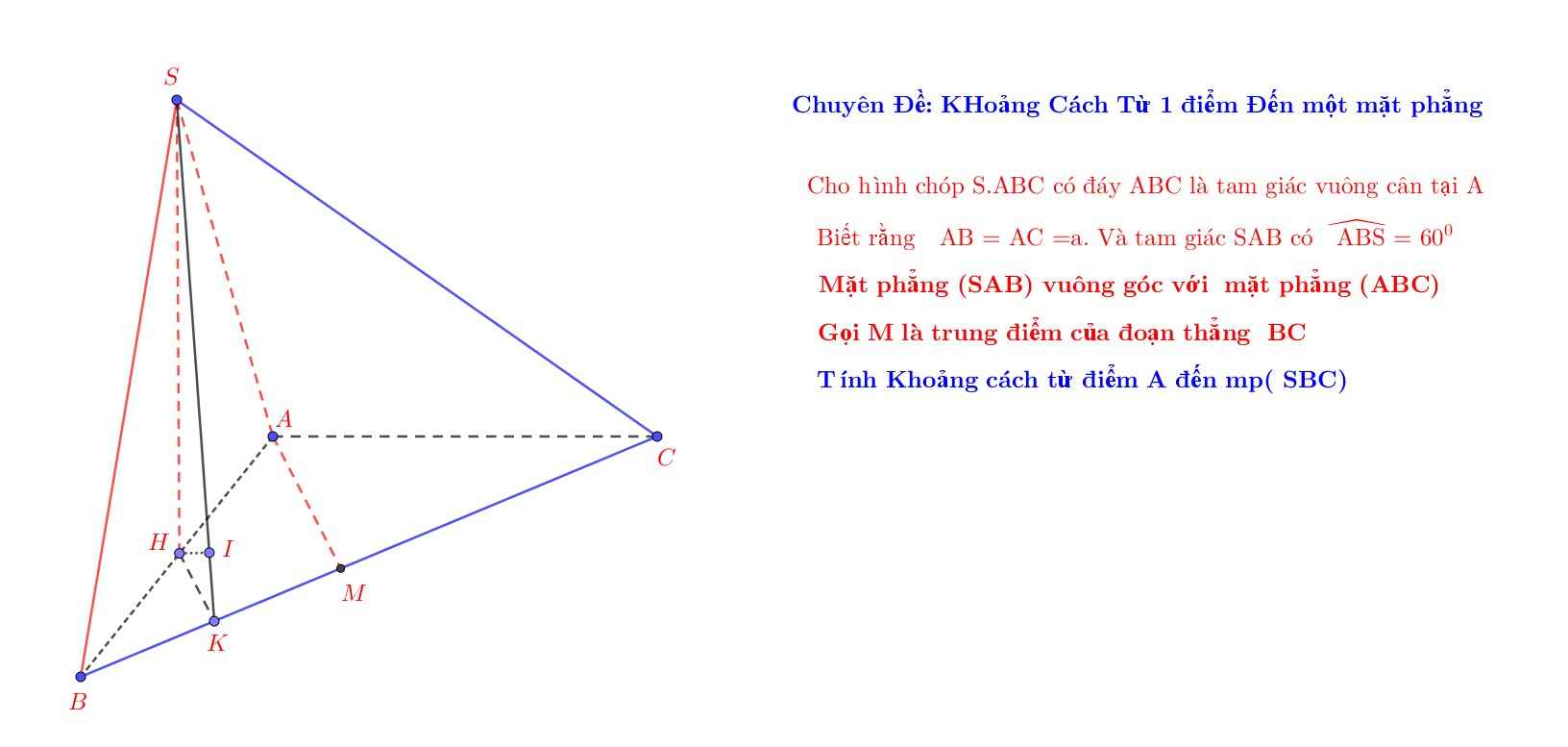
Hình bạn tự vẽ nha mình biếng á chứ khog có j đou=)
Ta có : \(\left\{{}\begin{matrix}CA\perp AB\\\left(ABC\right)\perp\left(SAB\right)\\\left(ABC\right)\cap\left(SAB\right)=AB\end{matrix}\right.\) \(\Rightarrow CA\perp\left(SAB\right)\)
Kẻ \(AK\perp SB\) và \(AH\perp CK\) tại H.
Ta có : \(\left\{{}\begin{matrix}SB\perp AK\\SB\perp CA\end{matrix}\right.\) \(\Rightarrow SB\perp\left(ACK\right)\Rightarrow SB\perp AH\)
Do : \(\left\{{}\begin{matrix}AH\perp CK\\AH\perp SB\end{matrix}\right.\) \(\Rightarrow AH\perp\left(SBC\right)\Rightarrow d\left(A;\left(SBC\right)\right)=AH\)
Xét t/g ABK , ta có : AK = AB
=> \(sin\widehat{ABK}=\alpha sin60^o=\dfrac{a\sqrt{3}}{2}\)
Xét t/g ACK , ta có : \(\dfrac{1}{AH^2}=\dfrac{1}{AK^2}+\dfrac{1}{AC^2}=\dfrac{7}{3a^2}\Rightarrow AH=\dfrac{a\sqrt{21}}{7}\)
Đúng 1
Bình luận (0)
Cho hình chóp SABC có đáy là tam giác đều cạnh a, SA vuông góc với mặt phẳng đáy, góc giữa hai mặt phẳng (SBC) và (ABC) bằng
60
0
. Tính thể tích V của khối chóp SABC.
Đọc tiếp
Cho hình chóp SABC có đáy là tam giác đều cạnh a, SA vuông góc với mặt phẳng đáy, góc giữa hai mặt phẳng (SBC) và (ABC) bằng 60 0 . Tính thể tích V của khối chóp SABC.
Cho hình chóp SABC có đáy là tam giác đều cạnh a, SA vuông góc với mặt phẳng đáy, góc giữa hai mặt phẳng (SBC) và (ABC) bằng
60
°
. Thể tích của khối chóp SABC bằng A.
a
3
3
8
B.
a
3
12
C.
a
3...
Đọc tiếp
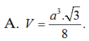
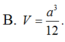
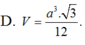
Cho hình chóp SABC có đáy là tam giác đều cạnh a, SA vuông góc với mặt phẳng đáy, góc giữa hai mặt phẳng (SBC) và (ABC) bằng 60 ° . Thể tích của khối chóp SABC bằng
A. a 3 3 8
B. a 3 12
C. a 3 3 4
D. a 3 3 12
24 tháng 8 2021 lúc 19:49
Cho hình chóp đều SABC cạnh đáy a. Cạnh bên tạo với đáy 1 góc 60°. Thể tích của mặt cầu ngoại tiếp hình chóp là V .Tính V/π/a³
Gọi O là tâm đáy \(\Rightarrow AO=\dfrac{a\sqrt{3}}{3}\)
\(SA=\dfrac{AO}{cos60^0}=\dfrac{2a\sqrt{3}}{3}\)
\(SO=\sqrt{SA^2-AO^2}=a\)
\(\Rightarrow R=\dfrac{SA^2}{2SO}=\dfrac{2a}{3}\)
\(V=\dfrac{4}{3}\pi R^3=\dfrac{32\pi a^3}{81}\)
\(\Rightarrow\dfrac{V}{\pi a^3}=\dfrac{32}{81}\)
Đúng 1
Bình luận (0)
a,Tính góc giữa SC và ( ABC) b, Tính góc giữa ( SBC ) Và ( ABC) Biết: 1,Hình chóp SABC có đáy ABC là tam giác đều cạnh bằng a, tam giác SAC cân tại S và nằm trong mặt phẳng vuông góc với đáy, SB hợp với đáy một góc 30 độ2, Hình chóp SABC có đáy ABC là tam giác đều , mặt bên SAB nằm trong mặt phẳng vuông góc với mặt phẳng đáy và tam giác SAB vuông tại S. SA asqrt{3}, SB a
Đọc tiếp
a,Tính góc giữa SC và ( ABC)
b, Tính góc giữa ( SBC ) Và ( ABC)
Biết:
1,Hình chóp SABC có đáy ABC là tam giác đều cạnh bằng a, tam giác SAC cân tại S và nằm trong mặt phẳng vuông góc với đáy, SB hợp với đáy một góc 30 độ
2, Hình chóp SABC có đáy ABC là tam giác đều , mặt bên SAB nằm trong mặt phẳng vuông góc với mặt phẳng đáy và tam giác SAB vuông tại S. SA= \(a\sqrt{3}\), SB= a
4 tháng 5 2021 lúc 20:31
Cho hình chóp đều SABC tâm O cạnh đáy bằng a cạnh bên SA = 3a tính khoảng cách từ E đến mặt phẳng SBC với E là trung điểm của SA
Cho hình chóp đều SABC, cạnh đáy bằng a, góc giữa cạnh bên và mặt đáy bằng
60
°
. Tính thể tích của khối chóp SABC A.
a
3
3
12
B.
a
3
12
C.
a
3
3
4...
Đọc tiếp
Cho hình chóp đều SABC, cạnh đáy bằng a, góc giữa cạnh bên và mặt đáy bằng 60 ° . Tính thể tích của khối chóp SABC
A. a 3 3 12
B. a 3 12
C. a 3 3 4
D. a 3 3 36
