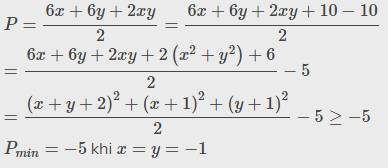biết rằng các số x,y thõa mãn điều kiện x+y=1. tìm giá trị nhỏ nhất của biểu thức C=\(x^2+y^2+xy\)

Những câu hỏi liên quan
Cho x,y là các số thỏa mãn điều kiện x+y = 1. Tìm giá trị nhỏ nhất của biểu thức C = \(x^2+y^2+xy\)
\(C=x^2+y^2+xy\)
\(=\left(x^2+y^2+2xy\right)-xy\)
\(=\left(x+y\right)^2-x\left(1-x\right)\)
\(=1-x+x^2\)
\(=x^2-2\cdot\frac{1}{2}\cdot x+\frac{1}{4}+\frac{3}{4}\)
\(=\left(x-\frac{1}{2}\right)^2+\frac{3}{4}\ge\frac{3}{4}\forall x\)
Dấu "=" xảy ra \(x=y=\frac{1}{2}\)
Vậy \(C_{min}=\frac{3}{4}\) tại \(x=y=\frac{1}{2}\)
Đúng 0
Bình luận (0)
C=(x+y)^2-xy=1-xy
Mà xy<=(x+y)^2/4=1/a suy ra C>=1-1/4=3/4
Dấu = xảy ra khi x=y=1/2
Đúng 0
Bình luận (0)
biết rằng các số x,y thỏa mãn điều kiện x+y=1.Tìm giá trị nhỏ nhất của biểu thức C=x^2+y^2+xy
anh chị nào biết giúp em với ạ,em cảm ơn nhiềuu
\(x+y=1\Rightarrow x=1-y\)
\(C=x^2+y^2+xy=\left(1-y\right)^2+y^2+\left(1-y\right)y\)
\(=y^2-y+1\)\(=\left(y-\dfrac{1}{2}\right)^2+\dfrac{3}{4}\ge\dfrac{3}{4}\forall y\)
=>minC=\(\dfrac{3}{4}\) \(\Leftrightarrow y=\dfrac{1}{2}\Rightarrow x=\dfrac{1}{2}\)
Đúng 2
Bình luận (1)
Ta có :
\(x+y=1\Rightarrow\left(x+y\right)^2=1\)
\(\Leftrightarrow x^2+2xy+y^2=1\)
\(\Leftrightarrow x^2+xy+y^2=1-xy\ge1-\left(\dfrac{x+y}{2}\right)^2=1-\dfrac{1}{4}=\dfrac{3}{4}\)
Hay \(C \ge \dfrac{3}{4}\)
Dấu "=" xảy ra khi \(x=y=\dfrac{1}{2}\)
Đúng 1
Bình luận (0)
cho các số thực x và y thỏa mãn điều kiện \(x^2+y^2=2\)
tìm giá trị nhỏ nhất của biểu thức P=3(x+y)+xy
Cho các số thực x và y thoả mãn điều kiện x^2+y^2=2. tìm giá trị nhỏ nhất của biểu thức P=3(x+y)+xy
\(P=\dfrac{6x+6y+2xy}{2}=\dfrac{6x+6y+2xy+10-10}{2}\)
\(=\dfrac{6x+6y+2xy+2\left(x^2+y^2\right)+6}{2}-5\)
\(=\dfrac{\left(x+y+2\right)^2+\left(x+1\right)^2+\left(y+1\right)^2}{2}-5\ge-5\)
\(P_{min}=-5\) khi \(x=y=-1\)
Đúng 1
Bình luận (3)
cho các số thực x và y thỏa mãn điều kiện x^2 + y^2 = 2 Tìm giá trị nhỏ nhất của biểu thức P = 3(x+y)+xy
cho các số thực x và y thoả mãn điều kiện x^2+y^2=2. tìm giá trị nhỏ nhất của biểu thức P= 3(x+y)+xy
tìm giá trị lớn nhất và giá trị nhỏ nhất của biểu thức B=x+y+z. Biết rằng x,y,z là các số thực thỏa mãn điều kiện y^2+yz+z^2=1007-(3x^2)/2
Cho hai số thực x, y dương thõa mãn điều kiện x2 + y2 - xy = 4. Tìm giá trị lớn nhất và giá trị nhỏ nhất của biểu thức : P = x2 + y2. (Trích đề thi HSG toán 9 tỉnh Bình Định năm học 2012-2013)
tìm giá trị lớn nhất và nhỏ nhất của biểu thức B=x+y+z biết rằng x,y,z là các số thỏa mãn điều kiện y^2+yz+z^2= 2- 3x^2/2
Từ đk trên ta có: \(2y^2+2zy+2z^2=2-3x^2\)
<=> \(3x^2+2y^2+2zy+2z^2=2\left(1\right)\)
<=>\(\left(x+y+z\right)^2+\left(x-y\right)^2+\left(x-z\right)^2=2\)
Do (x-y)2≥0; (x-z)2≥0 nên từ(*) suy ra (x+y+z)2≤2
Hay \(-\sqrt{2}\le x+y+z\le\sqrt{2}\)
Dấu "=" xảy ra khi x-y =0 và x-z=0 hay x=y=z
Thay vào (1) ta được 9x2=2 ; x=\(\dfrac{\sqrt{2}}{3};\dfrac{-\sqrt{2}}{3}\)
Với x=y=z =x=\(\dfrac{\sqrt{2}}{3};\dfrac{-\sqrt{2}}{3}\)thì max=\(\sqrt{2}\), min =\(-\sqrt{2}\)
Đúng 1
Bình luận (0)
Bài 1:Tìm giá trị lớn nhất và giá trị nhỏ nhất của biểu thức P=x^2+y^2/x^2+xy+4y^2 với x2+xy+4y^2 khác 0.Bài 2:Với x;y thỏa mãn điều kiện x^2+y^2=1.Tìm giá trị lớn nhất và giá trị nhỏ nhất của biểu thức P=2(xy+y^2)/1+2x^2+2xy.Giúp mik nhé mai mik đi hc r