Lời giải:

a.

Đồ thị xanh lá: $y=2x+1$
Đồ thị xanh dương: $y=x-3$
b.

PT hoành độ giao điểm:
$y=2x+1=x-3$
$\Leftrightarrow x=-4$

$y=x-3=(-4)-3=-7$
Vậy tọa độ điểm $M$ là $(-4;-7)$

a) vẽ đồ thị của hàm số \(y=-x\)

đồ thị hàm số \(y=-x\)là 1 đường thẳng đi qua gốc tọa độ \(O\left(0;0\right)\)và 1 điểm \(A\left(1;-1\right)\)

b) 

a) vẽ bạn tự vẽ nha

b) Xét pt hoành độ giao điểm chung của (d) và (P) ta có:
\(\frac{1}{4}x^2=x+m\)

\(\Leftrightarrow x^2-4x-4m=0\left(1\right)\)

\(\Delta^,=4+4m\)

Để (d) tiếp xúc với (P) \(\Leftrightarrow\Delta^,=0\)

\(\Leftrightarrow4+4m=0\)

\(\Leftrightarrow m=-1\)

Thay m=-1 vào pt (1) ta được : 

\(x^2-4x+4=0\)

\(\Leftrightarrow\left(x-2\right)^2=0\)

\(\Leftrightarrow x=2\)

\(\Rightarrow y=\frac{1}{4}.2^2=1\)

Gọi tọa độ tiếp điểm của (d) tiếp xúc với (P) là A(x,y) 

=> tọa độ tiếp điểm là \(A\left(2;1\right)\)

a) Đồ thị:

b) Gọi giao điểm của đồ thị của hàm số y = x - 1 với trục tung, với trục hoành lần lượt là 2 điểm B và C

Thay x = 0 vào hàm số y = x - 1 ta có:

y = 0 - 1 = - 1

⇒ B(0; -1)

Thay y = 0 vào hàm số y = x - 1 ta có:

x - 1 = 0

⇔ x = 1

⇒ C(1; 0)

c) Gọi (t): y = ax + b (a 0)

Do (t) // (d) nên a = -2

⇒ (t): y = -2x + b

Thay y = -3 vào (d') ta có:

x - 1 = -3

⇔ x = -3 + 1

⇔ x = -2

Thay x = -2; y = -3 vào (t) ta có:

-2.(-2) + b = -3

⇔ 4 + b = -3

⇔ b = -3 - 4

⇔ b = -7

Vậy (t): y = -2x - 7

\(a,-1< 0\Leftrightarrow\left(d'\right)\text{ nghịch biến trên }R\\ b,\text{PT hoành độ giao điểm: }x=-x+2\Leftrightarrow x=1\Leftrightarrow y=1\Leftrightarrow A\left(1;1\right)\\ \text{Vậy }A\left(1;1\right)\text{ là giao 2 đths}\\ c,\text{3 đt đồng quy }\Leftrightarrow A\left(1;1\right)\in\left(d''\right)\\ \Leftrightarrow m-1+2m=1\\ \Leftrightarrow3m=2\Leftrightarrow m=\dfrac{2}{3}\)

a: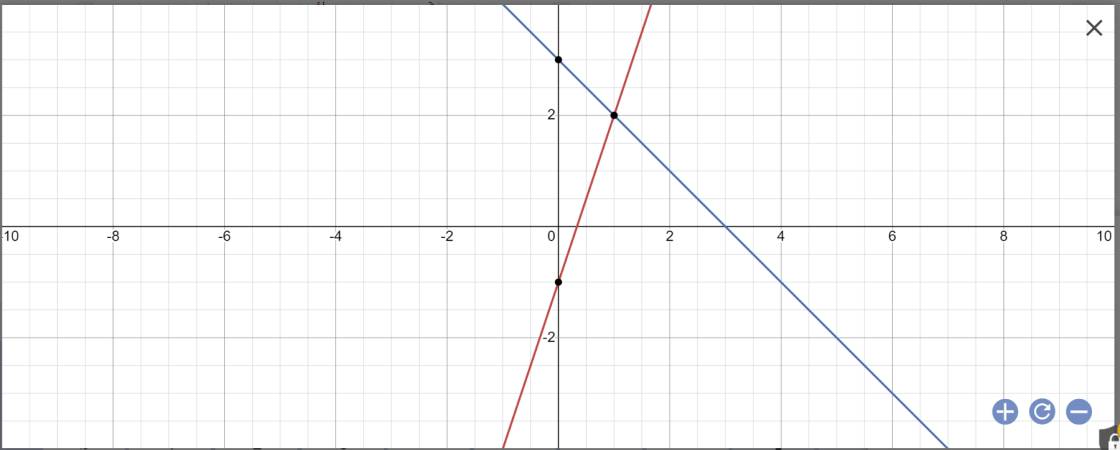 

b: Tọa độ A là:

\(\left\{{}\begin{matrix}y=0\\3x-1=0\end{matrix}\right.\)

=>\(\left\{{}\begin{matrix}x=\dfrac{1}{3}\\y=0\end{matrix}\right.\)

Vậy: A(1/3;0)

Tọa độ B là:

\(\left\{{}\begin{matrix}y=0\\-x+3=0\end{matrix}\right.\)

=>\(\left\{{}\begin{matrix}y=0\\-x=-3\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}y=0\\x=3\end{matrix}\right.\)

Vậy: B(3;0)

Tọa độ C là:

\(\left\{{}\begin{matrix}3x-1=-x+3\\y=3x-1\end{matrix}\right.\)

=>\(\left\{{}\begin{matrix}4x=4\\y=3x-1\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=1\\y=3\cdot1-1=2\end{matrix}\right.\)

Vậy: C(1;2)

c: Gọi \(\alpha\) là góc tạo bởi (d1) với trục Ox

\(tan\alpha=a=3\)

=>\(\alpha\simeq71^033'\)

b: Tọa độ M là:

x=0 và y=1-3/2*0=1

Vì (d) đi qua M(0;1) và N(2;3) nên ta có hệ:

0a+b=1 và 2a+b=3

=>b=1; a=1

a, Thay x = -2 => y = -2 + 4 = 2 => A(-2;2) 

(d) cắt y = x + 4 tại A(-2;2) <=> 2 = -2 ( m + 1 ) - 2 

<=> -2m - 2 - 2 = 2 <=> -2m = 6 <=> m = -3 

Vậy (d) : y = -2x - 2 

b, bạn tự vẽ nhé 

c, Cho x = 0 => y = -2 

=> (d) cắt trục Oy tại A(0;-2) => OA = | -2 | = 2 

Cho y = 0 => x = -1 

=> (d) cắt trục Ox tại B(-1;0) => OB = | -1 | = 1 

Ta có : \(S_{OAB}=\frac{1}{2}.OA.OB=\frac{1}{2}.2.1=1\)( dvdt ) 

Đặt:  (d):  y = (m+5)x + 2m - 10

Để y là hàm số bậc nhất thì:  m + 5 # 0    <=>   m # -5

Để y là hàm số đồng biến thì: m + 5 > 0  <=>  m > -5

(d) đi qua A(2,3) nên ta có:

3 = (m+5).2 + 2m - 10

<=>  2m + 10 + 2m - 10 = 3

<=>  4m = 3

<=> m = 3/4

(d) cắt trục tung tại điểm có tung độ bằng 9 nên ta có:

9 = (m+5).0 + 2m - 10

<=> 2m - 10 = 9

<=>  2m = 19

<=> m = 19/2

(d) đi qua điểm 10 trên trục hoành nên ta có:

0 = (m+5).10 + 2m - 10

<=> 10m + 50 + 2m - 10 = 0

<=>  12m = -40

<=> m = -10/3

(d) // y = 2x - 1  nên ta có:

\hept{m+5=22m−10≠−1\hept{m+5=22m−10≠−1   <=>   \hept{m=−3m≠92\hept{m=−3m≠92  <=>  m=−3

Giả sử (d) luôn đi qua điểm cố định M(x₀; y₀)

Ta có:  y0=(m+5)x0+2m−10y0=(m+5)x0+2m−10

<=>  mx0+5x0+2m−10−y0=0mx0+5x0+2m−10−y0=0

<=>  m(xo+2)+5x0−y0−10=0m(xo+2)+5x0−y0−10=0

Để M cố định thì:  \hept{x0+2=05x0−y0−10=0\hept{x0+2=05x0−y0−10=0   <=>   \hept{x0=−2y0=−20\hept{x0=−2y0=−20

Vậy...

????????????????