Cho tam giác ABC vuông tại A, \(\widehat{B}=30^0\)
Chứng minh rằng \(AC=\dfrac{1}{2}BC\)
Cho tam giác ABC vuông tại A, có \(\widehat{B}=30^0\) , lấy điểm D thuộc cạnh BC, sao cho \(\widehat{BAD}=15^0\) . Chứng minh rằng:
AC + CD = nửa chu vi tam giác ABC
Bạn làm theo cách này nhé, sẽ ngắn gọn hơn !
Hạ đường cao AH của \(\Delta\)ABC.
Ta có: ^ADH là góc ngoài của \(\Delta\)ADB => ^ADH = ^ABD + ^BAD = 300 + 150 = 450
Xét \(\Delta\)AHD có: ^AHD=900; ^ADH=450 => \(\Delta\)AHD vuông cân tại H => HD = AH.
Dễ thấy: \(\Delta\)AHB là tam giác nửa đều => AH=1/2.AB => HD=1/2.AB
\(\Delta\)AHC cũng là tam giác nửa đều => HC=1/2.AC
=> HD + HC = 1/2 (AB+AC) => CD = (AB+AC)/2
=> AC + CD = AC + (AB+AC)/2. Do \(\Delta\)ABC nửa đều => AC=BC/2
=> AC + CD = BC/2 + (AB+AC)/2 = CABC/2 (đpcm).
Qua D kẻ đường thẳng vuông góc với BC cắt tia CA tại E. DE giao AB ở I
Gọi H và K lần lượt là hình chiếu của A lên CD và DE
Xét \(\Delta\)BID và \(\Delta\)AIE: ^BDI = ^EAI = 900; ^BID = ^AIE (Đối đỉnh)
=> ^DBI = ^AEI hay ^HBA = ^KEA
Ta có: ^HAB + ^HBA =900; ^KAE + ^KEA = 900. Mà ^HBA=^KEA => ^HAB = ^KAE.
Ta thấy: ^ADC là góc ngoài \(\Delta\)BAD => ^ADC = ^BAD + ^ABD = 300 + 150 = 450
Mà ^CDE = 900 = .^CDE= 2.^ADC => DA là phân giác ^CDE
Do H và K là hình chiếu của A lên CD và DE => AH=AK (T/c đường phân giác)
Xét \(\Delta\)AHB và \(\Delta\)AKE: AH=AK; ^AHB = ^AKE =900; ^HAB = ^KAE (cmt)
=> \(\Delta\)AHB = \(\Delta\)AKE (g.c.g) => AB=AE (2 cạnh tương ứng)
Xét \(\Delta\)CDE: ^CDE=900; ^DCE=600 => \(\Delta\)CDE là tam giác nửa đều
= > \(CD=\frac{CE}{2}=\frac{AC+AE}{2}=\frac{AB+AC}{2}\)(Do AB=AE)
\(\Leftrightarrow AC+CD=AC+\frac{AB+AC}{2}\)(1)
Mặt khác \(\Delta\)ABC là tam giác nửa đều => \(AC=\frac{BC}{2}\)(2)
Từ (1) và (2) \(\Rightarrow AC+CD=\frac{BC}{2}+\frac{AB+AC}{2}=\frac{AB+AC+BC}{2}=\frac{C_{\Delta ABC}}{2}\)
=> ĐPCM.
Cho tam giác ABC thỏa mãn điều kiện \(\widehat{A}=2\widehat{B}=4\widehat{C}\)
Chứng minh rằng: \(\dfrac{1}{AB}=\dfrac{1}{AC}+\dfrac{1}{BC}\)
Mọi ngừi vẽ hình và làm hết giùm mk câu này
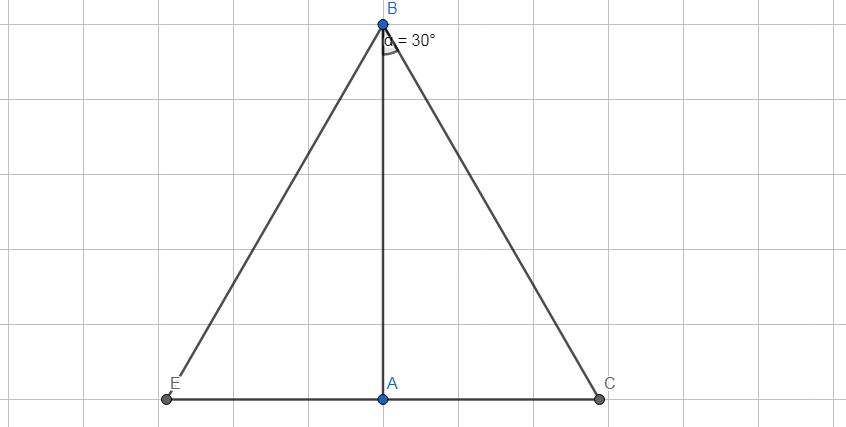
Cho \(\Delta\)\(ABC\) vuông tại A. \(\widehat{B}\) \(=30^0\). Trên tia đối của tia AC lấy điểm E sao cho AE = AC. Chứng minh
a) Tam giác BCE đều
b) \(AC=\dfrac{1}{2}BC\)
a) Xét tam giác ABC vuông tại A có:
\(\widehat{ABC}+\widehat{ACB}=90^0\)(phụ nhau)
=>300+\(\widehat{ACB}\)=900
=>\(\widehat{ACB}\)=600
Xét tam giác BEC có:
BA là đường cao (BA vuông góc với EC tại A)
BA là trung tuyến (A là trung điểm EC)
=>Tam giác BEC cân tại B mà \(\stackrel\frown{BCE}=60^0\)(cmt)
=>Tam giác BEC đều.
b) Ta có: AC=\(\dfrac{1}{2}\)CE mà CE=BC ( tam giác BCE đều)
=>AC=\(\dfrac{1}{2}\)BC
Cho tam giác ABC vuông tại A,biết góc B=30 độ.Chứng minh rằng AC=\(\dfrac{1}{2}\)BC
Với có và
Gọi là trung điểm của
Mà có
( định lý)
cân tại
Mà
đều
Cho tam giác ABC vuông tại A (AB > AC), đường cao AH
a) Chứng minh: \(\dfrac{AB^2}{BH}=\dfrac{AC^2}{CH}\)
b) Biết \(\widehat{C}\) \(=60^0\), AC = 8, AB = 12. Giải tam giác HAB
a: ΔABC vuông tại A có AH là đường cao
nên AB^2=BH*BC; AC^2=CH*CB
=>AB^2/AC^2=BH/CH
b:
góc B=90-60=30 độ
góc HAB=90-30=60 độ
BC=căn 8^2+12^2=4*căn 13(cm)
HB=AB^2/BC=36/căn 13(cm)
AH=8*12/4*căn 13=24/căn 13(cm)
Cho tam giác ABC có\(\widehat{B}=30\) và \(AC=\frac{1}{2}BC\)Chứng minh tam giác abc vuông tại A
Mik xem zồi trên google có đó bn lên đó xem nha!
Với tam giác ABC có góc A = \(90^o\)và góc B = \(30^o\)
=> Góc C = \(60^o\)
Gọi M là trung điểm của BC
Mà \(\Delta ABC\)có góc A = 90\(^o\)
=> AM = BM = CM \((\)định lý \()\)
=> Tam giác AMC cân tại M
Mà góc C = 60\(^o\)
=> \(\Delta ABC\)đều
=> AM = MC
Mà MC = \(\frac{1}{2}\)BC
Vậy : \(AC=\frac{1}{2}BC\)
Mình xin lỗi bạn tự nhiên mk chứng minh \(AC=\frac{1}{2}BC\)
Sorry bạn
cho tam giác ABC vuông tại A,B = 30 độ. Chứng minh rằng AC = 1/2 BC
Với tam giác ABC có góc \(A=90^o\) và góc \(B=30^o\)
=> góc \(C=60^o\)
Gọi M là trung điểm của BC
mà \(\Delta\) ABC có góc \(A=90^o\)
=>AM=BM=CM(định lý)
=>tam giác AMC cân tại M
mà góc \(C=60^o\)
=> \(\Delta\) AMC đều
=>AC=MC
mà MC =1/2.BC
=> AC = 1/2 BC
cho tam giác ABC vuông tại A,B = 30 độ. Chứng minh rằng AC = 1/2 BC
Với tam giác ABC có góc \(A=90^o\) và góc \(B=60^o\)
=> góc \(C=60^o\)
Gọi M là trung điểm của BC
mà tam giác ABC có góc \(A=90^o\)
=>AM=BM=CM(định lý)
=>tam giác AMC cân tại M
mà góc \(C=60^o\)
=> tam giá AMC đều
=>AC=MC
mà MC =1/2.BC
=> AC = 1/2 BC
Tick nha
Cho tam giác ABC vuông tại A, góc B=30° . Chứng minh rằng AC = 1/2 BC.