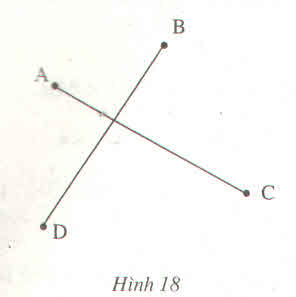
Cho bốn điểm A, B, C, D như trên hình 18. Hãy tìm một điểm M sao cho tổng MA + MB + MC + MD là nhỏ nhất ?
Những câu hỏi liên quan
Cho bốn điểm A, B, C, D như hình bên. Hãy tìm một điểm M sao cho tổng MA + MB + MC + MD là nhỏ nhất.
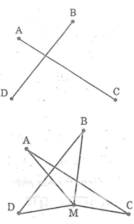
* Nếu M không trùng với giao điểm của AC và BD
Trong ΔAMC, ta có: MA + MC > AC (bất đẳng thức tam giác)
Trong ΔMBD, ta có: MB + MD > BD (bất đẳng thức tam giác)
* Nếu M trùng với giao điểm AC và BD
Ta có: MA + MC = AC
MB + MD = BD
+) Kết hợp cả hai trường hợp, suy ra: MA + MC ≥ AC
Và MB + MD ≥ BD (dấu bằng xảy ra khi M trùng với giao điểm của AC và BD)
Suy ra: MA + MB + MC + MD ≥ AC + BD
Vậy MA + MB + MC + MD = AC + BD bé nhất khi đó M là giao điểm của AC và BD.
Đúng 0
Bình luận (0)
Bài 1: Cho tam giác ABC (AC > AB) và đường trung tuyến AM. Lấy E tuỳ ý trên AM. CMR: góc EBC > ECB.
Bài 2: Cho 4 điểm A, B, C, D như hình vẽ. Hãy tìm 1 điểm M sao cho MA + MB + MC + MD nhỏ nhất.
Cho tam giác nội tiếp đường trong (O) và M là một điểm trên cung nhỏ BC. Trên đoạn MA lấy điểm D sao cho MD=MB
a) Hỏi tam giác MDB là tam giác gì
b) so sánh hai tam giác BDA và BMC
c) Chứng minh MA=MB+MC
d) tìm vị trí của M để MA + MB +MC lớn nhất
cho mihf hỏi tam giác gì nội tiếp đường tròn O vậy
mình nghĩ đề cho bổ sung là cho tam giác ABC đều nội tiếp đường tròn ( O ) vì mình đã từng làm rồi
lời giải :
a) vì MD = MB nên \(\Delta MBD\)cân tại M
\(\widehat{BMD}=\widehat{BCA}=60^o\)( cùng chắn cung AB )
\(\Rightarrow\)\(\Delta MBD\)đều
b) Xét \(\Delta MBC\)và \(\Delta BDA\)có :
MB = BD ; BC = AB ; \(\widehat{MBC}=\widehat{DBA}\)( cùng cộng góc DBC bằng 60 độ )
\(\Rightarrow\Delta MBC=\Delta DBA\left(c.g.c\right)\)suy ra MC = AD
c) Mà MB = MD ( câu a )
nên MC + MB = MD + AD = MA
d) Ta có : MA là dây cung của ( O ; R ) \(\Rightarrow MA\le2R\)
\(\Rightarrow MB+MC+MA=2MA\le4R\)( không đổi )
Dấu " = " xảy ra \(\Leftrightarrow\)MA là đường kính hay M là điểm chính giữa của cung BC
Trong không gian với hệ trục tọa độ Oxyz, cho bốn điểm A(2;-3;7), B(0;4;1), C(3;0;5), D(3;3;3). Gọi M là điểm nằm trên mặt phẳng (Oyz) sao cho biểu thức
M
A
→
+
M
B
→
...
Đọc tiếp
Trong không gian với hệ trục tọa độ Oxyz, cho bốn điểm A(2;-3;7), B(0;4;1), C(3;0;5), D(3;3;3). Gọi M là điểm nằm trên mặt phẳng (Oyz) sao cho biểu thức M A → + M B → + M C → + M D → đạt giá trị nhỏ nhất. Khi đó tọa độ M là
A. M(0; 1; -4)
B. M(2; 1; 0)
C. M(0; 1; -2)
D. M(0; 1; 4)
Đáp án D
Gọi I(a; b; c) thỏa mãn
Khi đó
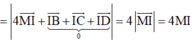
Suy ra MI min => M là hình chiếu của I trên (Oyz) => M(0;1;4)
Đúng 0
Bình luận (0)
Trong không gian Oxyz, cho bốn điểm A (3;1;0), B(2;0;-1), C(0;2;-1), D (0;0;2). Với mỗi điểm M tùy ý, đặt TMA+MB+MC+MD. Gọi
M
∘
a
;
b
;
c
sao cho T đạt giá trị nhỏ nhất. Lúc đó, tổng
a
+
5
b
+
c
bằng A. 3. B. -13. C. 7. D. 4
Đọc tiếp
Trong không gian Oxyz, cho bốn điểm A (3;1;0), B(2;0;-1), C(0;2;-1), D (0;0;2). Với mỗi điểm M tùy ý, đặt T=MA+MB+MC+MD. Gọi M ∘ a ; b ; c sao cho T đạt giá trị nhỏ nhất. Lúc đó, tổng a + 5 b + c bằng
A. 3.
B. -13.
C. 7.
D. 4
Trong không gian với hệ trục tọa độ Oxyz, cho bốn điểm A(2;-3;7), B(0;4;1), C(3;0;5) và D(3;3;3). Gọi M là điểm nằm trên mặt phẳng (Oyz) sao cho biểu thức
M
A
→
+
M
B
→
+
M
C
→...
Đọc tiếp
Trong không gian với hệ trục tọa độ Oxyz, cho bốn điểm A(2;-3;7), B(0;4;1), C(3;0;5) và D(3;3;3). Gọi M là điểm nằm trên mặt phẳng (Oyz) sao cho biểu thức M A → + M B → + M C → + M D → đạt giá trị nhỏ nhất. Khi đó tọa độ của M là:
A. M (0;1;-4)
B. M (2;1;0)
C. M (0;1;-2)
D. M (0;1;4)
Chọn D
Vậy M là hình chiếu vuông góc của G lên mặt phẳng (Oyz) nên M (0;1;4)
Đúng 0
Bình luận (0)
Trong không gian Oxyz, cho bốn điểm A ( 2;0;0 ), B ( 0;4;0 ), C ( 0;0;6 ), D ( 2;4;6 ). Xét các mệnh đề sau:(I). Tập hợp các điểm M sao cho
M
A
→
+
M
B
→
M
C
→
+
M...
Đọc tiếp
Trong không gian Oxyz, cho bốn điểm A ( 2;0;0 ), B ( 0;4;0 ), C ( 0;0;6 ), D ( 2;4;6 ). Xét các mệnh đề sau:
(I). Tập hợp các điểm M sao cho M A → + M B → = M C → + M D → là một mặt phẳng
(II). Tập hợp các điểm M sao cho M A → + M B → + M C → + M D → = 4 là một mặt cầu tâm I(1;2;3) và bán kính R = 1
A. Chỉ (I)
B. Chỉ (II)
C. Không có
D. Cả (I) cả (II)
Xét mệnh đề (I):
Gọi I, J lần lượt là trung điểm AB, CD. Khi đó
M A → + M B → = M C → + M D → ⇔ 2 M I → = 2 M J → ⇔ M I = M J
Do đó tập hợp các điểm M là mặt phẳng trung trực của IJ
Vậy mệnh đề này đúng.
* Xét mệnh đề (II):
Gọi G là trọng tâm tứ diện ABCD
Khi đó M A → + M B → + M C → + M D → = 4 ⇔ 4 M G → = 4 ⇔ M G = 1
Do đó tập hợp các điểm M là mặt cầu tâm G ( 1;2;3 ) và bán kính R = 1
Vậy mệnh đề này đúng
Đáp án D
Đúng 0
Bình luận (0)
1.Cho bốn điểm A,B,C,D thẳng hàng theo thứ tự đó sao cho AB=CD.CM với mọi điểm M nằm trong mặt phẳng MA+MD lớn hơn hoặc bằng MB+MC
2.Cho hình bình hành ABCD và một điểm M.CM 4 đường thẳng vẽ qua A,B,C,D lần lượt song song với MC,MD,MA,MB là các đường thẳng đồng quy.
MN GIÚP VỚI MÌNH CẦN GẤP
1.Cho bốn điểm A,B,C,D thẳng hàng theo thứ tự đó sao cho AB=CD.CM với mọi điểm M nằm trong mặt phẳng MA+MD lớn hơn hoặc bằng MB+MC
2.Cho hình bình hành ABCD và một điểm M.CM 4 đường thẳng vẽ qua A,B,C,D lần lượt song song với MC,MD,MA,MB là các đường thẳng đồng quy.
MN GIÚP VỚI MÌNH CẦN GẤP