Cho 4 điểm A,B,C,D.Trong đó không có 3 điểm nào thẳng hàng .Hỏi có bao nhiêu tam giác mà có 3 đỉnh là 3 trong 4 điểm trên.

Những câu hỏi liên quan
Trên mặt phẳng cho 3 điể m trong đó không có ba điểm nào thẳng hàng
a) Hỏi vẽ được bao nhiêu đoạn thẳng có các đầu mút là các điểm đó?
b) Hỏi vẽ được bao nhiêu tam giác có các đỉnh là các điểm đó?
c) Nếu trong đó có 4 điểm thẳng hàng các điểm khác không thẳng hàng thì vẽ được bao nhiêu tam giác?
Cho 10 điểm phân biệt A1, A2, …, A10 trong đó có 4 điểm A1, A2, A3, A4 thẳng hàng, ngoài ra không có 3 điểm nào thẳng hàng. Hỏi có bao nhiêu tam giác có 3 đỉnh được lấy trong 10 điểm trên ? A. 96 tam giác B. 60 tam giác C. 116 tam giác D. 80 tam giác
Đọc tiếp
Cho 10 điểm phân biệt A1, A2, …, A10 trong đó có 4 điểm A1, A2, A3, A4 thẳng hàng, ngoài ra không có 3 điểm nào thẳng hàng. Hỏi có bao nhiêu tam giác có 3 đỉnh được lấy trong 10 điểm trên ?
A. 96 tam giác
B. 60 tam giác
C. 116 tam giác
D. 80 tam giác
Đáp án C
Số cách lấy 3 điểm từ 10 điểm trên là ![]() .
.
Số cách lấy 3 điểm bất kỳ trong 4 điểm A1, A2, A3, A4 là: ![]()
Khi lấy 3 điểm bất kỳ trong 4 điểm A1, A2, A3, A4 thì sẽ không tạo thành tam giác.
![]() Số tam giác tạo thành :
Số tam giác tạo thành : ![]() tam giác.
tam giác.
Đúng 0
Bình luận (0)
Cho 10 điểm phân biệt
A
1
,
A
2
,
.
.
.
.
.
A
10
trong đó có 4 điểm
A
1
,
A
2
,
A
3
,
A
4
thẳng hàng, ngoài ra không có 3 điểm nào thẳng hàng. Hỏi có bao nhiêu tam giác có 3 đỉnh được lấy trong 10 điểm trên? A. 96 tam giác. B. 60 tam...
Đọc tiếp
Cho 10 điểm phân biệt A 1 , A 2 , . . . . . A 10 trong đó có 4 điểm A 1 , A 2 , A 3 , A 4 thẳng hàng, ngoài ra không có 3 điểm nào thẳng hàng. Hỏi có bao nhiêu tam giác có 3 đỉnh được lấy trong 10 điểm trên?
A. 96 tam giác.
B. 60 tam giác.
C. 116 tam giác.
D. 80 tam giác.
Đáp án là C
Số cách lấy 3 điểm từ 10 điểm phân biệt là C 10 3 = 120
Số cách lấy 3 điểm bất kì trong 4 điểm A 1 , A 2 , A 3 , A 4 là C 4 3 = 4
Khi lấy 3 điểm bất kì trong 4 điểm A 1 , A 2 , A 3 , A 4 thì sẽ không tạo thành tam giác.
Như vậy, số tam giác tạo thành : 120- 4 = 116 tam giác.
Đúng 0
Bình luận (0)
Cho 4 điểm A, B, C, D trong đó không có 3 điểm nào thẳng hàng. Tính số tam giác có ba đỉnh là 3 trong 4 điểm trên. Viết tên các tam giác đó.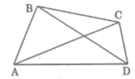
Ta có 4 tam giác: Δ ABC, ΔABD, ΔBCD, ΔACD
Đúng 0
Bình luận (0)
Cho 8 điểm, trong đó không có 3 điểm nào thẳng hàng. Hỏi có bao nhiêu tam giác mà ba đỉnh của nó được chọn từ 8 điểm trên?
A. 336
B. 56
C. 168
D. 84
Đáp án B
Số tam giác tạo thành là C 8 3 = 56
Đúng 0
Bình luận (0)
Cho 8 điểm, trong đó không có 3 điểm nào thẳng hàng. Hỏi có bao nhiêu tam giác mà ba đỉnh của nó được chọn từ 8 điểm trên?
A. 336
B. 56
C. 168
D. 84
Đáp án B
Số tam giác tạo thành là C 8 3 = 56
Đúng 0
Bình luận (0)
Cho 4 điểm A, B, C, D trong đó không có 3 điểm nào thẳng hàng. Tính số tam giác có 3 đỉnh là 3 trong 4 điểm trên. Viết tên các tam giác đó ?
Có bốn tam giác thỏa mãn yêu cầu đề bài, tên các tam giác đó là:
Tam giác ABC, tam giác CAD, tam giác BCD và tam giác ABD
Đúng 0
Bình luận (0)
Ta có 4 tam giác: Δ ABC, ΔABD, ΔBCD, ΔACD
Đúng 0
Bình luận (0)
Cho 5 điểm A; B; C; D; E trong đó không có ba điểm nào thẳng hàng. Có bao nhiêu tam giác có các đỉnh là 3 trong 5 đỉnh trên:
A. 9
B. 10
C. 8
D. 7
Đáp án là B
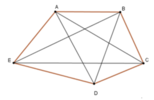
Có 10 tam giác mà các đỉnh là ba trong năm điểm đã cho là:
ΔABC; ΔABD; ΔABE; ΔBCD; ΔBCE; ΔCDA; ΔCDE; ΔDEB; ΔDEA; ΔAEC
Đúng 0
Bình luận (0)
Trong mặt phẳng cho 10 điểm phân biệt
A
1
,
A
2
,
.
.
.
,
A
10
trong đó có 4 điểm
A
1
,
A
2
,
A
3
,
A
4
thẳng hàng, ngoài ra không có 3 điểm nào thẳng hàng. Hỏi có bao...
Đọc tiếp
Trong mặt phẳng cho 10 điểm phân biệt A 1 , A 2 , . . . , A 10 trong đó có 4 điểm A 1 , A 2 , A 3 , A 4 thẳng hàng, ngoài ra không có 3 điểm nào thẳng hàng. Hỏi có bao nhiêu tam giác có 3 đỉnh được lấy trong 10 điểm trên?
A. 116 tam giác
B. 80 tam giác
C. 96 tam giác
D. 60 tam giác
Trong mặt phẳng cho 10 điểm phân biệt A1, A2,...,A10 trong đó có 4 điểm A1, A2, A3, A4 thẳng hàng, ngoài ra không có 3 điểm nào thẳng hàng. Hỏi có bao nhiêu tam giác có 3 đỉnh được lấy trong 10 điểm trên? A. 116 tam giác. B. 80 tam giác. C. 96 tam giác. D. 60 tam giác.
Đọc tiếp
Trong mặt phẳng cho 10 điểm phân biệt A1, A2,...,A10 trong đó có 4 điểm A1, A2, A3, A4 thẳng hàng, ngoài ra không có 3 điểm nào thẳng hàng. Hỏi có bao nhiêu tam giác có 3 đỉnh được lấy trong 10 điểm trên?
A. 116 tam giác.
B. 80 tam giác.
C. 96 tam giác.
D. 60 tam giác.
Đáp án A.
Ta có 3TH.
+) TH1: 2 trong số 4 điểm A1, A2, A3, A4 tạo thành 1 cạnh, suy ra có C 4 2 . 6 = 36 tam giác.
+) TH2: 1 trong số 4 điểm A1, A2, A3, A4 là 1 đỉnh của tam giác, suy ra có 4 C 6 2 = 60 tam giác.
+) TH3: 0 có đỉnh nào trong 4 điểm A1, A2, A3, A4 là đỉnh của tam giác có C 6 3 = 20 tam giác. Suy ra có 36 + 60 + 20 = 116 tam giác có thể lập được.
Đúng 0
Bình luận (0)








