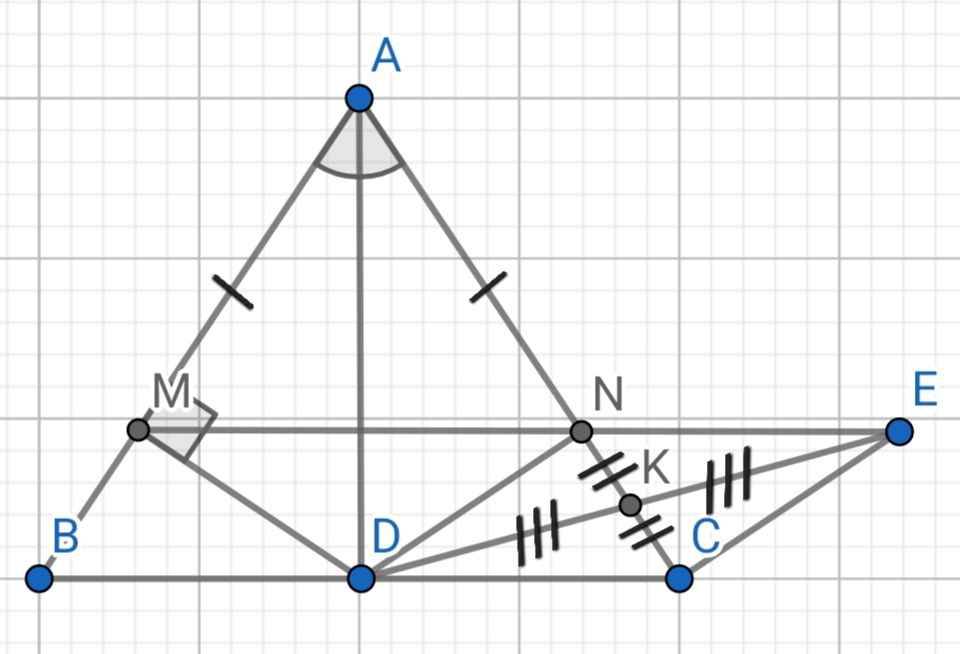
cho tam giác ABC cân tại A kẻ đường cao AD từ D vẽ DM vuông góc với AB tại M và DN vuông góc với AC tại N
a)CM :AD là đường trung tuyến của MN
b)trên tia đối của tia DM lấy một đoạn DE=DM chứng minh CE vuông góc với DE tại E
c)cho BC=10cm bm=3cm tính ME