Cho số phức z = 1-1/3i.tín số phức w=iz liên hợp +3z
A w=10/3+i
Mn giúp em tính kết quả vs
Cho số phức z, biết ( 2 z - 1 ) ( 1 + i ) + ( z ¯ + 1 ) ( 1 - i ) = 2 - 2 i .
Tìm số phức liên hợp của số phức w=3z-3i
A. 1 3 - 1 3 i
B. 1 3 + 1 3 i
C. 1 - 4 i
D. 1 + 4 i
Chọn D.
Giả sử z=a+bi với a,b ∈ ℝ
Thay vào biểu thức ta được:
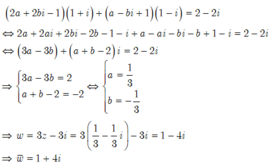
Cho số phức z = 1 - 1 3 i . Tìm số phức w = i z + 3 z được
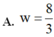
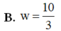
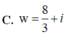
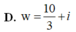
Cho số phức z = 1 − 1 3 i . Tìm số phức w = i z ¯ + 3 z được
A. w = 8 3
B. w = 10 3
C. w = 8 3 + i
D. w = 10 3 + i
Cho số phức z = 1 - 1 3 i . Tìm số phức w = i z ¯ + 3 z được
A. w= 8 3
B. w= 10 3
C. w= 8 3 +i
D. w= 10 3 +i
Đáp án A
Phương pháp: Sử dụng công thức cộng, nhân các số phức.
Cách giải:
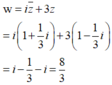
Cho số phức z , biết 2 z - 1 1 + i + z ¯ + 1 1 - i = 2 - 2 i . Tìm số phức liên hợp của số phức w = 3 z - 3 i
A. 1 3 - 1 3 i
B. 1 3 + 1 3 i
C. 1 - 4 i
D. 1 + 4 i
Cho các số phức z thỏa mãn z − i = 5 . Biết rằng tập hợp điểm biểu diễn số phức w = i z + 1 − i là đường tròn. Tính bán kính của đường tròn đó.
A. r = 22
B. r = 10
C. r = 4
D. r = 5
Đáp án là D.
Ta có w + i = i z − i ⇒ w + i = i z − i = 5.
Vậy các điểm biểu diễn số phức w là đường tròn có bán kính r=5
Cho các số phức z thỏa mãn z - i = 5 . Biết rằng tập hợp điểm biểu diễn số phức w = i z + 1 - i là đường tròn. Tính bán kính của đường tròn đó.
A. r = 22
B. r = 10
C. r = 4
D. r = 5
Đáp án là D.
Ta có ![]()
Vậy các điểm biểu diễn số phức w là đường tròn có bán kính r = 5.
Cho các số phức z thỏa mãn | z - i | = 5 . Biết rằng tập hợp điểm biểu diễn số phức w = iz+1-i là đường tròn. Tính bán kính của đường tròn đó.
A. r = 20.
B. r = 5.
C. r = 22.
D. r = 4.
Cho số phức z = (1 - i) ( 2i - 8) . Tìm số phức w = i z + z ¯
A. w = 10 - 10i.
B. w = -3 - 3i.
C. w = 16 - 16i.
D. w = -16 - 16i.
Chọn D.
+ Do z = (1 - i)(2i - 8) = 2i + 2 - 8 + 8i hay z = -6 + 10i
Khi đó:![]() và iz = -10 - 6i
và iz = -10 - 6i
Khi đó: w = ( -10 - 6i) + ( -6 -10i) = -16 - 16i.