Đáp án A
Phương pháp: Sử dụng công thức cộng, nhân các số phức.
Cách giải:
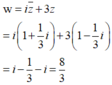
Đáp án A
Phương pháp: Sử dụng công thức cộng, nhân các số phức.
Cách giải:
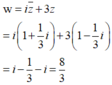
Các số phức z, w thay đổi nhưng thỏa mãn |z + i – 2i| = 1 và |w - 3 + i| = 3. Tìm |z - w|max
A. |z - w|max = 2.
B. |z - w|max = 4.
C. |z - w|max = 9.
D. |z - w|max = 10.
Cho các số phức z và w thỏa mãn ( 3 - i ) | z | = z w - 1 + 1 - i . Tìm GTLN của T = | w + i |
![]()
Xét các số phức z thỏa mãn |z+1+i| = 3.Đặt w = z + 2i -3. Tìm Max |w|
A. Max = 9
B.Max = 8
C. Max = 6
D. Max =5
Xét các số phức z thỏa mãn |z+1+i| = 3.Đặt w = z + 2i -3. Tìm Max |w|
A. Max = 9
B.Max = 8
C. Max = 6
D. Max =5
Cho hai số phức z, w thỏa mãn | z - 3 - 2 i | ≤ 1 | w + 1 + 2 i | ≤ | w - 2 - i | . Tìm gía trị nhỏ nhất P m i n của biểu thức P = |z-w|.
A . P m i n = 3 2 - 2 2
B . P m i n = 2 + 1
C . P m i n = 5 2 - 2 2
D . P m i n = 2 2 + 1 2
Cho số phức z thỏa mãn điều kiện ( 3 + 2 i ) z + ( 2 - i ) 2 = 4 + i . Tìm phần ảo của số phức w = ( 1 + z ) z ¯ .
![]()
![]()
![]()
![]()
Cho số phức z = 3 - 2i. Tìm điểm biểu diễn của số phức w = z + i. z ¯
A. M(1;1)
B. M(1;-5)
C. M(5;-5)
D. M(5;1)
Cho số phức z = 3 - 2i Tìm điểm biểu diễn của số phức w = z + i. z ¯
A. M(1;1)
B. M(1;-5)
C. M(5;-5)
D. M(5;1)
Cho số phức z = (1 - i) ( 2i - 8) . Tìm số phức w = i z + z ¯
A. w = 10 - 10i.
B. w = -3 - 3i.
C. w = 16 - 16i.
D. w = -16 - 16i.
Cho hai số phức w và z thỏa mãn w - 1 + 2 i = z . Biết tập hợp các điểm biểu diễn của số phức z là đường tròn tâm I(-2;3) bán kính r = 3. Tìm tập hợp các điểm biểu diễn của số phức
A. Là một đường thẳng song song trục tung
B. Là một đường thẳng không song song với trục tung
C. Là đường tròn, tọa độ tâm (-3;5) bán kính bằng 3 5
D. Là đường tròn, tọa độ tâm (-1;1) bán kính bằng 3