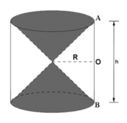
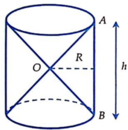
Hình 98 cho ta hình ảnh của một cái đồng hồ cát với các kích thước kèm theo (OA = OB). Hãy so sánh tổng các thể tích của hai hình nón và thể tích của hình trụ.

Những câu hỏi liên quan
Hình 98 cho ta hình ảnh của một cái đồng hồ cát với các kích thước kèm theo (AO = OB).
Hãy so sánh tổng thể tích của hai hình nón và thể tích của hình trụ.
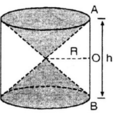
Hình 98
Hình 98 cho ta hình ảnh của một cái đồng hồ cát với các kích thước kèm theo (AO = OB).
Hãy so sánh tổng thể tích của hai hình nón và thể tích của hình trụ.
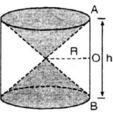
Hình 98
Hình bên cho ta hình ảnh của một đồng hồ cát với các kích thước kèm theo OA OB. Khi đó tỉ số tổng thể tích của hai hình nón
(
V
n
)
và thể tích hình trụ
(
V
t
)
bằng A.
1
2
B.
1
4
C.
2...
Đọc tiếp
Hình bên cho ta hình ảnh của một đồng hồ cát với các kích thước kèm theo OA = OB. Khi đó tỉ số tổng thể tích của hai hình nón ( V n ) và thể tích hình trụ ( V t ) bằng
A. 1 2
B. 1 4
C. 2 5
D. 1 4
Hình bên cho ta hình ảnh của một đồng hồ cát vớicác kích thước kèm theo OAOB .Khi đó tỉ số tổng thể tích của hai hình nón
V
n
và thể tích hình trụ
V
t
bằng A.
1
2
B.
1
4
C.
2
5
D.
1
3
Đọc tiếp
Hình bên cho ta hình ảnh của một đồng hồ cát với
các kích thước kèm theo OA=OB .Khi đó tỉ số tổng
thể tích của hai hình nón V n và thể tích hình trụ
V t bằng
A. 1 2
B. 1 4
C. 2 5
D. 1 3
Hình bên cho ta ảnh của một đồng hồ cát với kích thước kèm theo OAOB. Khi đó tỉ số thể tích của hai hình nón
V
n
và thể tích hình trụ
V
t
bằng A.
1
2
B.
1
4
C.
2
5
D.
1
3
Đọc tiếp
Hình bên cho ta ảnh của một đồng hồ cát với kích thước kèm theo OA=OB. Khi đó tỉ số thể tích của hai hình nón V n và thể tích hình trụ V t bằng
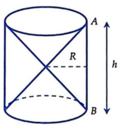
A. 1 2
B. 1 4
C. 2 5
D. 1 3
Hình bên cho ta ảnh của một đồng hồ cát với kích thước kèm theo OA OB. Khi đó tỉ số thể tích của hai hình nón
V
n
và thể tích hình trụ
V
t
bằng:
A
.
1
2
B
.
1
4
C
.
2
5
D...
Đọc tiếp
Hình bên cho ta ảnh của một đồng hồ cát với kích thước kèm theo OA = OB. Khi đó tỉ số thể tích của hai hình nón V n và thể tích hình trụ V t bằng:
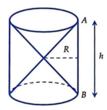
A . 1 2
B . 1 4
C . 2 5
D . 1 3
Đáp án D.
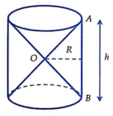
Do OA = OB nên chiều cao của hình nón bằng h 2
Tổng thể tích của 2 hình nón là:
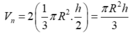
Thể tích hình trụ: 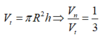
Đúng 0
Bình luận (0)
Hình 120 mô tả một hình cầu được đặt khít vào trong một hình trụ, các kích thước cho trên hình vẽ.Hãy tính:a) Thể tích hình cầu.b) Thể tích hình trụ.c) Hiệu giữa thể tích hình trụ và thể tích hình cầu.d) Thể tích của một hình nón có bán kính đường tròn đáy là r cm và chiều cao 2r cm.e) Từ các kết quả a), b), c), d) hãy tìm mối liên hệ giữa chúng.Hình 120
Đọc tiếp
Hình 120 mô tả một hình cầu được đặt khít vào trong một hình trụ, các kích thước cho trên hình vẽ.
Hãy tính:
a) Thể tích hình cầu.
b) Thể tích hình trụ.
c) Hiệu giữa thể tích hình trụ và thể tích hình cầu.
d) Thể tích của một hình nón có bán kính đường tròn đáy là r cm và chiều cao 2r cm.
e) Từ các kết quả a), b), c), d) hãy tìm mối liên hệ giữa chúng.
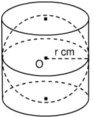
Hình 120
a) Hình cầu bán kính r, vậy thể tích của nó là 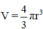
b) Hình trụ có bán kính đáy bằng r và chiều cao bằng 2r
Vậy thể tích của nó là: V 1 = π r 2 ⋅ 2 r = 2 π r 3
c) Thể tích hình trụ trừ đi thể tích hình cầu là:
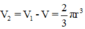
d) Thể tích hình nón có bán kính đáy r, chiều cao 2r
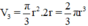
e) Từ các kết quả trên suy ra: Thể tích hình nón "nội tiếp" trong một hình trụ thì bằng thể tích hình trụ trừ đi thể tích hình cầu nội tiếp trong hình trụ ấy.
Hoặc: Thể tích hình trụ bằng tổng thể tích hình nón và hình cầu nội tiếp hình trụ.
Đúng 0
Bình luận (0)
Một cái bồn chứa xăng gồm hai nửa hình cầu và một hình trụ (h.110).
Hãy tính thể tích của bồn chứa theo các kích thước cho trên hình vẽ.
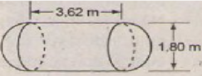
Hình 110
Thể tích cần tính gồm một hình trụ và hai nửa hình cầu.
- Hình cầu có đường kính d = 1,8m ⇒ bán kính R = 0,9m
- Hình trụ có bán kính đáy bằng bán kính hình cầu R = 0,9m; chiều cao h = 3,62m.
Thể tích hình trụ: V 1 = π ⋅ R 2 ⋅ h ≈ 9 , 21 m 3
Thể tích hai nửa hình cầu: V 2 = 4 3 π ⋅ R 3 ≈ 3 , 05 m 3
Thể tích bồn chứa xăng: V = V 1 + V 2 ≈ 12 , 26 m 3
Đúng 0
Bình luận (0)
Một cái bồn chứa xăng gồm hai nửa hình cầu và một hình trụ (h.110).
Hãy tính thể tích của bồn chứa theo các kích thước cho trên hình vẽ.
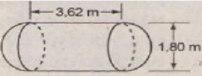
Hình 110
Thể tích cần tính gồm một hình trụ và hai nửa hình cầu.
- Hình cầu có đường kính d = 1,8m ⇒ bán kính R = 0,9m
- Hình trụ có bán kính đáy bằng bán kính hình cầu R = 0,9m; chiều cao h = 3,62m.
Thể tích hình trụ: V1 = π.R2.h ≈ 9,21 (m3).
Thể tích hai nửa hình cầu: 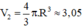 (m3).
(m3).
Thể tích bồn chứa xăng: V = V1 + V2 ≈ 12,26(m3).
Đúng 0
Bình luận (0)
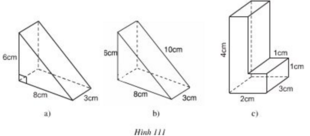
Các hình a, b, c (h.111) gồm một hoặc nhiều lăng trụ đứng. Hãy tính thể tích và diện tích toàn phần của chúng theo các kích thước đã cho trên hình.