Các câu hỏi tương tự
Cho một đồng hồ cát như hình bên dưới (gồm 2 hình nón chung đỉnh ghép lại), trong đó đường sinh bất kỳ của hình nón tạo với đáy một góc
60
°
. Biết rằng chiều cao của đồng hồ là 30cm và tổng thể tích của đồng hồ là
1000
π
c
m
3
.
Hỏi nếu cho đầy lương cát vào phân trên thì chảy hết xuống dưới, khi đó tỷ lệ thể tích lượng cát chiếm chỗ vào thể tích phần phía dưới là bao nhiêu? A. ...
Đọc tiếp
Cho một đồng hồ cát như hình bên dưới (gồm 2 hình nón chung đỉnh ghép lại), trong đó đường sinh bất kỳ của hình nón tạo với đáy một góc 60 ° . Biết rằng chiều cao của đồng hồ là 30cm và tổng thể tích của đồng hồ là 1000 π c m 3 . Hỏi nếu cho đầy lương cát vào phân trên thì chảy hết xuống dưới, khi đó tỷ lệ thể tích lượng cát chiếm chỗ vào thể tích phần phía dưới là bao nhiêu?
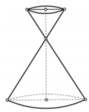
A. 1 3 3
B. 1 8
C. 1 64
D. 1 27
Từ một tấm tôn hình chữ nhật kích thước 50cm x 240cm, người ta làm các thùng đựng nước hình trụ có chiều cao bằng 50cm, theo hai cách sau (xem hình minh họa dưới đây):* Cách 1: Gò tấm tôn ban đầu thành mặt xung quanh của thùng.* Cách 2: Cắt tấm tôn ban đầu thành hai tấm tôn bằng nhau, rồi gò mỗi tấm đó thành mặt xung quanh của một thùng. Kí hiệu
V
1
là thể tích của thùng gò được theo cách 1 và
V
2
là tổng thể tích của hai thùn...
Đọc tiếp
Từ một tấm tôn hình chữ nhật kích thước 50cm x 240cm, người ta làm các thùng đựng nước hình trụ có chiều cao bằng 50cm, theo hai cách sau (xem hình minh họa dưới đây):
* Cách 1: Gò tấm tôn ban đầu thành mặt xung quanh của thùng.
* Cách 2: Cắt tấm tôn ban đầu thành hai tấm tôn bằng nhau, rồi gò mỗi tấm đó thành mặt xung quanh của một thùng. Kí hiệu V 1 là thể tích của thùng gò được theo cách 1 và V 2 là tổng thể tích của hai thùng gò được theo cách 2. Tính tỉ số V 1 V 2
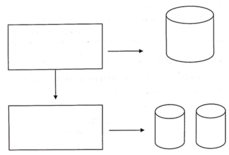
A. V 1 V 2 = 1 2
B. V 1 V 2 = 1
C. V 1 V 2 = 2
D. V 1 V 2 = 2
Một xưởng sản xuất muốn tạo ra những chiếc đồng hồ cát thủy tinh có dạng hình trụ, phần chứa cát là hai nửa hình cầu bằng nhau. Hình vẽ bên với kích thước đã cho là bản thiết kê diện qua trục của chiếc đồng hồ này (phần giới hạn bởi hình trụ và phần hai nửa hình cầu chứa cát). Khi đó, lượng thủy tinh làm chiếc đồng hồcát gần nhất với giá trị nào trong các giá trị sau: A. 1070,8
c
m
3
B. 602,2
c...
Đọc tiếp
Một xưởng sản xuất muốn tạo ra những chiếc đồng hồ cát thủy tinh có dạng hình trụ, phần chứa cát là hai nửa hình cầu bằng nhau. Hình vẽ bên với kích thước đã cho là bản thiết kê diện qua trục của chiếc đồng hồ này (phần giới hạn bởi hình trụ và phần hai nửa hình cầu chứa cát). Khi đó, lượng thủy tinh làm chiếc đồng hồcát gần nhất với giá trị nào trong các giá trị sau:
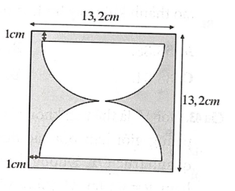
A. 1070,8 c m 3
B. 602,2 c m 3
C. 711,6 c m 3
D. 6021,3 c m 3
Từ một tấm tôn có kích thước 1mx2m, người ta làm ra chiếc thùng đựng nước theo hai cách (xem hình minh họa dưới đây)– Cách 1: làm ra thùng hình trụ có chiều cao 1m, bằng cách gò tấm tôn ban đầu thành mặt xung quanh của thùng. - Cách 2: làm ra thùng hình hộp chữ nhật có chiều cao 1m, bằng cách chia tấm tôn ra thành 4 phần rồi gò thành các mặt bên của hình hộp chữ nhật. Kí hiệu
V
1
là thể tích của thùng được gò theo cách 1 và
V
2...
Đọc tiếp
Từ một tấm tôn có kích thước 1mx2m, người ta làm ra chiếc thùng đựng nước theo hai cách (xem hình minh họa dưới đây)
– Cách 1: làm ra thùng hình trụ có chiều cao 1m, bằng cách gò tấm tôn ban đầu thành mặt xung quanh của thùng.
- Cách 2: làm ra thùng hình hộp chữ nhật có chiều cao 1m, bằng cách chia tấm tôn ra thành 4 phần rồi gò thành các mặt bên của hình hộp chữ nhật. Kí hiệu V 1 là thể tích của thùng được gò theo cách 1 và V 2 là thể tích của thùng được gò theo cách 2. Tính tỷ số V 1 V 2 .
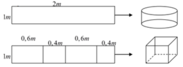
A. V 1 V 2 = 1 0 , 24 π
B. V 1 V 2 = 1 0 , 27 π
C. V 1 V 2 = 1 0 , 7 π
D. V 1 V 2 = 1 0 , 2 π
Cho tấm tôn hình nón có bán kính đáy là
r
2
3
,
độ dài đường sinh l 2. Người ta cắt theo một đường sinh và trải phẳng ra được một hình quạt. Gọi M, N thứ tự là trung điểm OA và OB. Hỏi khi cắt hình quạt theo hình chữ nhật MNPQ (hình vẽ) và tạo thành hình trụ đường sinh PN trùng MQ (2 đáy làm riêng) thì được khối trụ có thể tích bằng bao nhiêu? A.
3
π...
Đọc tiếp
Cho tấm tôn hình nón có bán kính đáy là r = 2 3 , độ dài đường sinh l = 2. Người ta cắt theo một đường sinh và trải phẳng ra được một hình quạt. Gọi M, N thứ tự là trung điểm OA và OB. Hỏi khi cắt hình quạt theo hình chữ nhật MNPQ (hình vẽ) và tạo thành hình trụ đường sinh PN trùng MQ (2 đáy làm riêng) thì được khối trụ có thể tích bằng bao nhiêu?
A. 3 π 13 − 1 8
B. 3 13 − 1 4 π
C. 5 13 − 1 12 π
D. π 13 − 1 9
Một xưởng sản xuất muốn tạo ra những chiếc đồng hồ cát bằng thủy tinh có dạng hình trụ, phần chứa cát là hai nửa hình cầu bằng nhau. Hình vẽ bên với các kích thước đã cho là bản thiết kế thiết diện qua trục của chiếc đồng hồ này (phần tô màu làm bằng thủy tinh). Khi đó, lượng thủy tinh làm chiếc đồng hồ cát gần nhất với giá trị nào trong các giá trị sau A. 711,6
c
m
3
B. 1070,8
c
m
3...
Đọc tiếp
Một xưởng sản xuất muốn tạo ra những chiếc đồng hồ cát bằng thủy tinh có dạng hình trụ, phần chứa cát là hai nửa hình cầu bằng nhau. Hình vẽ bên với các kích thước đã cho là bản thiết kế thiết diện qua trục của chiếc đồng hồ này (phần tô màu làm bằng thủy tinh). Khi đó, lượng thủy tinh làm chiếc đồng hồ cát gần nhất với giá trị nào trong các giá trị sau
A. 711,6 c m 3
B. 1070,8 c m 3
C. 602,2 c m 3
D. 6021,3 c m 3
Từ một tấm tôn có kích thước 1m x 2m, người ta làm ra chiếc thùng đựng nước theo hai cách- Cách 1. Làm ra thùng hình trụ có chiều cao 1m, bằng cách gò tấm tôn ban đầu thành mặt xung quanh của thùng.- Cách 2. Làm ra thùng hình hộp chữ nhật có chiều cao 1m, bằng cách chia tấm tôn ra thành 4 phần rồi gò thành các mặt bên của hình hộp chữ nhật.( xem hình minh họa dưới đây)Kí hiệu
V
1
là thể tích của thùng được gò theo cách 1 và
V...
Đọc tiếp
Từ một tấm tôn có kích thước 1m x 2m, người ta làm ra chiếc thùng đựng nước theo hai cách
- Cách 1. Làm ra thùng hình trụ có chiều cao 1m, bằng cách gò tấm tôn ban đầu thành mặt xung quanh của thùng.
- Cách 2. Làm ra thùng hình hộp chữ nhật có chiều cao 1m, bằng cách chia tấm tôn ra thành 4 phần rồi gò thành các mặt bên của hình hộp chữ nhật.
( xem hình minh họa dưới đây)
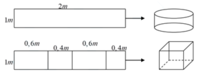
Kí hiệu V 1 là thể tích của thùng được gò theo cách 1 và V 2 là thể tích của thùng được gò theo cách 2. Tỷ số V 1 V 2 bằng
A. 1 0 , 24 π
B. 1 0 , 27 π
C. 1 0 , 7 π
D. 1 0 , 2 π
Cho hình nón (N) có bán kính r 20(cm), chiều cao h 60(cm) và mọt hình trụ (T) nội tiếp hình nón (N) (hình trụ (T) có một đáy thuộc đáy hình nón và một đáy nằm trên mặt xung quanh của hình nón). Tính thể tích V của hình trụ (T) có diện tích xung quanh lớn nhất? A. V3000
π
(
cm
3
)
. B. V
32000
9...
Đọc tiếp
Cho hình nón (N) có bán kính r = 20(cm), chiều cao h = 60(cm) và mọt hình trụ (T) nội tiếp hình nón (N) (hình trụ (T) có một đáy thuộc đáy hình nón và một đáy nằm trên mặt xung quanh của hình nón). Tính thể tích V của hình trụ (T) có diện tích xung quanh lớn nhất?
A. V=3000 π ( cm 3 ) .
B. V= 32000 9 π ( cm 3 ) .
C. V=3600 π ( cm 3 ) .
D. V=4000 π ( cm 3 ) .
Cho hình trụ có hai đáy là hai hình tròn tâm O và O, bán kính đáy bằng r và một hình nón có đỉnh là O đáy là hình tròn tâm O. Biết diện tích xung quanh của hình nón bằng hai lần diện tích đáy của nó. Tính thể tích V của khối trụ giới hạn bởi hình trụ đã cho. A.
V
4
πr
3
3
B.
V
2
πr
3
3
C.
V...
Đọc tiếp
Cho hình trụ có hai đáy là hai hình tròn tâm O và O', bán kính đáy bằng r và một hình nón có đỉnh là O đáy là hình tròn tâm O'. Biết diện tích xung quanh của hình nón bằng hai lần diện tích đáy của nó. Tính thể tích V của khối trụ giới hạn bởi hình trụ đã cho.
A. V = 4 πr 3 3
B. V = 2 πr 3 3
C. V = 3 πr 3 3
D. V = πr 3 3




