đường trung trực d của đoạn thẳng ab chia mặt phẳng thành 2 phần cho điểm m thuộc phần 1 điểm n thuộc phần 2
cmr ma<mb
na>nb
Những câu hỏi liên quan
Đường trung trực d của đoạn thẳng AB chia mặt phẳng thành hai phần I và II như hình dưới. Cho điểm M thuộc phần I và điểm N thuộc phần II. Chứng minh rằng: MA < MB
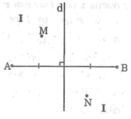
Nối MA, MB
Gọi C là giao điểm của MB với đường thẳng d, nối CA
Ta có: MB = MC + CB
Mà CA = CB (tính chất đường trung trực)
Suy ra: MB = MC + CA (1)
Trong ΔMAC, ta có:
MA < MC + CA (bất đẳng thức tam giác) (2)
Từ (1) và (2) suy ra: MA < MB
Đúng 0
Bình luận (0)
Đường trung trực d của đoạn thẳng AB chia mặt phẳng thành hai phần I và II như hình dưới. Cho điểm M thuộc phần I và điểm N thuộc phần II. Chứng minh rằng: NA > NB
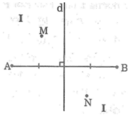
Nối NA, NB. Gọi D là giao điểm của NA với đường thẳng d, nối DB
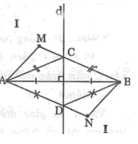
Ta có: NA = ND + DA
Mà DA = DB (tính chất đường trung trực)
Suy ra: NA = ND + DB (3)
Trong ΔNDB, ta có: NB < ND + DB
(bất đẳng thức tam giác) (4)
Từ (3) và (4) suy ra: NA > NB.
Đúng 0
Bình luận (0)
Đường trung trực d của đoạn thẳng AB chia mặt phẳng thành hai phần (không kể đường thẳng d): phần chứa điểm A ký hiệu là PA, phần chứa điểm B ký hiệu là PB (hình bên). Gọi N là một điểm của PB. Chứng minh rằng NB NA
Đọc tiếp
Đường trung trực d của đoạn thẳng AB chia mặt phẳng thành hai phần (không kể đường thẳng d): phần chứa điểm A ký hiệu là PA, phần chứa điểm B ký hiệu là PB (hình bên). Gọi N là một điểm của PB. Chứng minh rằng NB < NA
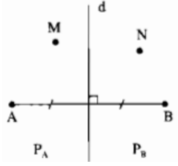
Nối NA, NB. Gọi D là giao điểm của NA với đường thẳng d, nối DB.
Ta có: NA = ND + DA
mà DA = DB (tính chất đường trung trực)
Suy ra: NA = ND + DB (3)
Trong ΔNDB, ta có:
NB < ND + DB (bất đẳng thức tam giác) (4)
Từ (3) và (4) suy ra: NA > NB
Đúng 0
Bình luận (0)
Đường trung trực d của đoạn thẳng AB chia mặt phẳng thành hai phần (không kể đường thẳng d): phần chứa điểm A ký hiệu là PA, phần chứa điểm B ký hiệu là PB (hình bên). Gọi M là một điểm của PA. Chứng minh rằng MA MB
Đọc tiếp
Đường trung trực d của đoạn thẳng AB chia mặt phẳng thành hai phần (không kể đường thẳng d): phần chứa điểm A ký hiệu là PA, phần chứa điểm B ký hiệu là PB (hình bên). Gọi M là một điểm của PA. Chứng minh rằng MA < MB
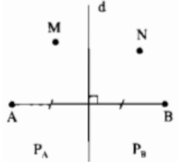
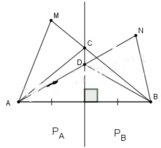
Nối MA, MB. Gọi C là giao điểm của MB với đường thẳng d, nối CA.
Ta có: MB = MC + CB
mà CA = CB (tính chất đường trung trực)
Suy ra: MB = MC + CA (1)
Trong ΔMAC ta có:
MA < MC + CA (bất đẳng thức tam giác) (2)
Từ (1) và (2) suy ra: MA < MB
Đúng 0
Bình luận (0)
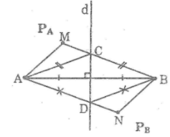
Đường trung trục d của đoạn thẳng AB chia mặt phẳng thành hai phần I và II như trên hình 10. Cho điểm M thuộc phần I và điểm N thuộc phần II.
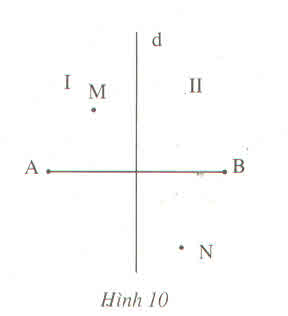
Chứng minh rằng :
a) MA < MB
b) NA > NB
a: MC+CB=MB
mà CB=CA
nên MC+CA=MB
mà MC+CA<MA
nên MA>MB
b: Gọi D là giao điểm của NA với d
C là giao điểm của CB với d
Ta có:NA=ND+DA
mà DA=DB
nen NA=ND+DB(3)
mà NB<ND+DB
nên NA>NB
Đúng 0
Bình luận (0)
Đường trung trực d của đoạn thẳng AB chia mặt phẳng thành hai phần (không kể đường thẳng d): phần chứa điểm A ký hiệu là PA, phần chứa điểm B ký hiệu là PB (hình bên). Gọi K là một điểm sao cho KA KB. Hỏi rằng K nằm ở đâu: trong PA, PB hay trên d?
Đọc tiếp
Đường trung trực d của đoạn thẳng AB chia mặt phẳng thành hai phần (không kể đường thẳng d): phần chứa điểm A ký hiệu là PA, phần chứa điểm B ký hiệu là PB (hình bên). Gọi K là một điểm sao cho KA < KB. Hỏi rằng K nằm ở đâu: trong PA, PB hay trên d?
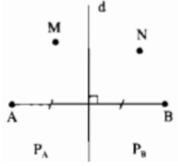
Theo phần a và b; với điểm H bất kì ta có:
+ Nếu H nằm trong phần PA thì HA < HB.
+ Nếu H nằm trong phần PB thì HB < HA.
+ Nếu H nằm trên đường thẳng d thì HA = HB (tính chất đường trung trực)
Do đó, để KA < KB thì K nằm trong phần PA.
Đúng 0
Bình luận (0)
Cho đoạn thẳng AB, đường trung trực d của AB cắt tại I . Trên cùng một nửa mặt phẳng bờ là đường thẳng AB lấy 2 điểm C và D thuộc d (D nằm giữa C và I ) , CMR :góc ADI=góc BDI
BÀI 1:Cho AB 4cm , vẽ đường thẳng d là đường trung trực của đoạn AB , lấy O thuộc d . Qua O vẽ OC 2cm sao cho OC vuông góc với d . Qua O vẽ OD 1cm sao cho OD vuông góc với d. a, Chứng tỏ rằng 3 điểm C ,O ,D thẳng hàng b, Đường thẳng d có phải là đương trung trưc của đoạn CD không ? Vì saoBÀI 2:cho tam giác ABC có ABAC.Trên nửa mặt phẳng bờ AB ko lấy điểm C,Lấy điểm M sao cho BAMb và AMAB.Trên nửa mặt phẳng Bờ AC Ko chứa A,vẽ đường thẳng d vuông góc với BC,CMR: d là đường trung trực của đoạn...
Đọc tiếp
BÀI 1:Cho AB = 4cm , vẽ đường thẳng d là đường trung trực của đoạn AB , lấy O thuộc d . Qua O vẽ OC =2cm sao cho OC vuông góc với d . Qua O vẽ OD = 1cm sao cho OD vuông góc với d. a, Chứng tỏ rằng 3 điểm C ,O ,D thẳng hàng b, Đường thẳng d có phải là đương trung trưc của đoạn CD không ? Vì sao
BÀI 2:cho tam giác ABC có AB=AC.Trên nửa mặt phẳng bờ AB ko lấy điểm C,Lấy điểm M sao cho BAM=b và AM=AB.Trên nửa mặt phẳng Bờ AC Ko chứa A,vẽ đường thẳng d vuông góc với BC,CMR: d là đường trung trực của đoạn MN
Đường trung trực d của đoạn thẳng AB chia mặt phẳng thành hai phần ( không kể đường thẳng d ): phần chứa điểm A kí hiệu là PA, phần chứa điểm B kia hiệu là PB
a, Gọi M là một điểm của PA.Cmr MAMB
b, Gọi N là một điểm của PB. Cmr NBNA
c, Gọi K là một điểm sao cho KAKB. Hỏi rằng K nằm ở đâu: trong PA,PB hay trên d
Đọc tiếp
Đường trung trực d của đoạn thẳng AB chia mặt phẳng thành hai phần ( không kể đường thẳng d ): phần chứa điểm A kí hiệu là PA, phần chứa điểm B kia hiệu là PB
a, Gọi M là một điểm của PA.Cmr MA<MB
b, Gọi N là một điểm của PB. Cmr NB<NA
c, Gọi K là một điểm sao cho KA<KB. Hỏi rằng K nằm ở đâu: trong PA,PB hay trên d