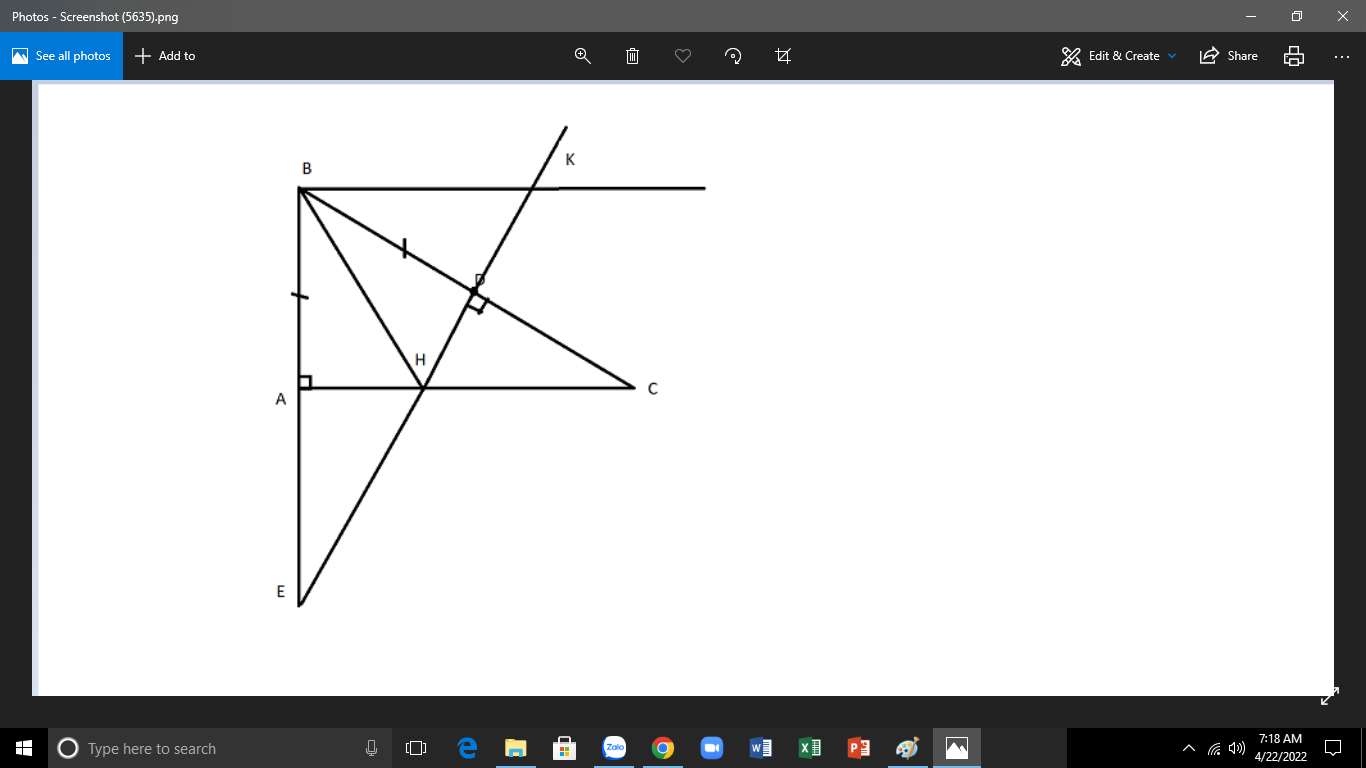
cho tam giác ABC vuông tại A và góc ABC=60 độ
a/ so sánh AB và AC
b/ Trên cạnh BC lấy D sao cho BD=AB.Qua D dựng đg thẳng vuông góc với BC cắt tia AB tai E .Chứng minh tam giác ABC=tam giác BDE
c/ gọi H là giao điểm của ED và AC. Chứng minh tia BH là tia phân giác của góc ABC
d/ qua b dựng đg vuông góc với AB cắt đg ED tại K. chứng minh HBK đều