Số chữ số tìm được là \(\dfrac{C^2_5\cdot5!}{3!}=200\)

Số số chia hết cho 3 là \(\dfrac{2\cdot5!}{3!}=40\)

\(\Rightarrow P=\dfrac{40}{200}=\dfrac{1}{5}\)

2:

\(\overline{abcd}\)

d có 1 cách chọn 

a có 3 cách chọn

b có 2 cách chọn

c có 1 cách chọn

=>Có 3*2*1*1=6 cách

1: \(\overline{abc}\)

a có 3 cách

b có 3 cách

c có 2 cách

=>Có 3*3*2=18 cách

Số chia hết cho 9 mà mỗi số xuất hiện 1 lần.

Ta có: 1+2+3+4+5+6=21

Vậy các số chia hết cho 9 sẽ có tổng các chữ số là 9 hoặc 18

Số có 2 chữ số: 36; 63; 45; 54 => 4 số

Số có 3 chữ số: 126; 621; 162; 612; 216; 261; 234; 243; 342; 324; 432; 423; 135; 153; 351; 315; 513; 531 => 18 số

Số có 4 chữ số: 3456; 3465; 3546; 3564; 3654; 3645 => 6 số x 4 cách đổi = 24 số

Số có 5 chữ số: 12456; 12465; 12564; 12546; 12645; 12654 => Số lượng: 6 x 4 x 5 = 120 số

Tổng thoả mãn: 4+18+24+120= 166(số)

Chọn C

Ta có thể chia làm bốn trường hợp sau

TH1: Số 5 có mặt một lần, số 6 có mặt một lần.( Bao gồm các khả năng sau: mỗi số có mặt một lần hoặc một số 5, một số 6 hai số 3 hoặc một số 5, một số 6 hai số 4)

Số các số được tạo thành là: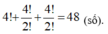 

TH2: Số 5 có mặt một lần, số 6 không có mặt.

Số các số được tạo thành là: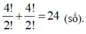 

TH3: Số 6 có mặt một lần, số 5 không có mặt.

Số các số được tạo thành là: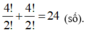 

TH4: Số 5 và số 6 không có mặt.( Số 3 và số 4 mỗi số có mặt đúng hai lần)

Số các số được tạo thành là: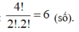 

Vậy có thể lập được 102 số thỏa mãn đề bài.

\(\overline{abcde}\)

TH1: e=0

e có 1 cách chọn

Chữ số 2 có 4 cách chọn

ba chỗ còn lại có 4*3*2=24 cách

=>Có 4*24=96 cách

TH2: e=5; a=2

a,e có 1 cach

b có 4 cách

c có 3 cách

dcó 2 cách

=>Có 4*3*2=24 cách

TH3: e=5; a<>2

e có 1 cách chọn

a có 3 cách chon

số 2 có 3 cách

hai số còn lại có 3*2=6 cách

=>Có 3*3*6=54 cách

=>CÓ 96+24+54=174 số

Gọi số cần tìm có dạng   . Vì    chia hết cho 5 suy ra e =0 hoặc 5.

TH1. Với e=0          

Nếu a=1; thì có 5 cách chọn b; 4 cách chọn c và 3 cách chọn d.

Theo quy tắc nhân có 1.5.4.3=60 số.

Tương tự nếu b=1; c=1 hoặc d=1 ta cũng có 60 số.

Trong trường hợp 1 có tất cả 60.4=240 số cần tìm.

TH2. Với e=5,

Nếu a=1 thì có 5 cách chọn b; 4 cách chọn c và 3 cách chọn c. Theo quy tắc nhân có 1.5.4.3=60 số.

Nếu b= 1 thì có 4 cách chon a( a khác 0); 4 cách chọn c và 3 cách chọn d suy ra có 1.4.4.3=48 số

Tương tự với c=1 hoặc d=1 cũng có 48 số

Trong trường hợp 2 có 60+3.48= 204.

Vậy có tất cả 204+240= 444 số cần tìm.

Chọn A.

Chọn C

Số có bốn chữ số có dạng : a b c d ¯

( a≠0,a,b,c,d∈ E={0,1,2,3,4,5})

Do  a b c d ¯  không chia hết cho 5 nên có 4 cách chọn d( là 1,2,3,4)

Chọn a ∈ E\{0,d} nên có 4 cách chọn a

Chọn b ∈ E\{a,d} nên có 4 cách chọn b

Chọn c ∈ E\{a,b,d} nên có 3 cách chọn c

Theo quy tắc nhân, có 4*4*4*3=192 số