Tìm tâm vị tự của hai đường tròn trong các trường hợp sau (h.1.62) :
Những câu hỏi liên quan
Tìm tâm vị tự của hai đường tròn trong các trường hợp sau.
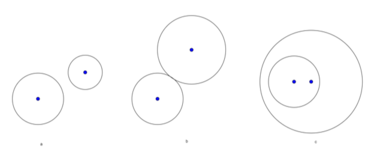
Gọi hai đường tròn lần lượt là (I; R) và (I’; R’).
Các xác định tâm vị tự của hai đường tròn:
- Trên đường tròn (I; R) lấy điểm M bất kì.
- Trên đường tròn (I’; R’) dựng đường kính AB // IM.
- MA và MB lần lượt cắt II’ tại O1 và O2 chính là hai tâm vị tự của hai đường tròn.
Đối với từng trường hợp ta xác định được các tâm vị tự O1; O2 như hình dưới.
+ Hình 1.62a:
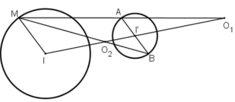
+ Hình 1.62b:
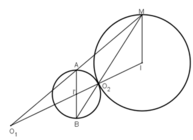
+ Hình 1.62c.
Đúng 0
Bình luận (0)
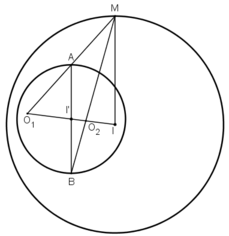
Nêu cách tìm tâm vị tự của hai đường tròn.
Gọi hai đường tròn là (I1: R1) và (I2; R2).
+ TH1: I1 ≡ I2; khi đó tâm vị tự O ≡ I1 ≡ I2; tỉ số vị tự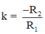 
biến đường tròn (I1; R1) thành đường tròn (I2; R2).
+ TH2: I1 ≠ I2.
Vẽ bán kính I1M bất kì.
Dựng đường kính AB của (I2; R2) sao cho AB // I1M.
MA; MB lần lượt cắt I1I2 tại O1 và O2.
Khi đó O1 và O2 chính là hai tâm vị tự của hai đường tròn.
Đúng 0
Bình luận (0)
Trong mặt phẳng với hệ tọa độ
Ox
y
cho đường tròn
C
:
x
2
+
y
2
−
2
x
−
4
y
+
4
0
và đường tròn
C
:
x
2
+
y
2
+
6
x...
Đọc tiếp
Trong mặt phẳng với hệ tọa độ Ox y cho đường tròn C : x 2 + y 2 − 2 x − 4 y + 4 = 0 và đường tròn C ' : x 2 + y 2 + 6 x + 4 y + 4 = 0. Tìm tâm vị tự của hai đường tròn?
A. I 0 ; 1 v à J 3 ; 4
B. I − 1 ; − 2 v à J 3 ; 2
C. I 1 ; 2 v à J − 3 ; − 2
D. I 1 ; 0 v à J 4 ; 3
Đáp án A
Đường tròn C có tâm K 1 ; 2 , bán kính R = 1 + 4 − 4 = 1 .
Đường tròn C ' có tâm K ' − 3 ; − 2 , bán kính R ' = 9 + 4 − 4 = 3.
Giả sử V 1 ; k C = C '
khi đó k = R ' R ⇒ k = 3 ⇔ k = ± 3
Với k = 3 ⇒ I K ' → = 3 I K → ⇒ − 3 − x 1 = 3 1 − x 1 − 2 − y 1 = 3 2 − y 1 ⇒ I 3 ; 4
Với k = − 3 ⇒ I K ' → = − 3 I K → ⇒ − 3 − x 1 = − 3 1 − x 1 − 2 − y 1 = − 3 2 − y 1 ⇒ I 0 ; 1
Đúng 0
Bình luận (0)
Trong mặt phẳng với hệ tọa độ Oxy cho đường tròn (C):
x
2
+
y
2
-
2
x
-
4
y
+
4
0
và đường tròn (C):
x
2
+
y
2
+
6
X
+
4
y
+
4
0...
Đọc tiếp
Trong mặt phẳng với hệ tọa độ Oxy cho đường tròn (C): x 2 + y 2 - 2 x - 4 y + 4 = 0 và đường tròn (C'): x 2 + y 2 + 6 X + 4 y + 4 = 0 Tìm tâm vị tự của hai đường tròn?
A. I(0;1) và J(3;4)
B. I(-1;-2) và J(3;2)
C. I(1;2) và J(-3;-2)
D. I(1;0) và J(4;3)
Nêu cách tìm tâm vị tự của hai đường tròn ?
a. Hai đường tròn tiếp xúc ngoài với nhau.
b. Hai đường tròn tiếp xúc trong với nhau
c. Một đường tròn chứa đường tròn kia
b. Hai đường tròn tiếp xúc trong với nhau
c. Một đường tròn chứa đường tròn kia
 a.a. Hai đường tròn (I;R)(I;R) và (I′;R′)(I′;R′) tiếp xúc ngoài với nhau, ta xét : *Trường hợp 1:1: Nếu R=R′R=R′ thì k=±1k=±1 Khi đó, tâm vị tự OO thỏa mãn : OI′−→−=kOI−→⇒kOI′→=kOI→⇒k chỉ có thể bằng −1−1 ⇒O⇒O (tâm vị tự trong) là trung điểm của II′II′ (chính là tiếp điểm của hai đường tròn)  *Trường hợp 2:2: Nếu R≠R′R≠R′ thì ta có thể xác định các phép vị tự sau : - Lấy A′B′A′B′ là một đường kính của đường tròn I′;R′I′;R′ và IAIA là một bán kính của (I;R)(I;R) sao cho hai véctơ IA−→IA→ và I′A′−→−I′A′→ cùng hướng - Đường thẳng II′II′ cẳt AA′,AB′AA′,AB′ lần lượt tại O1O1 (tâm vị tự ngoài) và O2O2 (tâm vị tự trong và O2O2 trùng với tiếp điểm)  b.b. Hai đường tròn (I;R),(I′;R′)(I;R),(I′;R′) tiếp xúc trong với nhau (R≠R′)(R≠R′) ta có thể xác định các phép vị tự sau : - Lấy A′B′A′B′ là một đường kính của đường tròn (I′;R′)(I′;R′) và IAIA là một bán kính của (I;R)(I;R) sao cho hai véctơ IA−→,I′A′−→−IA→,I′A′→ cùng hướng. - Đường thẳng II′II′ cắt AA′,AB′AA′,AB′ lần lượt tại O1O1 (tâm vị tự ngoài) và O2O2 (tâm vị tự trong)  c.c. Đường tròn (I;R)(I;R) nằm trong đường tròn (I′;R′)(I′;R′) ta xét : *Trường hợp 1: Nếu I≡I′I≡I′ thì khi đó tâm vị tự OO trùng với điểm II Vậy ta có hai phép vị tự : - Phép vị tự V1(I;k1)V1(I;k1) với k1=R′Rk1=R′R (biến điểm MM thành điểm M′1M1′) - Phép vị tự V2(I;k2)V2(I;k2) với k2=−R′Rk2=−R′R (biến điểm MM thành điểm M′2M2′) *Trường hợp 2:2: Nếu II không trùng với I′I′ thì ta có thể xác định các phép vị tự sau : - Lấy A′B′A′B′ là một đường kính của đường tròn (I′;R′)(I′;R′) và IAIA là một bán kính của (I;R)(I;R) sao cho hai véctơ IA−→,I′A′−→−IA→,I′A′→ cùng hướng - Đường thẳng II′II′ cắt AA′,AB′AA′,AB′ lần lượt tại O1O1 (tâm vị tự ngoài) và O2O2 (tâm vị tự trong) |
Đúng 0
Bình luận (0)
a. Hai đường tròn tiếp xúc ngoài với nhau.
b. Hai đường tròn tiếp xúc trong với nhau
c. Một đường tròn chứa đường tròn kia
b. Hai đường tròn tiếp xúc trong với nhau
c. Một đường tròn chứa đường tròn kia
|
a.a. Hai đường tròn (I;R)(I;R) và (I′;R′)(I′;R′) tiếp xúc ngoài với nhau, ta xét : *Trường hợp 1:1: Nếu R=R′R=R′ thì k=±1k=±1 Khi đó, tâm vị tự OO thỏa mãn : OI′−→−=kOI−→⇒kOI′→=kOI→⇒k chỉ có thể bằng −1−1 ⇒O⇒O (tâm vị tự trong) là trung điểm của II′II′ (chính là tiếp điểm của hai đường tròn) *Trường hợp 2:2: Nếu R≠R′R≠R′ thì ta có thể xác định các phép vị tự sau : - Lấy A′B′A′B′ là một đường kính của đường tròn và là một bán kính của sao cho hai véctơ IA−→IA→ và I′A′−→−I′A′→ cùng hướng - Đường thẳng II′II′ cẳt AA′,AB′AA′,AB′ lần lượt tại O1O1 (tâm vị tự ngoài) và O2O2 (tâm vị tự trong và O2O2 trùng với tiếp điểm) b.b. Hai đường tròn (I;R),(I′;R′)(I;R),(I′;R′) tiếp xúc trong với nhau (R≠R′)(R≠R′) ta có thể xác định các phép vị tự sau : - Lấy A′B′A′B′ là một đường kính của đường tròn (I′;R′)(I′;R′) và IAIA là một bán kính của (I;R)(I;R) sao cho hai véctơ IA−→,I′A′−→−IA→,I′A′→ cùng hướng. - Đường thẳng II′II′ cắt AA′,AB′AA′,AB′ lần lượt tại O1O1 (tâm vị tự ngoài) và O2O2 (tâm vị tự trong) c.c. Đường tròn (I;R)(I;R) nằm trong đường tròn (I′;R′)(I′;R′) ta xét : *Trường hợp 1: Nếu I≡I′I≡I′ thì khi đó tâm vị tự OO trùng với điểm II Vậy ta có hai phép vị tự : - Phép vị tự V1(I;k1)V1(I;k1) với k1=R′Rk1=R′R (biến điểm MM thành điểm M′1M1′) - Phép vị tự V2(I;k2)V2(I;k2) với k2=−R′Rk2=−R′R (biến điểm MM thành điểm M′2M2′) *Trường hợp 2:2: Nếu II không trùng với I′I′ thì ta có thể xác định các phép vị tự sau : - Lấy A′B′A′B′ là một đường kính của đường tròn (I′;R′)(I′;R′) và IAIA là một bán kính của (I;R)(I;R) sao cho hai véctơ IA−→,I′A′−→−IA→,I′A′→ cùng hướng - Đường thẳng II′II′ cắt AA′,AB′AA′,AB′ lần lượt tại O1O1 (tâm vị tự ngoài) và O2O2 (tâm vị tự trong) |
Đúng 0
Bình luận (0)
Cho nửa đường tròn tâm O đường kính AB gọi Ax By là các tia vuông góc với AB Qua M thuộc nửa đường tròn kẻ tiếp tuyến với nửa đường tròn đó cắt Ax By theo thứ tự tại C và D Chứng minh rằng
a, Kẻ MH vuông góc với AB tại H MH ra của ADN tại I Chứng minh I là trung điểm của MH
b, Tìm vị trí của M trên nửa đường tròn tâm O để chu vi ABCD đạt min
C, tìm vị trí của M trên nửa đường tròn tâm O để diện tích ABCD Đạt Min
Đọc tiếp
Cho nửa đường tròn tâm O đường kính AB gọi Ax By là các tia vuông góc với AB Qua M thuộc nửa đường tròn kẻ tiếp tuyến với nửa đường tròn đó cắt Ax By theo thứ tự tại C và D Chứng minh rằng
a, Kẻ MH vuông góc với AB tại H MH ra của ADN tại I Chứng minh I là trung điểm của MH
b, Tìm vị trí của M trên nửa đường tròn tâm O để chu vi ABCD đạt min
C, tìm vị trí của M trên nửa đường tròn tâm O để diện tích ABCD Đạt Min
Số phát biểuđúng:1. Qua phép vị tự có tỉ số
k
≠
0
, đường thẳng đi qua tâm vị tự sẽ biến thành chính nó2. Qua phép vị tự có tỉ số
k
≠
0
, đường tròn có tâm là tâm vị tự sẽ biến thành chính nó.3. Qua phép vị tự có tỉ số
k
≠
1
, không có đường tròn nào biến thành chính nó.4. Qua phép vị tự V(O;1), đường tròn tâm O sẽ biến thành chính nó.5. Phép vị tự tỉ số k biến đường thẳng thành đường thẳng song so...
Đọc tiếp
Số phát biểuđúng:
1. Qua phép vị tự có tỉ số k ≠ 0 , đường thẳng đi qua tâm vị tự sẽ biến thành chính nó
2. Qua phép vị tự có tỉ số k ≠ 0 , đường tròn có tâm là tâm vị tự sẽ biến thành chính nó.
3. Qua phép vị tự có tỉ số k ≠ 1 , không có đường tròn nào biến thành chính nó.
4. Qua phép vị tự V(O;1), đường tròn tâm O sẽ biến thành chính nó.
5. Phép vị tự tỉ số k biến đường thẳng thành đường thẳng song song hoặc trùng với đường thẳng đó
6. Phép vị tự tỉ số k biến đoạn thẳng thành đoạn thẳng mà độ dài được nhân lên với hệ số k
7. Trong phép vị tự tâm O, tỉ số k, nếu k < 0 thì điểm M và ảnh của nó ở về hai phía đối với tâm O.
8. Mọi phép dời hình đều là phép đồng dạng với tỉ số k = 1
9. Phép hợp thành của một phép vị tự tỉ số k và một phép đối xứng tâm là phép đồng dạng tỉ số
10. Hai đường tròn bất kì luôn có phép vị tự biến đường này thành đường kia
11. Khi k = 1 , phép vị tự là phép đồng nhất
12. Phép vị tự biến tứ giác thành tứ giác bằng nó
13. Khi k = 1, phép đồng dạng là phép dời hình
14. Phép đối xứng tâm là phép đồng dạng tỉ số k = 1
A.9
B.10
C.11
D.12
Đáp án C
Những phát biểuđúng: 1; 4; 5; 6; 7; 8; 9; 10; 11; 13; 14
2. Qua phép vị tự có tỉ số , đường tròn có tâm là tâm vị tự sẽ biến thành 1 đường tròn đồng tâm với đường tròn ban đầu và có bán kính = k. bán kính đường tròn ban đầu.
3. Qua phép vị tự có tỉ số đường tròn biến thành chính nó.
12. Phép vị tự với tỉ số k = biến tứ giác thành tứ giác bằng nó
Đúng 0
Bình luận (0)
Trong mặt phẳng Oxy cho đường tròn (C) có phương trình:
x
-
1
2
+
y
-
2
2
4
. Hỏi phép vị tự tâm O tỉ số k -2 biến (C) thành đường tròn nào trong các đường tròn có phương trình sau? A....
Đọc tiếp
Trong mặt phẳng Oxy cho đường tròn (C) có phương trình: x - 1 2 + y - 2 2 = 4 . Hỏi phép vị tự tâm O tỉ số k = -2 biến (C) thành đường tròn nào trong các đường tròn có phương trình sau?
A. x - 2 2 + y - 4 2 = 4
B. x + 2 2 + y + 4 2 = 4
C. x - 2 2 + y - 4 2 = 16
D. x + 2 2 + y + 4 2 = 16
Trong mặt phẳng Oxy cho đường tròn
x
-
1
2
+
y
-
1
2
4
Phép vị tự tâm O (với O là gốc tọa độ) tỉ số k 2 biến (C) thành đường tròn nào trong các đường tròn có phương trình sau?
Đọc tiếp
Trong mặt phẳng Oxy cho đường tròn x - 1 2 + y - 1 2 = 4 Phép vị tự tâm O (với O là gốc tọa độ) tỉ số k = 2 biến (C) thành đường tròn nào trong các đường tròn có phương trình sau?
