a: ĐKXĐ: x>=3

Sửa đề: \(\sqrt{4x-12}-\sqrt{9x-27}+\sqrt{\dfrac{25x-75}{4}}-3=0\)

=>\(2\sqrt{x-3}-3\sqrt{x-3}+\dfrac{5}{2}\sqrt{x-3}-3=0\)

=>\(\dfrac{3}{2}\sqrt{x-3}=3\)

=>\(\sqrt{x-3}=2\)

=>x-3=4

=>x=7(nhận)

b: ĐKXĐ: x>=0

\(\dfrac{\sqrt{x}-2}{\sqrt{x}+1}< =-\dfrac{3}{4}\)

=>\(\dfrac{\sqrt{x}-2}{\sqrt{x}+1}+\dfrac{3}{4}< =0\)

=>\(\dfrac{4\sqrt{x}-8+3\sqrt{x}+3}{4\left(\sqrt{x}+1\right)}< =0\)

=>\(7\sqrt{x}-5< =0\)

=>\(\sqrt{x}< =\dfrac{5}{7}\)

=>0<=x<=25/49

c: ĐKXĐ: x>=5

\(\sqrt{9x-45}-14\sqrt{\dfrac{x-5}{49}}+\dfrac{1}{4}\sqrt{4x-20}=3\)

=>\(3\sqrt{x-5}-14\cdot\dfrac{\sqrt{x-5}}{7}+\dfrac{1}{4}\cdot2\cdot\sqrt{x-5}=3\)

=>\(\dfrac{3}{2}\sqrt{x-5}=3\)

=>\(\sqrt{x-5}=2\)

=>x-5=4

=>x=9(nhận)

\(\dfrac{x-2}{x+1}-\dfrac{3}{x+2}>0.\left(x\ne-1;-2\right).\\ \Leftrightarrow\dfrac{x^2-4-3x-3}{\left(x+1\right)\left(x+2\right)}>0.\\ \Leftrightarrow\dfrac{x^2-3x-7}{\left(x+1\right)\left(x+2\right)}>0.\)    

Đặt \(f\left(x\right)=\dfrac{x^2-3x-7}{\left(x+1\right)\left(x+2\right)}>0.\)

Ta có: \(x^2-3x-7=0.\Rightarrow\left[{}\begin{matrix}x=\dfrac{3+\sqrt{37}}{2}.\\x=\dfrac{3-\sqrt{37}}{2}.\end{matrix}\right.\)

          \(x+1=0.\Leftrightarrow x=-1.\\ x+2=0.\Leftrightarrow x=-2.\)

Bảng xét dấu:

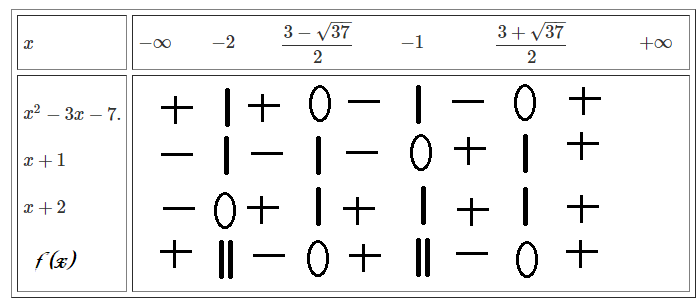
\(\Rightarrow f\left(x\right)>0\Leftrightarrow x\in\left(-\infty-2\right)\cup\left(\dfrac{3-\sqrt{37}}{2};-1\right)\cup\left(\dfrac{3+\sqrt{37}}{2};+\infty\right).\)

\(\sqrt{x^2-3x+2}\ge3.\\ \Leftrightarrow x^2-3x+2\ge9.\\ \Leftrightarrow x^2-3x-7\ge0.\)

\(\Rightarrow\left[{}\begin{matrix}x=\dfrac{3-\sqrt{37}}{2}.\\x=\dfrac{3+\sqrt{37}}{2}.\end{matrix}\right.\)

Đặt \(f\left(x\right)=x^2-3x-7.\)

\(f\left(x\right)=x^2-3x-7.\)

\(\Rightarrow f\left(x\right)\ge0\Leftrightarrow x\in(-\infty;\dfrac{3-\sqrt{37}}{2}]\cup[\dfrac{3+\sqrt{37}}{2};+\infty).\)

\(\Rightarrow\sqrt{x^2-3x+2}\ge3\Leftrightarrow x\in(-\infty;\dfrac{3-\sqrt{37}}{2}]\cup[\dfrac{3+\sqrt{37}}{2};+\infty).\)

a) \(\dfrac{2-x}{3}-x-2\le\dfrac{x-17}{2}\) \(\Leftrightarrow\) \(6\left(\dfrac{2-x}{3}-x-2\right)\le6\left(\dfrac{x-17}{2}\right)\) \(\Leftrightarrow\) 4-2x-6x-12\(\le\)3x-51 \(\Leftrightarrow\) -2x-6x-3x\(\le\)-51-4+12 \(\Leftrightarrow\) -11x\(\le\)-43 \(\Rightarrow\) x\(\ge\)43/11.

b) \(\dfrac{2x+1}{3}-\dfrac{x-4}{4}\le\dfrac{3x+1}{6}-\dfrac{x-4}{12}\) \(\Leftrightarrow\) \(12\left(\dfrac{2x+1}{3}+\dfrac{4-x}{4}\right)\le12\left(\dfrac{3x+1}{6}+\dfrac{4-x}{12}\right)\) \(\Leftrightarrow\) 8x+4+12-3x\(\le\)6x+2+4-x \(\Leftrightarrow\) 8x-3x-6x+x\(\le\)2+4-4-12 \(\Leftrightarrow\) 0x\(\le\)-10 (vô lí).

a) \(\dfrac{2-x}{3}-x-2\le\dfrac{x-17}{2}\)

\(\Leftrightarrow2\left(2-x\right)-6\left(x+2\right)\le3\left(x-17\right)\)

\(\Leftrightarrow4-2x-6x-12\le3x-51\)

\(\Leftrightarrow-11x\le-43\)

\(\Leftrightarrow x\ge\dfrac{43}{11}\)

Vậy S = {\(x\) | \(x\ge\dfrac{43}{11}\) }

b) \(\dfrac{2x+1}{3}-\dfrac{x-4}{4}\le\dfrac{3x+1}{6}-\dfrac{x-4}{12}\)

\(\Leftrightarrow4\left(2x+1\right)-3\left(x-4\right)\le2\left(3x+1\right)-\left(x-4\right)\)

\(\Leftrightarrow8x+4-3x+12\le6x+2-x+4\)

\(\Leftrightarrow0x\le-10\) (vô lý)

Vậy \(S=\varnothing\)

1) \(\sqrt[]{3x+7}-5< 0\)

\(\Leftrightarrow\sqrt[]{3x+7}< 5\)

\(\Leftrightarrow3x+7\ge0\cap3x+7< 25\)

\(\Leftrightarrow x\ge-\dfrac{7}{3}\cap x< 6\)

\(\Leftrightarrow-\dfrac{7}{3}\le x< 6\)

\(\dfrac{15x-2}{4}-\dfrac{x^2+1}{3}>\dfrac{x\left(1-2x\right)}{6}+\dfrac{x-3}{2}\\ \Leftrightarrow3\left(15x-2\right)-4\left(x^2+1\right)>2x\left(1-2x\right)+6\left(x-3\right)\\ \Leftrightarrow45x-6-4x^2-4>2x-4x^2+6x-18\\ \Leftrightarrow45x-6x-2x>6+4-18\\ \Leftrightarrow37x>-8\\ \Leftrightarrow x>-\dfrac{8}{37}\)

\(\dfrac{3\left(15x-2\right)}{12}-\dfrac{4\left(x^2+1\right)}{12}>\dfrac{2x\left(1-2x\right)}{12}+\dfrac{6\left(x-3\right)}{12}\)

\(45x-6-\left(4x^2+4\right)>2x-4x^2+6x-18\)

\(45x-4x^2+4x^2-2x-6x>6+4-18\)

\(37x>-8\)

\(x>\dfrac{-8}{37}\)

ĐKXĐ: \(\left\{{}\begin{matrix}-1\le x\le3\\x\ne1\end{matrix}\right.\)

\(\dfrac{\sqrt{x+1}\left(\sqrt{x+1}+\sqrt{3-x}\right)}{2\left(x-1\right)}>x-\dfrac{1}{2}\)

\(\Leftrightarrow\dfrac{x+1+\sqrt{-x^2+2x+3}}{x-1}>2x-1\)

- TH1: Với \(x>1\) BPT tương đương:

\(x+1+\sqrt{-x^2+2x+3}>\left(2x-1\right)\left(x-1\right)\)

\(\Leftrightarrow\sqrt{-x^2+2x+3}>2x^2-4x\)

Đặt \(\sqrt{-x^2+2x+3}=t\ge0\Rightarrow2x^2-4x=-2t^2+6\)

BPt trở thành: \(t>-2t^2+6\Leftrightarrow2t^2+t-6>0\)

\(\Rightarrow t>\dfrac{3}{2}\Rightarrow-x^2+2x+3>\dfrac{9}{4}\Rightarrow1< x< \dfrac{2+\sqrt{7}}{2}\)

TH2: với \(x< 1\) BPT tương đương:

\(x+1+\sqrt{-x^2+2x+3}< \left(2x-1\right)\left(x-1\right)\)

\(\Leftrightarrow\sqrt{-x^2+2x+3}< 2x^2-4x\)

Tương tự như trên, đặt  \(t=\sqrt{-x^2+2x+3}\ge0\) ta được \(0\le t< \dfrac{3}{2}\)

\(\Rightarrow-x^2+2x+3< \dfrac{9}{4}\) \(\Rightarrow-1\le x< \dfrac{2-\sqrt{7}}{2}\)

Vậy nghiệm của BPT là: \(\left[{}\begin{matrix}-1\le x< \dfrac{2-\sqrt{7}}{2}\\1< x< \dfrac{2+\sqrt{7}}{2}\end{matrix}\right.\)

a) Ta có: \(2\left(3x+1\right)-4\left(5-2x\right)>2\left(4x-3\right)-6\)

\(\Leftrightarrow6x+2-20+8x>8x-6-6\)

\(\Leftrightarrow14x-18-8x+12>0\)

\(\Leftrightarrow6x-6>0\)

\(\Leftrightarrow6x>6\)

hay x>1

Vậy: S={x|x>1}

b) Ta có: \(9x^2-3\left(10x-1\right)< \left(3x-5\right)^2-21\)

\(\Leftrightarrow9x^2-30x+3< 9x^2-30x+25-21\)

\(\Leftrightarrow9x^2-30x+3-9x^2+30x-4< 0\)

\(\Leftrightarrow-1< 0\)(luôn đúng)

Vậy: S={x|\(x\in R\)}