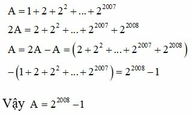A = 1 + 2 + 2 2 + . . . + 2 2007

2 A = 2 + 2 2 + . . . + 2 2007 + 2 2008

A = 2A - A =  ( 2 + 2 2 + . . . + 2 2007 + 2 2008 ) - ( 1 + 2 + 2 2 + . . . + 2 2007 ) =  2 2008 - 1

Vậy  A = 2 2008 - 1

Ta có: A =  1   +   2   +   2 2   +   . . .   +   2 2009   +   2 2010

= 1 + 2 ( 1 + 2 +  2 2 ) + ... + 2 2008  ( 1 + 2 +  2 2  )

= 1 + 2 ( 1 + 2 + 4 ) + ... + 22008 ( 1 + 2 + 4 )

= 1 + 2 . 7 + ... +  2 2008  . 7 = 1 + 7 ( 2 + ... +  2 2008  )

Mà 7 ( 2 + ... +  2 2008 ) ⋮ 7. Do đó: A chia cho 7 dư 1.

Ta có: A = 1 + 2 + 2 2  + 2 3 + ... + 2 2008  + 2 2009  + 2 2010

= 1 + 2 ( 1 + 2 + 22 ) + ... +  2 2008  ( 1 + 2 + 22 )

= 1 + 2 ( 1 + 2 + 4 ) + ... +  2 2008 ( 1 + 2 + 4 )

= 1 + 2 . 7 + ... + 2 2008 . 7 = 1 + 7 ( 2 + ... +  2 2008  )

Mà 7 ( 2 + ... +  2 2008 ) ⋮ 7. Do đó: A chia cho 7 dư 1.

1.

Đặt \(1995^{1995}=a=a_1+a_2+a_3+...+a_n\)

Gọi \(S=a_1^3+a_2^3+...+a_n^3=a_1^3+a_2^3+...+a_n^3-a+a\)

\(S=\left(a_1^3-a_1\right)+\left(a_2^3-a_2\right)+...+\left(a_n^3-a_n\right)+a\)

Vì mỗi dấu ngoặc đều chia hết cho 6 do là tích 3 số tự nhiên liên tiếp

\(\Rightarrow S\) chia 6 dư a

Mà \(1995\equiv3\left(mod6\right)\Rightarrow1995^{1995}\equiv3\left(mod6\right)\)

Vậy S chia 6 dư 3

2.

\(2^{100}=\left(2^{10}\right)^{10}=1024^{10}=\left(B\left(25\right)-1\right)^{10}=B\left(25\right)+1\)

Vì 2¹⁰⁰ chẵn nên 3 chữ số tận cùng của nó chẵn nên có thể là 126; 376; 626; 876

Lại có 2¹⁰⁰ chia hết cho 8 => ba chữ số tận cùng chi hết cho 8

=> Ba CTSC là 376

3.

\(22^{22}+55^{55}=\left(BS7+1\right)^{22}+\left(BS7-1\right)^{55}=BS7+1+BS7-1=BS7⋮7\)

\(3^{1993}=3\cdot\left(3^3\right)^{664}=3\cdot\left(BS7-1\right)^{664}=3\left(BS7+1\right)=BS7+3\) nên chia 7 dư 3

\(1992^{1993}+1994^{1995}=\left(BS7-3\right)^{1993}+\left(BS7-1\right)^{1995}=BS7-3^{1993}+BS7-1=BS7-\left(BS7+3\right)+BS7-1=BS7-4\) chia 7 dư 3

\(3^{2^{1930}}=3^{2860}=3\cdot\left(3^3\right)^{953}=3\cdot\left(BS7-1\right)^{953}=3\left(BS7-1\right)=BS7-3\) chia 7 dư 4

4.

\(2^{1994}=2^2\cdot\left(2^3\right)^{664}=4\left(BS7+1\right)^{664}=4\left(BS7+1\right)=BS7+4\) chia 7 dư 4

\(3^{1998}+5^{1998}=\left(3^3\right)^{666}+\left(5^2\right)^{999}=\left(BS7-1\right)^{666}+\left(BS7-1\right)^{999}=BS7+1+BS7-1=BS7⋮7\)

\(A=1^3+2^3+3^3+...+99^3=\left(1+2+...+99\right)^2=B^2⋮B\)

CM bằng quy nạp (có trên mạng)

a: \(A=1+2+2^2+...+2^{41}\)

=>\(2A=2+2^2+2^3+...+2^{42}\)

=>\(2A-A=2^{42}-1\)

=>\(A=2^{42}-1\)

b: \(A=\left(1+2\right)+2^2\left(1+2\right)+...+2^{40}\left(1+2\right)\)

\(=3\left(1+2^2+...+2^{40}\right)⋮3\)

\(A=\left(1+2+2^2\right)+2^3\left(1+2+2^2\right)+...+2^{39}\left(1+2+2^2\right)\)

\(=7\left(1+2^3+...+2^{39}\right)⋮7\)

b.Gọi số cần tìm là a.

Ta có: a : 3 dư 1 \(\Rightarrow\) a + 2 \(⋮\) 3

          a : 5 dư 3 \(\Rightarrow\) a + 2 \(⋮\) 5            và a là nhỏ nhất

          a : 7 dư 5 \(\Rightarrow\) a + 2 \(⋮\) 7

\(\Rightarrow\) a + 2 \(\in\) BCNN( 3, 5, 7 ).

\(\Rightarrow\) BCNN( 3, 5, 7 ) = 3.5.7 = 105.

\(\Rightarrow\) a + 2 = 105 

\(\Rightarrow\) a = 103

Nguyễn Khánh Linh

bn có thể tham khảo bài làm tương tự tại : 

Câu hỏi của nguyễn văn thành - Toán lớp 6 - Học toán với OnlineMath

(bấm vào dòng chữ màu xanh)

chúc các bn hok tốt !

Ta có : a chia 6 dư 2 => a - 2 chia hết cho 6 => a - 2 + 12 chia hết cho 6 => a + 10 chia hết cho 6

a chia 7 dư 4 => a - 4 chia hết cho 7 => a - 4 + 14 chia hết cho 7 => a + 10 chia hết cho 7

=> a + 10 chia hết cho 6 và 7

=. a + 10 thuộc BC ( 6 ; 7 )

Mà BCNN ( 6 ; 7 ) = 42

=> a + 10 thuộc B ( 42 ) = { 0 ; 42 ; ... }

=> a + 10 chia 42 dư 42

=> a chia 42 dư 32

Vậy số a chia cho 42 dư 32

a,  A = 1 + 5 3 + 5 5 + 5 7 + . . . + 5 99

B = 5 4 + 5 6 + 5 8 + . . . + 5 100 =  5 . ( 5 3 + 5 5 + 5 7 + . . . + 5 99 ) = 5(A – 1)

A + B – 1 =  5 3 + 5 4 + . . . + 5 100

5(A + B – 1) =  5 4 + 5 5 + . . . + 5 100 + 5 101

4(A + B – 1) = 5(A + B – 1) – (A + B – 1) =  5 101 - 5 3

=> A + B – 1 =  5 101 - 5 3 4

=> A + 5(A – 1) –1 =  5 101 - 5 3 4 => 6A – 6 =  5 101 - 5 3 4

=> A – 1 =  5 101 - 5 3 24

=> A =  5 101 - 5 3 + 24 24

b,  A = 1 - 2 + 2 2 - . . . - 2 2007

A = 1 + 2 2 + . . . + 2 2006 - 2 + 2 3 + . . . + 2 2007

A = ( 1 + 2 2 + . . . + 2 2006 ) - 2 . 1 + 2 2 + . . . + 2 2006

A = - 1 + 2 2 + . . . + 2 2006

Đặt  B = - 2 + 2 3 + . . . + 2 2007 =  - 2 . 1 + 2 2 + . . . + 2 2006 = 2A

A + B =  - 1 + 2 + 2 2 + . . . + 2 2006 + 2 2007

2(A+B) =  - 2 + 2 2 + . . . + 2 2006 + 2 2007 + 2 2008

A+B = 2(A+B)–(A+B) =  - 2 2008 - 1

=> A+2A =  - 2 2008 - 1

=> 3A =  - 2 2008 - 1

=> A =  - ( 2 2008 - 1 ) 3

c,  A = 7 + 7 3 + 7 5 + 7 7 + . . . + 7 1999

Đặt B =  7 2 + 7 4 + 7 6 + . . . + 7 1999 + 7 2000 =  7 ( 7 + 7 3 + 7 5 + 7 7 + . . . + 7 1999 ) = 7A

A+B =  7 + 7 2 + 7 3 + . . . + 7 1999 + 7 2000

7(A+B) =  7 2 + 7 3 + . . . + 7 1999 + 7 2000 + 7 2001

7(A+B) – (A+B) =  ( 7 2 + 7 3 + . . . + 7 1999 + 7 2000 + 7 2001 )  –  ( 7 + 7 2 + 7 3 + . . . + 7 1999 + 7 2000 )

6(A+B) =  7 2001 - 7

A+B =  7 2001 - 7 6

=> A + 7A =  7 2001 - 7 6 => 8A =  7 2001 - 7 6 => A =  7 2001 - 7 48