Gọi chân đường cao hạ từ A của tam giác ABC là H, K là giao của phân giác ngoài góc B và AH.

Đặt \(IH=x\left(x>0\right)\)

Theo hệ thức lượng: \(IB^2=IH.IK\Rightarrow IK=\frac{IB^2}{IH}=\frac{9}{x},KH=IK-IH=\frac{9}{x}-x\)

Theo định lí đường phân giác, ta có: \(\frac{IH}{IA}=\frac{KH}{KA}\)

Hay \(\frac{x}{2\sqrt{5}}=\frac{\frac{9}{x}-x}{\frac{9}{x}+2\sqrt{5}}\Leftrightarrow9+2\sqrt{5}x=\frac{18\sqrt{5}}{x}-2\sqrt{5}x\)

\(\Leftrightarrow4\sqrt{5}x^2+9x-18\sqrt{5}=0\Leftrightarrow\orbr{\begin{cases}x=\frac{3\sqrt{5}}{4}\\x=-\frac{6\sqrt{5}}{5}\left(l\right)\end{cases}}\)

Vậy \(AB=\sqrt{HA^2+HB^2}=\sqrt{\left(IH+IA\right)^2+IB^2-IH^2}\)

\(=\sqrt{\left(\frac{3\sqrt{5}}{4}+2\sqrt{5}\right)^2+3^2-\left(\frac{3\sqrt{5}}{4}\right)^2}=2\sqrt{11}.\)

Kẻ AH vuông góc với AB tại A( AH thuộc BI). Kẻ AK vuông góc với BI. Tự chứng minh tam giác AIH cân tại A => AH=AI = 2 căn 5. => IK= KH= x( x>0) Xét tam giác ABH vuông tại A=> AH2= HK x BH <=> AH2= x(2x+3). Mà AH= 2 căn 5 => x(2x+3)= 20=>x=2.5 Có AB2= BH.BK= (3+x)(3+2x)=44 => AB= 2 căn 11

Tự vẽ hình nha

giải 

Kẻ AH vuông góc với AB tại A ( AH thuộc BI ) kẻ AK vuông góc với BI

Tự chứng minh tam giác AIH cân tại A => AH = AI = 2 căn 5

                                                              => IK = KH = x ( x > 0 )

Xét tam giác ABH vuông tại A => AH2  = HK x BH

                                                 => AH2 = x ( 2x + 3 ) mà AH = 2 căn 5

=> x ( 2x + 3 ) = 20 => x = 2.5

Có AB2 = BH x BK = ( 3 + x )( 3 + 2x )=44 => AB = 2 căn 11

Hok tốt ^^

a) Áp dụng định lí Pytago vào ΔABC vuông tại A, ta được:

\(BC^2=AB^2+AC^2\)

\(\Leftrightarrow BC^2=6^2+8^2=100\)

hay BC=10(cm)

Xét ΔABC có BD là đường phân giác ứng với cạnh AC(gt)

nên \(\dfrac{AD}{AB}=\dfrac{CD}{BC}\)(Tính chất đường phân giác của tam giác)

hay \(\dfrac{AD}{6}=\dfrac{CD}{10}\)

mà AD+CD=AC(D nằm giữa A và C)

nên Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:

\(\dfrac{AD}{6}=\dfrac{CD}{10}=\dfrac{AD+CD}{6+10}=\dfrac{AC}{16}=\dfrac{8}{16}=\dfrac{1}{2}\)

Do đó: \(\dfrac{AD}{6}=\dfrac{1}{2}\)

hay AD=3(cm)

Vậy: AD=3cm

cho hình vuông MNPQ có cạnh dài 12cm. E là trung điểm của MN, H là trung điểm NP      a) tính diện tích tam giác MEQ b) tính diện tích hình thang HPQM c) so sánh s tam giác MHE và s hình vuông MNPQ GIÚP EM VỚI

đúng rồi

G là trọng tâm của \(\Delta ABC\) nên G thuộc đường trung tuyến AM (1)

Trong tam giác cân, đường trung phân giác của góc ở đỉnh đồng thời là đường trung tuyến nên I cũng thuộc đường trung tuyến AM. (2)

Từ (1) và (2) suy ra A, G, I thẳng hàng.

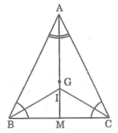
ΔABC cân tại A

⇒ phân giác AI đồng thời là trung tuyến

⇒ AI đi qua trọng tâm G của ΔABC

Vậy A, I, G thẳng hàng.

ve hinh di