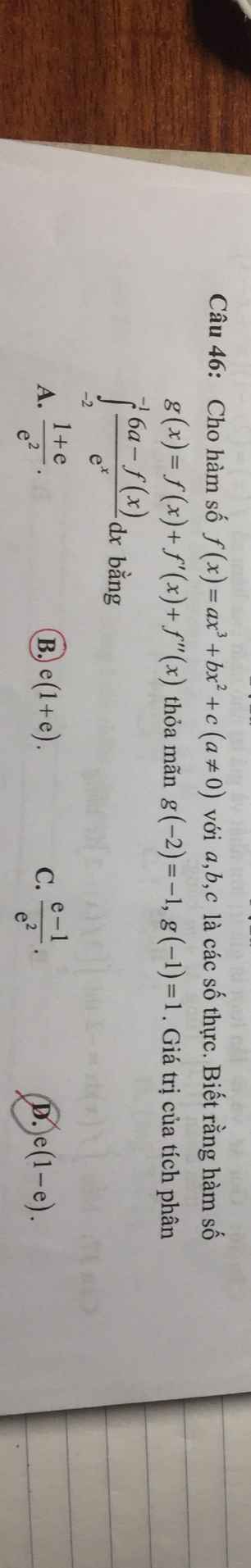ta có x^6 lớn hơn hoặc bằng 0 =>x^y lớn hơn hoặc bằng 0. Mà y là số lẻ => y lớn hơn hoặc bằng 0.

Mặt khác: x^y=x^6=> x=6 ( ko thỏa mãn y lẻ)

Vậy có 0 số nguyên x thỏa mãn

Đáp án cần chọn là: D

ta có  x 6 = 7 y ⇒ x . y = 6.7 = 42

mà 

42 = 42.1 = 1.42 = 2.21 = 21.2 = 3.14 = 14.3 = 6.7 = 7.6 = − 42 . ( − 1 ) = ( − 1 ) . ( − 42 ) = ( − 2 ) . ( − 21 ) = ( − 21 ) . ( − 2 ) = ( − 3 ) . ( − 14 ) = ( − 14 ) . ( − 3 ) = ( − 6 ) . ( − 7 ) = ( − 7 ) . ( − 6 )

và x,y∈Z,x < y < 0 nên (x;y)∈{(−42;−1),(−21;−2),(−14;−3),(−7;−6)}

a, Giả sử số cần tìm là \(\overline{abcde}\) \(\left(a\ne b\ne c\ne d\ne e,a\ne0\right)\)

- Chọn a có 9 cách.

- Chọn b, c, d, e có \(A^4_9\) cách

⇒ Có: \(9.A^4_9=27216\) (số)

b, Gọi số cần tìm là \(\overline{abcde}\) \(\left(a\ne b\ne c\ne d\ne e,a\ne0,e\in\left\{1,3,5,7,9\right\}\right)\)

- Chọn e có 5 cách.

- Chọn a có 8 cách.

- Chọn b, c, d có \(A^3_8\) cách.

⇒ Có \(5.8.A^3_8=13440\) (số)

a.Gọi số cần tìm là abcde

a có 9 cách chọn

b có 9 cách chọn

c có 8 cách chọn

d có 7 cách chọn

e có 6 cách chọn

Vậy có 9.9.8.7.6 = 27216 số thỏa mãn đề bài

b.Nếu e=0 thì a có 9 cách chọn; b có 8 cách chọn; c có 7 cách chọn; d có 6 cách chọn

Nếu e={2;4;6} thì a có 8 cách chọn; b có 8 cách chọn; c có 7 cách chọn; d có 6 cách chọn

Vậy có 9.8.7.6+8.8.7.6.3=11088 số thỏa mãn đề bài

Đặt x=y=k

x^2+py^2/xy=k^2+py^2/k^2=k^2(p+1)/k^2=p+1

\(I=\int\limits^{-1}_{-2}\dfrac{6a}{e^x}dx-\int\limits^{-1}_{-2}\dfrac{f\left(x\right)}{e^x}dx=J-I_1\)

Xét \(I_1\) , đặt \(\left\{{}\begin{matrix}u=f\left(x\right)\\dv=e^{-x}dx\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}du=f'\left(x\right)dx\\v=-e^{-x}\end{matrix}\right.\)

\(\Rightarrow I_1=-f\left(x\right).e^{-x}|^{-1}_{-2}+\int\limits^{-1}_{-2}\dfrac{f'\left(x\right)}{e^x}dx=-f\left(-1\right).e+f\left(-2\right).e^2+I_2\)

Xét \(I_2\) , đặt \(\left\{{}\begin{matrix}u=f'\left(x\right)\\dv=e^{-x}dx\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}du=f''\left(x\right)dx\\v=-e^{-x}\end{matrix}\right.\)

\(\Rightarrow I_2=-f'\left(x\right).e^{-x}|^{-1}_{-2}+\int\limits^{-1}_{-2}\dfrac{f''\left(x\right)}{e^x}dx=-f'\left(-1\right).e+f'\left(-2\right).e^2+I_3\)

Xét \(I_3\) , đặt \(\left\{{}\begin{matrix}u=f''\left(x\right)\\dv=e^{-x}dx\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}du=f'''\left(x\right)dx=6a.dx\\v=-e^{-x}\end{matrix}\right.\)

\(\Rightarrow I_3=-f''\left(x\right).e^{-x}|^{-1}_{-2}+\int\limits^{-1}_{-2}\dfrac{6a}{e^x}dx=-f''\left(-1\right).e+f''\left(-2\right).e^2+J\)

Do đó:

\(I=J+f\left(-1\right).e-f\left(-2\right).e^2+f'\left(-1\right).e-f'\left(-2\right).e^2+f''\left(-1\right).e-f''\left(-2\right).e^2-J\)

\(=e\left[f\left(-1\right)+f'\left(-1\right)+f''\left(-1\right)\right]-e^2\left[f\left(-2\right)+f'\left(-2\right)+f''\left(-2\right)\right]\)

\(=e.g\left(-1\right)-e^2.g\left(-2\right)=e+e^2=e\left(e+1\right)\)

ta có :

x,y nguyên thì \(\left|xy\right|\text{ và }\left|x-y\right|\text{ là các số nguyên không âm nên }\orbr{\begin{cases}xy=0\\x-y=0\end{cases}}\)

với \(xy=0\Rightarrow\orbr{\begin{cases}x=0\Rightarrow y=\pm1\\y=0\Rightarrow x=\pm1\end{cases}}\)

với \(x-y=0\Rightarrow x=y=\pm1\)

vậy có 6 cập x,y nguyên thỏa mãn là (0,1) ,(0,-1), (1,0), (-1,0) ,(1,1), (-1,-1)