Cho đường thẳng d: x - 2y + 1 = 0. Viết phương trình đường thẳng d dưới dạng chính tắc và tham số.

Những câu hỏi liên quan
Viết phương trình tham số và phương trình chính tắc của đường thẳng (d): x + y - 20 = 0
\(\left(d\right):x+y-20=0.\\ \Rightarrow\overrightarrow{n_d}=\left(1;1\right).\\ \Rightarrow\overrightarrow{u_d}=\left(1;-1\right).\)
\(Cho\) \(x=1.\Rightarrow y=19.\Rightarrow A\left(1;19\right)\in\left(d\right).\)
Ta có \(\left(d\right):\) đi qua \(A\left(1;19\right);\overrightarrow{u_d=}\left(1;-1\right)\) là vecto chỉ phương.
\(\Rightarrow\) Phương trình tham số:
\(\left\{{}\begin{matrix}y=1+t.\\y=19-t.\end{matrix}\right.\)
\(\Rightarrow\) Phương trình chính tắc:
\(\dfrac{x-1}{1}=\dfrac{y-19}{-1}.\\ \Leftrightarrow x-1=-y+19.\)
Đúng 1
Bình luận (1)
(d):x+y−20=0.⇒→nd=(1;1).⇒→ud=(1;−1).(d):x+y−20=0.⇒nd→=(1;1).⇒ud→=(1;−1).
ChoCho x=1.⇒y=19.⇒A(1;19)∈(d).x=1.⇒y=19.⇒A(1;19)∈(d).
Ta có (d):(d): đi qua A(1;19);−−−→ud=(1;−1)A(1;19);ud=→(1;−1) là vecto chỉ phương.
⇒⇒ Phương trình tham số:
{y=1+t.y=19−t.{y=1+t.y=19−t.
⇒⇒ Phương trình chính tắc:
HT
Đúng 0
Bình luận (0)
Trong không gian Oxyz, cho mặt phẳng (P) có phương trình x+2y+z-40 và đường thẳng d:
x
+
1
2
y
1
z
+
2
3
. Viết phương trình chính tắc của đường thẳng Δ nằm trong mặt phẳng (P), đồng thời cắt và vuông góc với đường thẳng d A.
x...
Đọc tiếp
Trong không gian Oxyz, cho mặt phẳng (P) có phương trình x+2y+z-4=0 và đường thẳng d: x + 1 2 = y 1 = z + 2 3 . Viết phương trình chính tắc của đường thẳng Δ nằm trong mặt phẳng (P), đồng thời cắt và vuông góc với đường thẳng d
A. x + 5 1 = y - 1 1 = z - 3 1
B. x - 5 1 = y + 1 1 = z + 3 1
C. x - 1 5 = y - 1 - 1 = z - 1 - 3
D. x + 1 5 = y + 1 - 1 = z + 1 - 3
Trong không gian Oxyz, cho mặt phẳng (P) có phương trình
x
+
2
y
+
z
-
4
0
và đường thẳng
d
:
x
+
1
2
y
1
z
+
3
2
. Viết phương trình chính tắc của đường thẳng∆nằm...
Đọc tiếp
Trong không gian Oxyz, cho mặt phẳng (P) có phương trình x + 2 y + z - 4 = 0 và đường thẳng d : x + 1 2 = y 1 = z + 3 2 . Viết phương trình chính tắc của đường thẳng∆nằm trong mặt phẳng (P), đồng thời cắt và vuông góc với đường thẳng d.
![]()
![]()
![]()
![]()
Đáp án C.
Gọi I là giao điểm của d và (P). Tọa độ I là nghiệm của hệ:
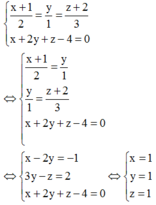
Ta có một vecto chỉ phương của ∆ như sau:
![]()
Vậy phương trình:
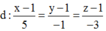
Chú ý: Do ∆ cắt d và ∆ nằm trong (P) nên ∆ phải đi qua I. Do đó ta có thể chọn được đáp là C mà không cần tìm VTCP của∆.
Đúng 0
Bình luận (0)
Cho
M
1
;
0
;
3
, đường thẳng
d
:
x
y
z
và
P
:
x
-
2
y
+
4
0
. Viết phương trình tham số của đường thẳng
∆
qua M,
∆...
Đọc tiếp
Cho M 1 ; 0 ; 3 , đường thẳng d : x = y = z và P : x - 2 y + 4 = 0 . Viết phương trình tham số của đường thẳng ∆ qua M, ∆ ∥ P và ∆ cắt (d).
![]()
![]()
![]()
![]()
Trong không gian với hệ tọa độ Oxyz, cho đường thẳng d có phương trình tham số
x
2
+
t
y
-
3
t
z
-
1
+...
Đọc tiếp
Trong không gian với hệ tọa độ Oxyz, cho đường thẳng d có phương trình tham số x = 2 + t y = - 3 t z = - 1 + 5 t . Phương trình chính tắc của đường thẳng d là?
A. x - 2 = y = z + 1
B. x - 2 1 = y - 3 = z + 1 5
C. x + 2 - 1 = y 3 = z - 1 - 5
D. x + 2 1 = y - 3 = z - 1 5
Chọn B.
Đường thẳng d đi qua điểm A(2;0;-1) và có vectơ chỉ phương ![]()
Vậy phương trình chính tắc của d là x - 2 1 = y - 3 = z + 1 5
Đúng 0
Bình luận (0)
Trong mặt phẳng toạ độ Oxy, cho hai điểm A(3;1),B(4;-2) và đường thẳng d: -x+2y+1=0. a) Viết phương trình tham số của Δ đi qua A song song với đường thẳng d b) Viết phương trình tổng quát của Δ đi qua B và vuông góc với đường thẳng d c) Viết phương trình đường tròn có bán kính AB
a: (Δ)//d nên Δ: -x+2y+c=0
=>VTPT là (-1;2)
=>VTCP là (2;1)
PTTS là:
x=3+2t và y=1+t
b: (d): -x+2y+1=0
=>Δ: 2x+y+c=0
Thay x=4 và y=-2 vào Δ, ta được:
c+8-2=0
=>c=-6
Đúng 0
Bình luận (0)
Trong không gian với hệ tọa độ Oxyz, cho đường thẳng d có phương trình tham số
x
2
+
t
y
3
-
t
z
-
1
+...
Đọc tiếp
Trong không gian với hệ tọa độ Oxyz, cho đường thẳng d có phương trình tham số x = 2 + t y = 3 - t z = - 1 + 5 t . Phương trình chính tắc của đường thẳng d là?
A. x - 2 = y = z + 1
B. x - 2 1 = y - 3 = z + 1 5
C. x + 2 - 1 = y 3 = z - 1 - 5
D. x + 2 1 = y - 3 = z - 1 5
Chọn B.
Đường thẳng d đi qua điểm A(2;0;-1) và có vectơ chỉ phương ![]()
Vậy phương trình chính tắc của d là x - 2 1 = y - 3 = z + 1 5
Đúng 0
Bình luận (0)
Trong mặt phẳng tọa độ cho hai điểm A(3;0), B(0;2) và đường thẳng d: x + y 0.a) Lập phương trình tham số của đường thẳng Δ đi qua A và song song với db) Lập phương trình đường tròn đi qua A,B và có tâm thuộc đường thẳng dc) Lập phương trình chính tắc của elip đi qua điểm B và có tâm sai
e
5
3
Đọc tiếp
Trong mặt phẳng tọa độ cho hai điểm A(3;0), B(0;2) và đường thẳng d: x + y = 0.
a) Lập phương trình tham số của đường thẳng Δ đi qua A và song song với d
b) Lập phương trình đường tròn đi qua A,B và có tâm thuộc đường thẳng d
c) Lập phương trình chính tắc của elip đi qua điểm B và có tâm sai e = 5 3
Đường thẳng Δ song song với d ⇒ Δ: x + y + c = 0, (c ≠ 0)
Vì Δ đi qua A ⇒ 3 + 0 + c = 0 ⇒ c = -3(tm)
Vậy đường thẳng Δ có dạng: x+y-3=0
Vì đường tròn có tâm I thuộc d nên I(a;-a)
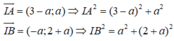
Vì đường tròn đi qua A, B nên I A 2 = I B 2 ⇒ (3 - a ) 2 + a 2 = a 2 + (2 + a ) 2 ⇔ (3 - a ) 2 = (2 + a ) 2
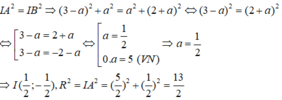
Vậy phương trình đường tròn có dạng:
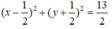
Ta có:
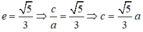
Giả sử elip (E) có dạng:
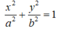
Vì (E) đi qua B nên:
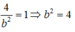
Mà
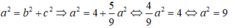
Vậy phương trình chính tắc của elip (E) là:
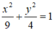
Đúng 0
Bình luận (0)
Trong không gian Oxyz, lập phương trình chính tắc của đường thẳng d đi qua điểm M(0;1;-1), nằm trong mặt phẳng (P): x + 2y + z - 1 0 và vuông góc với đường thẳng A.
d
:
x
9
y
-
1
-
2
z
+
3...
Đọc tiếp
Trong không gian Oxyz, lập phương trình chính tắc của đường thẳng d đi qua điểm M(0;1;-1), nằm trong mặt phẳng (P): x + 2y + z - 1 = 0 và vuông góc với đường thẳng 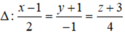
A. d : x 9 = y - 1 - 2 = z + 3 4
B. d : x 9 = y - 1 2 = z + 1 5
C. d : x 9 = y + 1 - 2 = z - 1 - 5
D. d : x 9 = y + 1 2 = z - 1 - 5














