Câu 5:Hàm số bằng 0 khi
Giả sử
khác
,khi đó ta có

Những câu hỏi liên quan
HÀM số y=ax^2+bx+c bằng 0 khi x=1.Giả sử b khác 0 khi đó ta có a+c/b bằng
hàm số y=ax^2+bx+c bằng 0 khi x=1. giả sử b khác 0, khi đó ta có a+c/b=
hàm số y=ax^2+bx+c bằng 0 khi x=1. giả sử b khác 0, khi đó ta cóa+c/b=
x=1 => \(x=1\Rightarrow y=ax^2+bx+c=a.1+b.1+c=a+b+c=0\)
Giả sử b khác 0 => a + c = - b để thỏa mãn cho a+b+c=0 => \(\frac{a+c}{b}=\frac{-b}{b}=-1\)
Đúng 0
Bình luận (0)
hàm số y=ax^2+bx+c bằng 0 khi x=1. giả sử b khác 0, khi đó ta có a+c/b= (đang cần gấp kết quả, ai xong trc tick ngay)
Hàm số \(y=ax^2+bx+c\)
bắng 0 khi x=1.
Giả sử b khác 0, khi đó ta có \(\frac{a+c}{b}=........\)
Từ \(x=1\Rightarrow a+b+c=0\)
\(\Rightarrow a+c=-b\)
\(\Rightarrow\frac{a+c}{-b}=1\Rightarrow\frac{a+c}{b}=-1\)
Đúng 0
Bình luận (0)
\(y=ax^2+bx+c=a1^2+b1+c=a+b+\)\(c=0\)
b khác 0 suy ra a và c trái dấu
a và c trái dấu suy ra a+c =0
khi đó ta có \(\frac{a+c}{b}=0\)
Đúng 0
Bình luận (0)
Hàm số y=ax^2 +bx+c bằng 0 khi x=1Giả sử bkhác 0,khi đó ta có a+c/b = ?
Giả sử hàm số
y
a
x
4
+
b
x
2
+
c
có đồ thị như hình vẽ. Khi đó:
Đọc tiếp
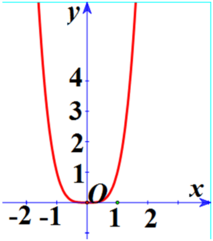
Giả sử hàm số y = a x 4 + b x 2 + c có đồ thị như hình vẽ. Khi đó:
![]()
![]()
![]()
![]()
Chọn B.
Đồ thị hướng lên nên a > 0 . Có 1 cực trị nên a b ≥ 0 suy ra b ≥ 0 . Qua (0; 0) nên c = 0 . Do đó chọn câu B.
Đúng 0
Bình luận (0)
Giả sử hàm số
y
a
x
4
+
b
x
2
+
c
có đồ thị như hình vẽ. Khi đó
Đọc tiếp
Giả sử hàm số y = a x 4 + b x 2 + c có đồ thị như hình vẽ. Khi đó

![]()
![]()
![]()
![]()
Chọn D.
Đồ thị hướng xuống và có 3 cực trị nên a < 0 , b > 0 suy ra câu A ( c không có điều kiện)
Đúng 0
Bình luận (0)
Giả sử tiếp tuyến của đồ thị hàm số y = 2 x 3 - 6 x 2 + 18 x + 1 song song với đường thẳng d:12x - y = 0 có dạng là y = ax + b . Khi đó tổng a+b là
A. 15
B. -27
C. 12
D. 11
Giả sử đồ thị (C) của hàm số
f
x
a
x
3
+
b
x
2
+
c
x
+
d
có hai điểm cực trị là
M
(
-
1
;
7
)
và
N
(
5
;
-
7
)
. Gọi
x
1
;
...
Đọc tiếp
Giả sử đồ thị (C) của hàm số f x = a x 3 + b x 2 + c x + d có hai điểm cực trị là M ( - 1 ; 7 ) và N ( 5 ; - 7 ) . Gọi x 1 ; x 2 ; x 3 là hoành độ giao điểm của (C) với trục hoành. Khi đó x 1 + x 2 + x 3 bằng
A. 6
B. 4
C. 3
D. 2













