Các câu hỏi tương tự
Số giao điểm của đồ thị hàm số y = (x − 3)( x 2 + x + 4) với trục hoành là:
A. 2; B. 3;
C. 0; D. 1.
Số giao điểm của đồ thị hàm số y = (x − 3)( x 2 + x + 4) với trục hoành là:
A. 2; B. 3;
C. 0; D. 1
Cho hàm số y f(x)
a
x
+
b
c
x
+
d
( a,b,c,d
∈
ℝ
,
-
d
c
≠
0) đồ thị hàm số y f’(x) như hình vẽ. Biết đồ thị hàm số y f(x) cắt...
Đọc tiếp
Cho hàm số y = f(x) = a x + b c x + d ( a,b,c,d ∈ ℝ , - d c ≠ 0) đồ thị hàm số y= f’(x) như hình vẽ.

Biết đồ thị hàm số y= f(x) cắt trục tung tại điểm có tung độ bằng 3. Tìm phương trình tiếp tuyến của (C) tại giao điểm của (C) với trục hoành ?
A. y = x - 3 x + 1
B. y = x + 3 x - 1
C. y = x + 3 x + 1
D. y = x - 3 x - 1
Hoành độ các điểm cực tiểu của hàm số y = x 4 + 3 x 2 + 2 là:
A. x = −1; B. x = 5;
C. x = 0; D. x = 1, x = 2.
Hoành độ các điểm cực tiểu của hàm số y = x 4 + 3 x 2 + 2 là:
A. x = −1; B. x = 5;
C. x = 0; D. x = 1, x = 2.
Cho hàm số
y
x
+
2
2
x
+
3
có đồ thị (C). Giả sử, đường thẳng d: ykx+m là tiếp tuyến của (C), biết rằng d cắt trục hoành, trục tung lần lượt tại hai điểm phân biệt A, B và tam giác
∆
O
A
B
cân tại gốc tọa độ O. Tổng k+m có giá trị bằng: A. 1. B. 3. C. -1. D. -3.
Đọc tiếp
Cho hàm số y = x + 2 2 x + 3 có đồ thị (C). Giả sử, đường thẳng d: y=kx+m là tiếp tuyến của (C), biết rằng d cắt trục hoành, trục tung lần lượt tại hai điểm phân biệt A, B và tam giác ∆ O A B cân tại gốc tọa độ O. Tổng k+m có giá trị bằng:
A. 1.
B. 3.
C. -1.
D. -3.
Cho hai hàm số
f
(
x
)
x
4
-
m
-
1
x
2
+
2
và
g
(
x
)
2
x
4
-
4
x...
Đọc tiếp
Cho hai hàm số f ( x ) = x 4 - m - 1 x 2 + 2 và g ( x ) = 2 x 4 - 4 x 2 + 3 m . Giả sử đồ thị hàm số f(x) có ba điểm cực trị là A, B, C và đồ thị hàm số g(x) có ba điểm cực trị là M, N, P. Có bao nhiêu giá trị của tham số m để hai tam giác ABC và MNP đồng dạng với nhau?
A. 1.
B. 0.
C. 2.
D. 3.
Cho hai hàm số
f
(
x
)
a
x
3
+
b
x
2
+
c
x
-
1
2
và
g
(
x
)
d
x
2
+
e
x
+
1
(
a
,
b
,
c
,
d...
Đọc tiếp
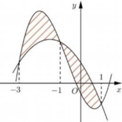
Cho hai hàm số f ( x ) = a x 3 + b x 2 + c x - 1 2 và g ( x ) = d x 2 + e x + 1 ( a , b , c , d , e ∈ ℝ ) . Biết rằng đồ thị của hàm số y = f(x) và y = g(x) cắt nhau tại ba điểm có hoành độ lần lượt là –3; –1;1 (tham khảo hình vẽ). Hình phẳng giới hạn bởi hai đồ thị đã cho có diện tích bằng
A. 9 2
B. 8
C. 4
D. 5
Đồ thị của hàm số f(x)
x
3
+
3
x
2
+
b
x
+
c
tiếp xúc với trục hoành tại gốc tọa độ và cắt đường thẳng x 1 tại điểm có tung độ bằng 3 khi A. a b 0; c 2 B. a c 0; b 2 C. a 2; b c 0 D. a 2; b 1; c 0
Đọc tiếp
Đồ thị của hàm số f(x) = x 3 + 3 x 2 + b x + c tiếp xúc với trục hoành tại gốc tọa độ và cắt đường thẳng x = 1 tại điểm có tung độ bằng 3 khi
A. a = b = 0; c = 2
B. a = c = 0; b = 2
C. a = 2; b = c = 0
D. a = 2; b = 1; c = 0




