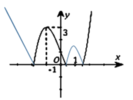
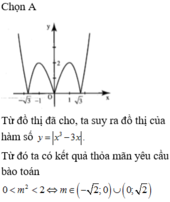
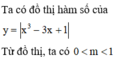Tìm nghiệm của phương trình x3 - 3x + 1

Những câu hỏi liên quan
tìm nghiệm nguyên của phương trình : x3 - x2y + 3x -2y - 5 = 0
Lời giải:
PT $\Leftrightarrow x^3+3x-5=x^2y+2y=y(x^2+2)$
$\Rightarrow y=\frac{x^3+3x-5}{x^2+2}$
Để $y$ nguyên thì $x^3+3x-5\vdots x^2+2$
$\Leftrightarrow x(x^2+2)+x-5\vdots x^2+2$
$\Leftrightarrow x-5\vdots x^2+2(1)$
$\Rightarrow x^2-5x\vdots x^2+2$
$\Leftrightarrow x^2+2-(5x+2)\vdots x^2+2$
$\Leftrightarrow 5x+2\vdots x^2+2(2)$
Từ $(1);(2)\Rightarrow 5(x-5)-(5x+2)\vdots x^2+2$
$\Leftrightarrow 27\vdots x^2+2$. Do $x^2+2\geq 2$ nên:
$\Rightarrow x^2+2\in\left\{3;9;27\right\}$
$\Rightarrow x^2\in\left\{1;7;25\right\}$
Do $x$ nguyên nên $x\in\left\{\pm 1; \pm 5\right\}$
Thay vào $y$ ta tìm được:
$x=-1\Rightarrow y=-3$
$x=5\Rightarrow y=5$
Đúng 2
Bình luận (0)
Tìm tất cả giá trị của m để phương trình
x
3
-
3
x
-
m
+
1
0
có ba nghiệm phân biệt A. m 1 B. C. –1
≤
m
≤
3 D. –1m3
Đọc tiếp
Tìm tất cả giá trị của m để phương trình x 3 - 3 x - m + 1 = 0 có ba nghiệm phân biệt
A. m = 1
B. 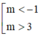
C. –1 ≤ m ≤ 3
D. –1<m<3
Đáp án D
Phương pháp giải:
Cô lập tham số m, đưa về khảo sát hàm số để biện luận số nghiệm của phương trình
Lời giải:
Xét hàm số ![]() có
có ![]()
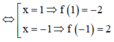
Để phương trình F(x) = m – 1 có 3 nghiệm phân biệt
![]()
Đúng 0
Bình luận (0)
Cho hàm số
y
x
3
-
3
x
+
1
có đồ thị là hình vẽ bên. Tìm m để phương trình |
x
3
-
3
x
+
1
| có 6 nghiệm thực phân biệt
Đọc tiếp
Cho hàm số y = x 3 - 3 x + 1 có đồ thị là hình vẽ bên. Tìm m để phương trình | x 3 - 3 x + 1 | có 6 nghiệm thực phân biệt
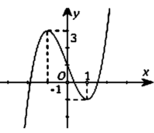
![]()
![]()
![]()
![]()
Cho hàm số
y
x
3
-
3
x
+
1
có đồ thị là hình vẽ bên. Tìm m để phương trình
x
3
-
3
x
+
1
m
có 6 nghiệm thực phân biệt A. -1 m 0 B. -1 m 3 C. 0 m 1 D. 0 m 3
Đọc tiếp
Cho hàm số y = x 3 - 3 x + 1 có đồ thị là hình vẽ bên. Tìm m để phương trình x 3 - 3 x + 1 = m có 6 nghiệm thực phân biệt
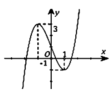
A. -1 < m < 0
B. -1 < m < 3
C. 0 < m < 1
D. 0 < m < 3
Cho đồ thị hàm số
y
-
x
3
+
3
x
+
1
là hình vẽ bên. Tìm m để phương trình
y
x
3
-
3
x
+
m
0
có 3 nghiệm phân biệt. A. -2m2 B. -2m3 C. -1m3 D. -1m2
Đọc tiếp
Cho đồ thị hàm số y = - x 3 + 3 x + 1 là hình vẽ bên. Tìm m để phương trình y = x 3 - 3 x + m = 0 có 3 nghiệm phân biệt.
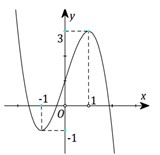
A. -2<m<2
B. -2<m<3
C. -1<m<3
D. -1<m<2
Tìm m để phương trình:
x
3
-
3
x
+
2
log
2
4
m
2
+
1
có 4 nghiệm thực phân biệt. A.
m
≥
1
B. ...
Đọc tiếp
Tìm m để phương trình: x 3 - 3 x + 2 = log 2 4 m 2 + 1 có 4 nghiệm thực phân biệt.
A. m ≥ 1
B. m ≤ 1
C. m ≤ 1 m ≠ 0
D. m < 1
Đáp án C
Vẽ đồ thị hàm số y = x 3 - 3 x + 2 = [ x 3 - 3 x + 2 x 3 - 3 x + 2 ≥ 0 - x 3 - 3 x + 2 x 3 - 3 x + 2 < 0
Gồm 2 phần (hình bên dưới)
Phần 1: là đồ thị hàm số y = x 3 - 3 x + 2
Phần 2: lấy đối xứng đồ thị hàm số y = x 3 - 3 x + 2 qua trục Ox
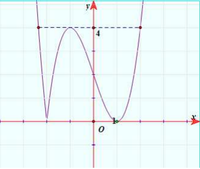
Khi đó nghiệm của phương trình x 3 - 3 x + 2 = log 2 4 m 2 + 1 là số giao điểm của (C) và đường thẳng y = log 2 4 m 2 + 1
Vật phương trình có 4 nghiệm ⇔ 0 < log 2 4 m 2 + 1 < 4 ⇔ 0 < 4 log 2 m 2 + 1 < 4
1 < m 2 + 1 < 2 ⇔ m 2 < 1 ⇔ - 1 < m < 1 m ≠ 0
Đúng 0
Bình luận (0)
Hình bên là đồ thị của hàm số
y
x
3
-
3
x
. Tìm tất cả các giá trị thực của tham số m để phương trình
x
3
-
3
x
2
m
có 4 nghiệm phân biệt A. -2 m 0 B. -2 ≤ m C. -1 ≤ m D. -1 m 0
Đọc tiếp
Hình bên là đồ thị của hàm số y = x 3 - 3 x . Tìm tất cả các giá trị thực của tham số m để phương trình x 3 - 3 x = 2 m có 4 nghiệm phân biệt
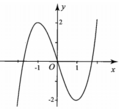
A. -2 < m < 0
B. -2 ≤ m
C. -1 ≤ m
D. -1 < m < 0
Hình bên là đồ thị của hàm số
y
x
3
-
3
x
. Tìm tất cả các giá trị thực của tham số m để phương trình
x
3
-
3
x
m
2
có 6 nghiệm phân biệt A.
m
∈
-
2...
Đọc tiếp
Hình bên là đồ thị của hàm số y = x 3 - 3 x . Tìm tất cả các giá trị thực của tham số m để phương trình x 3 - 3 x = m 2 có 6 nghiệm phân biệt
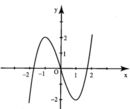
A. m ∈ - 2 ; 0 ∪ 0 ; 2
B. m ∈ 0 ; 2
C. m ∈ - 2 ; 0 ∪ 0 ; 2
D. m ∈ 0 ; 2
Hình bên là đồ thị của hàm số
y
x
3
-
3
x
Tìm tất cả các giá trị thực của tham số m để phương trình
x
3
-
3
x...
Đọc tiếp
Hình bên là đồ thị của hàm số y = x 3 - 3 x Tìm tất cả các giá trị thực của tham số m để phương trình x 3 - 3 x = m 2 có 6 nghiệm phân biệt.
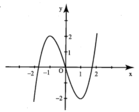
A.![]()
B. ![]()
C. ![]()
D. ![]()
Đáp án A
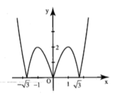
Từ đồ thị đã cho, ta suy ra đồ thị của hàm số ![]()
Từ đó ta có kết quả thỏa mãn yêu cầu bào toán ![]()
Đúng 0
Bình luận (0)
Tìm tất cả các nghiệm nguyên x, y của phương trình x3 + 2x2 + 3x + 2 = y3.
+, Nếu x = 0 => ko tồn tại y thuộc Z
+, Nếu x khác 0 => x^2 >= 1 => x^2-1 >= 0
Có : y^3 = x^3+2x^2+3x+2 > x^3 ( vì 2x^2+3x+2 > 0 )
Lại có : y^3 = (x^3+3x^3+3x+1)-(x^2-1) = (x+1)^3 - (x^2-1) < = (x+1)^3
=> x^3 < y^3 < = (x+1)^3
=> y^3 = (x+1)^3
=> x^2-1 = 0
=> x=-1 hoặc x=1
+, Với x=-1 thì y = 0
+, Với x=1 thì y = 2
Vậy .............
Tk mk nha
Đúng 1
Bình luận (0)
Ta có: \(x^3+2x^2+3x+2=y^3\) (1)
Xét \(2x^2+3x+2=2\left(x^2+\frac{3}{2}x\right)+2=2\left(x^2+\frac{3}{2}x+\frac{9}{16}\right)+2-2.\frac{9}{16}\)
\(=2\left(x+\frac{3}{4}\right)^2+\frac{7}{8}\) Vì \(\left(x+\frac{3}{4}\right)^2\ge0\Rightarrow2\left(x+\frac{3}{4}\right)^2+\frac{7}{8}\ge\frac{7}{8}>0\)
\(\Rightarrow y^3>x^3\Rightarrow y^3\ge\left(x+1\right)^3\)
\(\Rightarrow x^3+2x^2+3x+2\ge\left(x+1\right)^3\) \(\Rightarrow x^3+2x^2+3x+2\ge x^3+3x^2+3x+1\)
\(\Rightarrow x^3+3x^2+3x+1-x^3-2x^2-3x-2\le0\)
\(\Rightarrow x^2-1\le0\Rightarrow x^2\le1\) Vì \(x\in Z\Rightarrow\orbr{\begin{cases}x^2=1\\x^2=0\end{cases}}\)
+ TH1: x2 = 0 => x =0 Thay vào pt (1) ta được y3 = 2 (loại) vì y nguyên
+ TH2 : x2 = 1 => \(\orbr{\begin{cases}x=1\\x=-1\end{cases}}\)
Thay x=1 vào pt (1) ta đc: 1+2+3+2 = 8 = y3 => y = 2
Thay x= -1 vào pt (1) ta đc: -1 + 2 -3 +2 = 0 =y3 => y = 0
Vậy cặp (x;y) là (1;2) ; (-1;0).
Đúng 0
Bình luận (0)
\(Xét \(2x^2+3x+2=2\left(x+\dfrac{3}{4}\right)^2+\dfrac{7}{16}>0\forall x\in R\) => \(x^3< y^3\left(1\right)\) (1) Giả sử : \(y^3< \left(x+2\right)^3\) \(\Leftrightarrow x^3+2x^2+3x+2< x^3+6x^2+12x+8\) \(\Leftrightarrow-4x^2-9x-6< 0\) \(\Leftrightarrow4x^2+9x+6>0\) \(\Leftrightarrow4\left(x+\dfrac{9}{8}\right)^2+\dfrac{15}{64}>0\) => Giả sử đúng . => \(y^3< \left(x+2\right)^3\left(2\right)\) Từ (1)(2) => \(y^3=\left(x+1\right)^3\) \(\Leftrightarrow x^3+2x^2+3x+2=x^3+3x^2+3x+1\) \(\Leftrightarrow x^2=1\) \(\Leftrightarrow\left[{}\begin{matrix}x=1\\x=-1\end{matrix}\right.\) .) Khi \(x=1\Rightarrow y=2\). .) Khi \(x=-1\Rightarrow y=0\) Vậy nghiệm của pt ( x;y ) = {( 1;2 ) ; ( -1;0 )}\)
Đúng 0
Bình luận (0)