\(\frac{x}{-5}\)=\(\frac{y}{-6}\)

Những câu hỏi liên quan
Tìm các số nguyên x,y sao cho
a,\(\frac{x}{3}=\frac{5}{y}\)
b,\(\frac{3}{x}+\frac{y}{3}=\frac{5}{6}\)
c,\(\frac{5}{x}-\frac{y}{3}=\frac{1}{6}\)
d,\(\frac{x}{6}-\frac{2}{y}=\frac{1}{30}\)
a )x.y=3.5 => x.y =1.15=3.5
x thuộc 1 , 15 , 3 ,5
y thuộc 1,15 , 3 ,5
b )x = 18
y = 2
c ) x= 30
y =0
d phần này mk chưa ra
Đúng 0
Bình luận (0)
Cho hàm số y sin xa) Tìm giá trị y tương ứng với giá trị của x trong bảng sau:x - pi - frac{{5pi }}{6} - frac{pi }{2} - frac{pi }{6}0frac{pi }{6}frac{pi }{2}frac{{5pi }}{6}pi y sin x?????????b) Trong mặt phẳng Oxy, hãy biểu diễn các điểm left( {x;y} right) trong bảng giá trị ở câu a. Bằng cách làm tương tự, lấy nhiều điểm left( {x;sin x} right) với x in left[ { - pi ;pi } right] với nối lại ta được đồ thị hàm số y sin x trên đoạn left[ { - pi ;pi } right] (Hình 24). c) Làm tương t...
Đọc tiếp
Cho hàm số \(y = \sin x\)
a) Tìm giá trị y tương ứng với giá trị của x trong bảng sau:
x | \( - \pi \) | \( - \frac{{5\pi }}{6}\) | \( - \frac{\pi }{2}\) | \( - \frac{\pi }{6}\) | 0 | \(\frac{\pi }{6}\) | \(\frac{\pi }{2}\) | \(\frac{{5\pi }}{6}\) | \(\pi \) |
\(y = \sin x\) | ? | ? | ? | ? | ? | ? | ? | ? | ? |
b) Trong mặt phẳng Oxy, hãy biểu diễn các điểm \(\left( {x;y} \right)\) trong bảng giá trị ở câu a. Bằng cách làm tương tự, lấy nhiều điểm \(\left( {x;\sin x} \right)\) với \(x \in \left[ { - \pi ;\pi } \right]\) với nối lại ta được đồ thị hàm số \(y = \sin x\) trên đoạn \(\left[ { - \pi ;\pi } \right]\) (Hình 24).
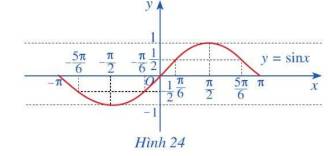
c) Làm tương tự như trên đối với các đoạn \(\left[ { - 3\pi ; - \pi } \right]\), \(\left[ {\pi ;3\pi } \right]\), ...ta có đồ thị hàm số \(y = \sin x\)trên R được biểu diễn ở Hình 25.
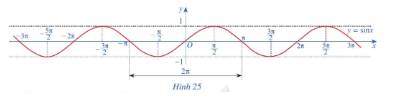
a)
x | \( - \pi \) | \( - \frac{{5\pi }}{6}\) | \( - \frac{\pi }{2}\) | \( - \frac{\pi }{6}\) | 0 | \(\frac{\pi }{6}\) | \(\frac{\pi }{2}\) | \(\frac{{5\pi }}{6}\) | \(\pi \) |
\(y = \sin x\) | 0 | \( - \frac{1}{2}\) | -1 | \( - \frac{1}{2}\) | 0 | \(\frac{1}{2}\) | 1 | \(\frac{1}{2}\) | 0 |
b) Trong mặt phẳng Oxy, hãy biểu diễn các điểm \(\left( {x;y} \right)\) trong bảng giá trị ở câu a. Bằng cách làm tương tự, lấy nhiều điểm \(\left( {x;\sin x} \right)\) với \(x \in \left[ { - \pi ;\pi } \right]\) với nối lại ta được đồ thị hàm số \(y = \sin x\) trên đoạn \(\left[ { - \pi ;\pi } \right]\)(Hình 24).
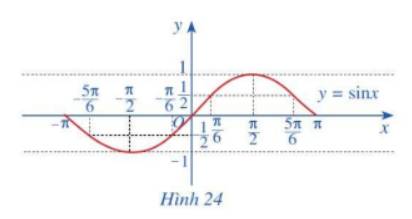
c) Làm tương tự như trên đối với các đoạn \(\left[ { - 3\pi ; - \pi } \right]\), \(\left[ {\pi ;3\pi } \right]\),...ta có đồ thị hàm số \(y = \sin x\)trên R được biểu diễn ở Hình 25.
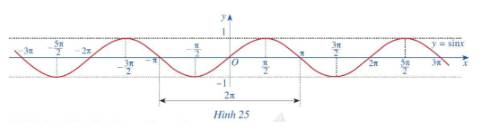
Đúng 0
Bình luận (0)
tìm x , y biết
a, \(\frac{4}{x}+\frac{y}{3}=\frac{5}{6}\)
b, \(\frac{5}{x}-\frac{y}{3}=\frac{1}{6}\)
c, \(\frac{x}{6}-\frac{2}{y}=\frac{1}{30}\)
1a)tìm x,y biết: 4+frac{x}{7+y}frac{4}{7}and:x+y22b)cho frac{x}{3}frac{y}{4}và frac{y}{5}frac{z}{6}. Tính Mfrac{2x+3y+4z}{3x+4y+5z}c) tìm x biết frac{1}{4}.frac{2}{6}.frac{3}{8}.frac{4}{10}...frac{30}{62}.frac{31}{64}2^xd)frac{4^5+4^5+4^5+4^5}{3^5+3^5+3^5}.frac{6^5+6^5+6^5+6^5+6^5+6^5}{2^5+2^5}2x2. Tính:P1+frac{1}{2}left(1+2right)+frac{1}{3}left(1+2+3right)+...+frac{1}{16}left(1+2+..+16right)
Đọc tiếp
1a)tìm x,y biết: \(4+\frac{x}{7+y}=\frac{4}{7}and:x+y=22\)
b)cho \(\frac{x}{3}=\frac{y}{4}\)và \(\frac{y}{5}=\frac{z}{6}\). Tính M=\(\frac{2x+3y+4z}{3x+4y+5z}\)
c) tìm x biết \(\frac{1}{4}.\frac{2}{6}.\frac{3}{8}.\frac{4}{10}...\frac{30}{62}.\frac{31}{64}=2^x\)
d)\(\frac{4^5+4^5+4^5+4^5}{3^5+3^5+3^5}.\frac{6^5+6^5+6^5+6^5+6^5+6^5}{2^5+2^5}=2x\)
2. Tính:P=\(1+\frac{1}{2}\left(1+2\right)+\frac{1}{3}\left(1+2+3\right)+...+\frac{1}{16}\left(1+2+..+16\right)\)
Câu b) tạm thời ko bít làm =.=
Bài 1 :
\(d)\) \(\frac{4^5+4^5+4^5+4^5}{3^5+3^5+3^5}.\frac{6^5+6^5+6^5+6^5+6^5+6^5}{2^5+2^5}=2x\)
\(\Leftrightarrow\)\(\frac{4^5.4}{3^5.3}.\frac{6^5.6}{2^5.2}=2x\)
\(\Leftrightarrow\)\(\frac{4^6}{3^6}.\frac{6^6}{2^6}=2x\)
\(\Leftrightarrow\)\(\frac{2^{12}}{3^6}.\frac{2^6.3^6}{2^6}=2x\)
\(\Leftrightarrow\)\(\frac{2^{12}}{3^6}.\frac{3^6}{1}=2x\)
\(\Leftrightarrow\)\(2^{12}=2x\)
\(\Leftrightarrow\)\(x=\frac{2^{12}}{2}\)
\(\Leftrightarrow\)\(x=2^{11}\)
\(\Leftrightarrow\)\(x=2048\)
Vậy \(x=2048\)
Chúc bạn học tốt ~
Đúng 0
Bình luận (0)
Bài 1 :
\(a)\) Ta có :
\(4+\frac{x}{7+y}=\frac{4}{7}\)
\(\Leftrightarrow\)\(\frac{x}{7+y}=\frac{4}{7}-4\)
\(\Leftrightarrow\)\(\frac{x}{7+y}=\frac{-24}{7}\)
\(\Leftrightarrow\)\(\frac{x}{-24}=\frac{7+y}{7}\)
Áp dụng tính chất dãy tỉ số bằng nhau ta có :
\(\frac{x}{-24}=\frac{7+y}{7}=\frac{x+7+y}{-24+7}=\frac{22+7}{-17}=\frac{29}{-17}=\frac{-29}{17}\)
Do đó :
\(\frac{x}{-24}=\frac{-29}{17}\)\(\Rightarrow\)\(x=\frac{-29}{17}.\left(-24\right)=\frac{696}{17}\)
\(\frac{7+y}{7}=\frac{-29}{17}\)\(\Rightarrow\)\(y=\frac{-29}{17}.7-7=\frac{-322}{17}\)
Vậy \(x=\frac{696}{17}\) và \(y=\frac{-322}{17}\)
Chúc bạn học tốt ~
Đúng 0
Bình luận (0)
2.
Ta có 1+2+...+n=n.(n+1):2
=>P=\(1+\frac{1}{2}.\frac{2.3}{2}+\frac{1}{3}.\frac{3.4}{2}+...+\)\(\frac{1}{16}.\frac{16.17}{2}\)=1+\(\frac{3}{2}+\frac{4}{2}+...+\frac{17}{2}\)=1+\(\frac{1}{2}.\left(3=4+..=17\right)\)
=1+\(\frac{1}{2}.153=1+\frac{153}{2}=\frac{155}{2}\)
Đúng 0
Bình luận (0)
Xem thêm câu trả lời
Tim x,y\(\in\) z biet :
a)\(\frac{x}{3}-\frac{2}{y}=\frac{1}{5}\) b)\(\frac{2}{x}-\frac{y}{3}=\frac{5}{6}\)
c)\(\frac{5}{x}-\frac{y}{3}=\frac{1}{6}\) d) \(\frac{x}{6}-\frac{2}{y}=\frac{1}{4}\)
Tìm x , y :
\(\frac{x+3}{y+5}=\frac{3}{5}\) va x + y = 6
\(\frac{x-7}{y-6}=\frac{7}{6}va\) x - y = -4
a) Thay x=6-y
ta có: \(\frac{6-y+3}{y+5}=\frac{3-y}{y+5}=\frac{3}{5}\)
\(\Rightarrow\left(3-y\right).5=\left(y+5\right).3\)
15 - 5y= 3y + 15
-5y-3y=15-15
-8y=0
y=0
Vậy x=6
b) Thay x= y-4
ta có: \(\frac{y-4-7}{y-6}=\frac{y-11}{y-6}=\frac{7}{6}\)
\(\Rightarrow\left(y-11\right).6=\left(y-6\right).7\)
6y-66 = 7y -42
-y=24
y=-24
Vậy x=-4+-24=-28
Đúng 0
Bình luận (0)
\(\frac{x+3}{y+5}=\frac{3}{5}\\ \Leftrightarrow5\left(x+3\right)=3\left(y+5\right)\\ \Leftrightarrow5x+15=3y+15\\ \Leftrightarrow5x=3y\\ M\text{à};x+y=6\Rightarrow x=6-y\\ \Rightarrow5\left(6-y\right)=3y\\ \Leftrightarrow30-5y=3y\\ \Rightarrow30=8y\\ \Rightarrow y=\frac{30}{8}\\ \)
\(\frac{x-7}{y-6}=\frac{7}{6}\\ \Leftrightarrow6\left(x-7\right)=7\left(y-6\right)\\ \Leftrightarrow6x-42=7y-42\\ \Leftrightarrow6x=7y\\ M\text{à}x-y=-4;\Rightarrow x=-4+y\\ \Rightarrow6\left(-4+y\right)=7y\\ \Rightarrow-24+6y=7y\\ \Rightarrow y=-24\\ \)
Từ y bạn từ tìm x nhé!!!
Đúng 0
Bình luận (0)
tìm cặp số tự nhiên sao cho:
a, \(\frac{4}{x}-\frac{y}{3}=\frac{5}{6}\)( x, y thuộc N )
b, \(\frac{5}{x}-\frac{y}{3}=\frac{1}{6}\) ( x , y thuộc Z )
c, \(\frac{x}{6}_{ }-\frac{2}{y}=\frac{1}{30}\) ( x, y thuộc Z )
Nội qui tham gia "Giúp tôi giải toán"
1. Không đưa câu hỏi linh tinh lên diễn đàn, chỉ đưa các bài mà mình không giải được hoặc các câu hỏi hay lên diễn đàn;
2. Không trả lời linh tinh, không phù hợp với nội dung câu hỏi trên diễn đàn.
3. Không "Đúng" vào các câu trả lời linh tinh nhằm gian lận điểm hỏi đáp.
Các bạn vi phạm 3 điều trên sẽ bị giáo viên của Online Math trừ hết điểm hỏi đáp, có thể bị khóa tài khoản hoặc bị cấm vĩnh viễn không đăng nhập vào trang web.
mong các bn đừng làm như vậy nah
Đúng 0
Bình luận (0)
giải hpt
a) \(\left\{{}\begin{matrix}\frac{5}{x-1}+\frac{1}{y-1}=10\\\frac{1}{x-1}-\frac{3}{y-1}=18\end{matrix}\right.\)
b)\(\left\{{}\begin{matrix}\frac{7}{\sqrt{x-7}}-\frac{4}{\sqrt{y+6}}=\frac{5}{2}\\\frac{5}{\sqrt{x-7}}+\frac{3}{\sqrt{y+6}}=\frac{13}{6}\end{matrix}\right.\)
a) Đặt \(\left\{{}\begin{matrix}\frac{1}{x-1}=a\\\frac{1}{y-1}=b\end{matrix}\right.\)
\(hpt\Leftrightarrow\left\{{}\begin{matrix}5a+b=10\\a-3b=18\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}15a+3b=30\\a-3b=18\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}a-3b=18\\16a=48\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}a=3\\b=-5\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}\frac{1}{x-1}=3\\\frac{1}{y-1}=-5\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=\frac{4}{3}\\y=\frac{4}{5}\end{matrix}\right.\)
Vậy...
b) Đặt \(\left\{{}\begin{matrix}\frac{1}{\sqrt{x-7}}=a\\\frac{1}{\sqrt{y+6}}=b\end{matrix}\right.\)
\(hpt\Leftrightarrow\left\{{}\begin{matrix}7a-4b=\frac{5}{2}\\5a+3b=\frac{13}{6}\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}31a-12b=\frac{15}{2}\\20a+12b=\frac{26}{3}\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}7a-4b=\frac{5}{2}\\51a=\frac{97}{6}\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}a=\frac{97}{306}\\b=\frac{-43}{612}\end{matrix}\right.\)( loại vì \(a,b>0\) )
Vậy hệ vô nghiệm
Is that true .-.
Đúng 0
Bình luận (0)
Cho xin solve lại câu b)
hpt \(\Leftrightarrow\left\{{}\begin{matrix}21a-12b=\frac{15}{2}\\20a+12b=\frac{26}{3}\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}5a+3b=\frac{13}{6}\\41a=\frac{97}{6}\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}a=\frac{97}{246}\\b=\frac{8}{123}\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}\frac{1}{\sqrt{x-7}}=\frac{97}{246}\\\frac{1}{\sqrt{y+6}}=\frac{8}{123}\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=\frac{126379}{9409}\\y=\frac{14745}{64}\end{matrix}\right.\)
Vậy...
Đúng 0
Bình luận (1)
\(y=\frac{6:\frac{3}{5}-1\frac{1}{6}x\frac{6}{7}}{4\frac{1}{5}x\frac{10}{11}+5\frac{2}{11}}\)=?
\(=\frac{6\times\frac{5}{3}-\frac{7}{6}\times\frac{6}{7}}{\frac{21}{5}\times\frac{10}{11}+\frac{57}{11}}=\frac{10-1}{\frac{42}{11}+\frac{57}{11}}=\frac{9}{\frac{99}{11}}\)=1
Đúng 0
Bình luận (0)
a,\(\hept{\begin{cases}\frac{1}{x-2}+\frac{1}{y-x}=1\\\frac{2}{x-2}-\frac{3}{y-1}=1\end{cases}}\) b,\(\hept{\begin{cases}\frac{7}{\sqrt{x-7}}-\frac{4}{\sqrt{y+6}}=\frac{5}{3}\\\frac{5}{\sqrt{x-y}}+\frac{3}{\sqrt{y+6}}=\frac{13}{6}\end{cases}}\)
Giải hpt này giúp em với ạ
Mình đề câu a phải như vậy nè:
\(a,\hept{\begin{cases}\frac{1}{x-2}+\frac{1}{y-1}=1\\\frac{2}{x-2}-\frac{3}{y-1}=1\end{cases}}\)\(Đkxđ:\hept{\begin{cases}x\ne2\\y\ne1\end{cases}}\)
Đặt: \(X=\frac{1}{x-2};Y=\frac{1}{y-1}\)
Ta có hệ sau:
\(\hept{\begin{cases}X+Y=1\\2X-3Y=1\end{cases}\Leftrightarrow\hept{\begin{cases}X=1-Y\\2\left(1-Y\right)-3Y=1\end{cases}}}\Leftrightarrow\hept{\begin{cases}X=1-Y\\2-5Y=1\end{cases}\Leftrightarrow\hept{\begin{cases}X=\frac{4}{5}\\Y=\frac{1}{5}\end{cases}}}\)
Với \(X=\frac{4}{5}\Rightarrow\frac{1}{x-2}=\frac{4}{5}\Leftrightarrow4\left(x-2\right)=5\Leftrightarrow x=\frac{13}{4}\)
Với \(Y=\frac{1}{5}\Rightarrow\frac{1}{y-1}=\frac{1}{5}\Leftrightarrow y-1=5\Leftrightarrow y=6\)
Vậy nghiệm của hệ pt là: \(\left(x;y\right)=\left(\frac{13}{4};6\right)\)
Câu b e nghĩ đề như vậy nè:
\(b,\hept{\begin{cases}\frac{7}{\sqrt{x-7}}-\frac{4}{\sqrt{y+6}}=\frac{5}{3}\\\frac{5}{\sqrt{x-7}}+\frac{3}{\sqrt{y+6}}=\frac{3}{6}\end{cases}}\) \(Đkxđ:\hept{\begin{cases}x>7\\x>-6\end{cases}}\)
Đặt \(\frac{1}{\sqrt{x-7}}=a\left(a>0\right);\frac{1}{\sqrt{y+6}}=b\left(b>0\right)\)
Ta có hệ pt mới: \(\hept{\begin{cases}7a-4b=\frac{5}{3}\\5a+3b=\frac{13}{6}\end{cases}}\Leftrightarrow\hept{\begin{cases}a=\frac{1}{3}\\b=\frac{1}{6}\end{cases}}\left(tmđk\right)\)
\(\Rightarrow\hept{\begin{cases}\frac{1}{\sqrt{x-7}}=\frac{1}{3}\\\frac{1}{\sqrt{y+6}}=\frac{1}{6}\end{cases}}\Leftrightarrow\hept{\begin{cases}\sqrt{x-7}=3\\\sqrt{y+6}=6\end{cases}}\Leftrightarrow\hept{\begin{cases}x-7=9\\x+6=36\end{cases}}\Leftrightarrow\hept{\begin{cases}x=16\\y=30\end{cases}\left(tmđk\right)}\)
Vậy hệ pt có nghiệm \(\left(x,y\right)=\left(16;30\right)\)






















