giải hệ pt : xa+xb=6
xa+xc=10
xb+xc=4
tìm x
a, 2^5= 4^x
b, 2. 4^2 . 8^3. 16 ^4=8^x
c,3^3:3^5=9^x
Giải:
a) \(2^5=4^x\)
\(\Rightarrow2^5=\left(2^2\right)^x\)
\(\Rightarrow2^5=2^{2x}\)
\(\Rightarrow2x=5\)
\(\Rightarrow x=\dfrac{5}{2}\)
b) \(2.4^2.8^3.16^4=8^x\)
\(\Rightarrow2.\left(2^2\right)^2.\left(2^3\right)^3.\left(2^4\right)^4=\left(2^3\right)^x\)
\(\Rightarrow2.2^4.2^9.2^{16}=2^{3x}\)
\(\Rightarrow2^{30}=2^{3x}\)
\(\Rightarrow3x=30\)
\(\Rightarrow x=30:3\)
\(\Rightarrow x=10\)
c) \(3^3:3^5=9^x\)
\(\Rightarrow3^{-2}=\left(3^2\right)^x\)
\(\Rightarrow3^{-2}=3^{2x}\)
\(\Rightarrow2x=-2\)
\(\Rightarrow x=-2:2\)
\(\Rightarrow x=-1\)
Chúc bạn học tốt!
a) Ta có: \(2^5=4^x\)
nên \(2^{2x}=2^5\)
\(\Leftrightarrow2x=5\)
hay \(x=\dfrac{5}{2}\)
b) Ta có: \(2\cdot4^2\cdot8^3\cdot16^4=8^x\)
\(\Leftrightarrow2^{3x}=2\cdot2^5\cdot2^9\cdot2^{16}=2^{31}\)
\(\Leftrightarrow3x=31\)
hay \(x=\dfrac{31}{3}\)
c) Ta có: \(3^3:3^5=9^x\)
\(\Leftrightarrow3^{-2}=3^{2x}\)
\(\Leftrightarrow2x=-2\)
hay x=-1
Viết chương trình C++ sử dụng các hàm và thủ tục xây dựng ở trên để giải bài toán:
Cho tệp dữ liệu TAMGIAC.DAT có cấu trúc như sau:
- Dòng đầu tiên chứa số N;
- N dòng tiếp theo, mỗi dòng chứa 6 số thực xA, yA, xB, yB, xC, yC là tọa độ 3 đỉnh A(xA, yA), B(xB, yB), C(xC, yC) của tam giác ABC
Hãy nhập dữ liệu từ tệpđã cho và trong số N tam giác đó, đưa ra tệp TAMGIAC.OUT gồm 3 dòng:
- Dòng đầu tiên là số lượng tam giác đều;
- Dòng thứ 2 là số lượng tam giác cân (nhưng không là đều);
- Dòng thứ 3 là số lượng tam giác vuông.
(Viet chuong trinh C++ chu khong phai Pascal a )
Viết chương trình sử dụng các hàm và thủ tục xây dựng ở trên để giải bài toán:
Cho tệp dữ liệu TAMGIAC.DAT có cấu trúc như sau:
- Dòng đầu tiên chứa số N;
- N dòng tiếp theo, mỗi dòng chứa 6 số thực xA, yA, xB, yB, xC, yC là tọa độ 3 đỉnh A(xA, yA), B(xB, yB), C(xC, yC) của tam giác ABC
Hãy nhập dữ liệu từ tệpđã cho và trong số N tam giác đó, đưa ra tệp TAMGIAC.OUT gồm 3 dòng:
- Dòng đầu tiên là số lượng tam giác đều;
- Dòng thứ 2 là số lượng tam giác cân (nhưng không là đều);
- Dòng thứ 3 là số lượng tam giác vuông.
const fi='tamgiac.dat'
fo='tamgiac.out'
var f1,f2:text;
a,b,c,d,e,f:array[1..100]of integer;
i,n,dem1,dem2,dem3:integer;
ab,bc,ac:real;
begin
assign(f1,fi); reset(f1);
assign(f2,fo); rewrite(f2);
readln(f1,n);
for i:=1 to n do
readln(f1,a[i],b[i],c[i],d[i],e[i],f[i]);
dem1:=0;
dem2:=0;
dem3:=0;
for i:=1 to n do
begin
ab:=sqrt(sqr(a[i]-c[i])+sqr(b[i]-d[i]));
ac:=sqrt(sqr(a[i]-e[i])+sqr(b[i]-f[i]));
bc:=sqrt(sqr(c[i]-e[i])+sqr(d[i]-f[i]));
if (ab>0) and (ac>0) and (bc>0) and (ab+ac>bc) and (ab+bc>ac) and
(ac+bc>ab) then
begin
if (ab=ac) or (ac=bc) then inc(dem1);
if ((ab=ac) and (ab<>bc) and (ac<>bc)) then inc(dem2);
if ((ac=bc) and (bc<>ab) and (ac<>ab)) then inc(dem2);
if ((ac=bc) and (ac<>ab) and (bc<>ab)) then inc(dem2);
if sqr(ab)=sqr(ac)+sqr(bc) then inc(dem3);
if sqr(ac)=sqr(bc)+sqr(ab) then inc(dem3);
if sqr(bc)=sqr(ab)+sqr(ac) then inc(dem3);
end;
end;
writeln(f2,dem1);
writeln(f2,dem2);
writeln(f2,dem3);
close(f1);
close(f2);
end.
Viết Chương trình diện tích tứ giác ABCD khi biết tọa độ Điểm A(xA,yA); B(xB,yB); C(xC,yC); D(xD,yD)
Cho ba điểm A, B, C nằm trên hệ trục tọa độ Đề Các, có tọa độ lần lượt là (XA, YA), (XB, YB), (XC, YC).Tìm khoảng cách lớn nhất d giữa hai điểm trong 3 điểm trên
Trong không gian Oxyz Cho A(0; 0; a), B(b; 0; 0), C(0; c; 0). Phương trình mặt phẳng (ABC) là:
A. x a + y b + z c = 1 B. x a + y c + z b = 1
C. x b + y c + z a = 1 D. x c + y b + z a = 1
Chọn C.
Phương trình mặt phẳng theo đoạn chắn (ABC) là:
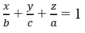
biết 2 đại lượng x và y tỉ lệ thuận và khi x =6 y=4
a) tìm hệ số tỉ lệ k của y đối với x
b) biểu diễn y theo x
c) tính giá trị của y khi x=10
Lập chương trình nhập vào tọa độ 3 đỉnh A(Xa, Ya), B(Xb, Yb), C(Xc, Yc) của 1 tam giác
a, Tính Chu vi, Diện tích
b, Kiểm tra tính chất và cho biết đây là tam giác cân, đều hay vuông.
uses crt;
var xa,ya,xb,yb,xc,yc:integer;
ab,ac,bc,cv,p,s:real;
begin
clrscr;
write('Nhap toa do diem A:'); readln(xa,ya);
write('Nhap toa do diem B:'); readln(xb,yb);
write('Nhap toa do diem C:'); readln(xc,yc);
ab:=sqrt(sqr(xa-xb)+sqr(ya-yb));
ac:=sqrt(sqr(xa-xc)+sqr(ya-yc));
bc:=sqrt(sqr(xb-xc)+sqr(yb-yc));
if (ab+bc>ac) and (ab+ac>bc) and (ac+bc>ab) then
begin
cv:=ab+bc+ac;
p:=cv/2;
s:=sqrt(p*(p-ab)*(p-ac)*(p-bc));
writeln('Chu vi la: ',cv:4:2);
writeln('Dien tich la: ',dt:4:2);
kt:=0;
if (ab=ac) and (ab<>bc) and (ac<>bc) then kt:=1;
if (ac=bc) and (ac<>ab) and (bc<>ab) then kt:=1;
if (ab=bc) and (ab<>ac) and (bc<>ac) then kt:=1;
if (ab=ac) and (ac=bc) then kt:=2;
if sqr(ab)=sqr(ac)+sqr(bc) then kt:=3;
if sqr(ac)=sqr(ab)+sqr(bc) then kt:=3;
if sqr(bc)=sqr(ab)+sqr(ac) then kt:=3;
if kt=0 then writeln('Day la tam giac thuong');
if kt=1 then writeln('Day la tam giac can');
if kt=2 then writeln('Day la tam giac deu');
if kt=3 then writeln('Day la tam giac vuong');
end
else writeln('Day khong phai la toa do 3 dinh cua mot tam giac');
readln;
end.
Cho tam giác ABC nhọn. Về phía ngoài tam giác vẽ tam giác XBC có XB = XC và goác BXC = 120 độ. Vẽ các tam giác YCA và ZAB đều ra phía ngoài tam giác ABC. CMR: XA vuông góc với YZ