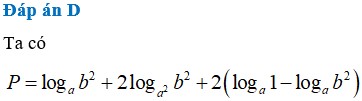1 

(3x-2)(4x+5)=0

⇔ 3x-2=0  -> x= 2/3      

 ⇔ 4x-5=0     x= 5/4

Vậy tập nghiệm S = { 2/3; 5/4}

2,    (4x+2)(\(X^2\)+3)=0

⇔ 4x+2=0         ->   x= -1/2    

     \(x^2\)+3=0         -> x= \(\sqrt{3}\); -\(\sqrt{3}\)

Vaayj tập nghiệm S= { -1/2; \(\sqrt{3}\);-\(\sqrt{3}\)}

3)

    (2x+7)(x-3)(5x-1)=0

⇔ 2x+7=0          ->   x= -7/2

     x-3   =0         ->     x =  3

    5x-1  =0         ->    x=  1/5

Vậy tập nghiệm S={ -7/2; 3; 1/5}

1) Ta có: \(\left(-5+x\right)\left(x-7\right)=0\)

\(\Leftrightarrow\left[{}\begin{matrix}-5+x=0\\x-7=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=5\\x=7\end{matrix}\right.\)

Vậy: \(x\in\left\{5;7\right\}\)

2) Ta có: \(\left(30-x\right)\left(2x-16\right)=0\)

\(\Leftrightarrow\left[{}\begin{matrix}30-x=0\\2x-16=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}-x=-30\\2x=16\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=30\\x=8\end{matrix}\right.\)

Vậy: \(x\in\left\{30;8\right\}\)

3) Ta có: \(\left(-5-x\right)\left(17+x\right)=0\)

\(\Leftrightarrow\left[{}\begin{matrix}-5-x=0\\17+x=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}-x=5\\x=0-17\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=-5\\x=-17\end{matrix}\right.\)

Vậy: \(x\in\left\{-5;-17\right\}\)

4) Ta có: \(\left(-3x+18\right)\left(-5x-10\right)=0\)

\(\Leftrightarrow\left[{}\begin{matrix}-3x+18=0\\-5x-10=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}-3x=-18\\-5x=10\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=6\\x=-2\end{matrix}\right.\)

Vậy: \(x\in\left\{6;-2\right\}\)

Bài nay ta có hai vế bạn hãy đặt giả sử một trong hai vế bằng 0 rồi giải phương trình cho mỗi vế bằng o

3.

\(\dfrac{1}{2}-\dfrac{1}{2}cos2x-3cos2x-2=0\)

\(\Leftrightarrow-7cos2x-3=0\)

\(\Rightarrow cos2x=-\dfrac{3}{7}\)

\(\Rightarrow2x=\pm arccos\left(-\dfrac{3}{7}\right)+k2\pi\)

\(\Rightarrow x=\pm\dfrac{1}{2}arccos\left(-\dfrac{3}{7}\right)+k\pi\)

4.

ĐKXĐ: \(x\ne\dfrac{k\pi}{2}\)

\(tanx+2tanx=0\)

\(\Rightarrow3tanx=0\)

\(\Rightarrow tanx=0\)

\(\Rightarrow x=k\pi\) (loại do ĐKXĐ)

Vậy pt đã cho vô nghiệm

1.

\(\Leftrightarrow1-sin^2x+sinx=0\)

\(\Leftrightarrow\left[{}\begin{matrix}sinx=\dfrac{1+\sqrt{5}}{2}>1\left(loại\right)\\sinx=\dfrac{1-\sqrt{5}}{2}\end{matrix}\right.\)

\(\Rightarrow\left[{}\begin{matrix}x=arcsin\left(\dfrac{1-\sqrt{5}}{2}\right)+k2\pi\\x=\pi-arcsin\left(\dfrac{1-\sqrt{5}}{2}\right)+k2\pi\end{matrix}\right.\) (\(k\in Z\))

2.

\(2cos^2x-\left(2cos^2x-1\right)+cosx=0\)

\(\Leftrightarrow cosx+1=0\)

\(\Leftrightarrow cosx=-1\)

\(\Leftrightarrow x=\pi+k2\pi\) (\(k\in Z\))

a) Học sinh thực hành.

b)

c) Các phép tính sai là:

8 : 1 = 1. Sửa: 8 : 1 = 8.

2 : 0 = 0. Sửa: 0 : 2 = 0.

3 : 0 = 0. Sửa: 0 : 3 = 0.

Bài 1:

$2xy=(x+y)^2-(x^2+y^2)=4^2-10=6\Rightarrow xy=3$ 

$M=x^6+y^6=(x^3+y^3)^2-2x^3y^3$

$=[(x+y)^3-3xy(x+y)]^2-2(xy)^3=(4^3-3.3.4)^2-2.3^3=730$

Bài 2:
$8x^3-32y-32x^2y+8x=0$

$\Leftrightarrow (8x^3+8x)-(32y+32x^2y)=0$

$\Leftrightarrow 8x(x^2+1)-32y(1+x^2)=0$

$\Leftrightarrow (8x-32y)(x^2+1)=0$
$\Rightarrow 8x-32y=0$ (do $x^2+1>0$ với mọi $x$)

$\Leftrightarrow x=4y$

Khi đó:

$M=\frac{3.4y+2y}{3.4y-2y}=\frac{14y}{10y}=\frac{14}{10}=\frac{7}{5}$

Bài cuối $x^21$ không rõ. Bạn xem lại.

\(1) \sqrt{9a^2.b^2}\)=3ab

\(2) \sqrt{3a}.\sqrt{27a}=\sqrt{3a}.3\sqrt{3a}=9a\)

\(3) \sqrt{3a^5}.12a=12\sqrt{3a^7}\)

\(4) \sqrt{5a}.\sqrt{45a}-3a=15a-3a=12a\)

\(5) \sqrt{3+\sqrt{a}}.\sqrt{3-\sqrt{a}}=\sqrt{(3+\sqrt{a}).(3-\sqrt{a})} =\sqrt{9-a} \)

\(6) \sqrt{3+\sqrt{5}}.\sqrt{3\sqrt{5}} =\sqrt{\sqrt{3\sqrt{5}}.(3+\sqrt{5})} =\sqrt{9+\sqrt{15}}\)

1) \(\sqrt{9a^2b^2}=3ab\)

2) \(\sqrt{3a}\cdot\sqrt{27a}=9a\)

4) \(\sqrt{5a}\cdot\sqrt{45a}-3a=15a-3a=12a\)