Cho ΔABC có góc A=900, góc B=540. Trên cạnh AC lấy điểm D sao cho góc DBC=180. So sánh BD và AC

Những câu hỏi liên quan
Cho tam giác ABC có góc A=90 độ,góc B=54 độ.Trên cạnh AC lấy điểm D sao cho góc DBC=18 độ.So sánh BD và AC.
https://hoc24.vn/hoi-dap/tim-kiem?q=Cho+tam+gi%C3%A1c+ABC+c%C3%B3+g%C3%B3c+A=90+%C4%91%E1%BB%99,g%C3%B3c+B=54+%C4%91%E1%BB%99.Tr%C3%AAn+c%E1%BA%A1nh+AC+l%E1%BA%A5y+%C4%91i%E1%BB%83m+D+sao+cho+g%C3%B3c+DBC=18+%C4%91%E1%BB%99.So+s%C3%A1nh+BD+v%C3%A0+AC.++Gi%C3%BAp+mik+vs+%C4%91ang+c%E1%BA%A7n+g%E1%BA%A5p!!!&id=171276
Đúng 2
Bình luận (1)
Xem thêm câu trả lời
Cho ΔABC có AB <AC . Tia phân giác góc A cắt BC ở D. Trên cạnh AC lấy điểm E sao cho AB =AE
So sánh BD và DC
Cho ΔABC có AB
So sánh BD và DC
Đề thiếu mk ko làm được
Cho tam giác ABC, góc A = 90, góc B = 54. trên cạnh AC lấy điểm D sao cho góc DBC = 18. CMR: BD < AC
Cho tam giác ABC có góc A=90 độ, góc B=54 độ. Trên cạnh AC lấy điểm D sao cho góc DBC=18 độ. Chứng minh rằng BD<AC
Cho tam giác ABC có ∠ABC= 55 0 , trên cạnh AC lấy điểm D (D không trùng với A và C)
Tính số đo của góc (DBC, biết số đo góc ∠ABD= 30 0
Từ B dựng ti Bx sao cho góc ∠DBx= 90 0 . Tính số đo góc ∠ABx
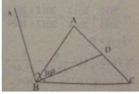
Tia BD nằm giữa hai tia BA và BC nên
∠ABC = ∠ADB + ∠DBC ; ∠DBC =∠ABC - ∠ADB
∠DBC = 55 0 - 30 0 = 25 0
Xét hai trường hợp
Trường hợp 1: Tia Bx và BD nằm trên
hai nửa mặt phẳng đối nhau có bờ là AB.
Ta có∠ABx = ∠DBx - ∠DBA= 90 0 - 30 0 = 60 0
Trường hợp 2: Tia Bx và BD nằm cùng nửa mặt phẳng đối nhau có bờ là AB.
Ta có ∠ABx = ∠DBx + ∠DBA= 90 0 + 30 0 = 120 0
Đúng 0
Bình luận (0)
Cho tam giác ABC vuông tại A , có góc B = 54 độ . Trên cạnh AC lấy điểm D sao cho góc DBC = 18 độ. CMR: BD < AC
Tam giác ABC có: góc BAC+góc ABC+góc ACB=180o (tổng 3 góc trong tam giác)
<=> 90o+54o+góc ACB=180o <=> góc ACB=36o
Góc ACB=36o<góc ABC=54o nên BD<AC (đpcm)
Đúng 0
Bình luận (0)
Cho ΔABC , góc A =90 độ , góc B=60độ .
a, So sánh AD và BD
b, Trên BC lấy D sao cho BD=AB . Qua D dựng đường vuông góc với BC cắt tia đối của AB tại E . Chứng minh : ΔABC=ΔDBE
c, H là giao điểm của AC và ED . Chứng minh : BH là phân giác của góc ABC
d, Qua B vẽ đường thẳng vuông góc AB cắt ED tại K . Chứng minh : ΔHBK đều
b) Xét ΔABC vuông tại A và ΔDBE vuông tại D có
AB=BD(gt)
\(\widehat{ABC}\) chung
Do đó: ΔABC=ΔDBE(cạnh góc vuông-góc nhọn kề)
c) Xét ΔBAH vuông tại A và ΔBDH vuông tại D có
BH chung
BA=BD(gt)
Do đó: ΔBAH=ΔBDH(Cạnh huyền-cạnh góc vuông)
Suy ra: \(\widehat{ABH}=\widehat{DBH}\)(hai góc tương ứng)
hay BH là tia phân giác của \(\widehat{ABC}\)
d) Ta có: BH là tia phân giác của \(\widehat{ABC}\)(cmt)
nên \(\widehat{ABH}=\dfrac{\widehat{ABC}}{2}=\dfrac{60^0}{2}=30^0\)
Ta có: \(\widehat{ABH}+\widehat{HBK}=90^0\)
\(\Leftrightarrow\widehat{HBK}+30^0=90^0\)
hay \(\widehat{HBK}=60^0\)
Xét ΔCHD vuông tại D và ΔCBA vuông tại A có
\(\widehat{ACB}\) chung
Do đó: ΔCHD\(\sim\)ΔCBA(g-g)
Suy ra: \(\widehat{CHD}=\widehat{CBA}\)(hai góc tương ứng)
\(\Leftrightarrow\widehat{CHD}=60^0\)
mà \(\widehat{CHD}=\widehat{HKB}\)(hai góc so le trong, BK//AC)
nên \(\widehat{HKB}=60^0\)
Xét ΔHBK có
\(\widehat{HKB}=60^0\)(cmt)
\(\widehat{HBK}=60^0\)(cmt)
Do đó: ΔHBK đều(Dấu hiệu nhận biết tam giác đều)
Đúng 0
Bình luận (1)
Cho ABC có Â = 900 . Tia phân giác BD của góc B(D thuộc AC). Trên cạnh BC lấy điểm E sao cho BE = BA. a) So sánh AD và DE b) Chứng minh: goc EDC= goc ABC c) Chứng minh : AE BD
cho góc nhọn xAy. Trên cạnh Ax lấy 2 điểm B và C sao cho AB=4cm; AC=6cm. Trên cạnh Ay lấy 2 điểm D và E sao cho AD=2cm; AE=12cm. Tia phân giác của góc xAy cắt BD tại I và cắt CE tại k.
a. so sánh AD/AB và AE/AC
b. so sánh góc ACE và góc ADB
c. cm: AI.KE=AK.IB
d. cho EC =10cm. Tính BD,DI
e. cm; KE.KC=9IB.ID
a/ Ta có: AD=2cm, AB=4cm, AE=12cm, AC=6cm
\(=>\left\{{}\begin{matrix}\dfrac{AD}{AB}=\dfrac{2}{4}=\dfrac{1}{2}\\\dfrac{AE}{AC}=\dfrac{12}{6}=2\end{matrix}\right.\)
\(=>\dfrac{AE}{AC}>\dfrac{AD}{AB}\)
Đúng 0
Bình luận (0)
a/ Ta có: AD=2cm, AB=4cm, AE=12cm, AC=6cm
=>AEAC>ADAB
Đúng 0
Bình luận (0)




















