Vẽ tam giác ABC có BC = 4 cm, \(\widehat{B}\) = 70o , \(\widehat{A}\) = 50o. Và nêu cách vẽ

Những câu hỏi liên quan
Vẽ tam giác ABC có BC = 4cm, \(\widehat{B}=70^o,\widehat{A}=50^o\)
Nêu cách vẽ dùm tớ luôn <3
HÌNH CHUẨN 100% MK DÙNG THƯỚC VÀ THƯỚC ĐO GÓC ĐỂ ĐO ĐÓ
(ĐO TRÊN MÀN HÌNH MÁY TÍNH)
Cách vẽ
Do góc B=70o, góc A=50o nên góc C=60o
B1: vễ đoạn thẳng BC dài 4 cm
B2: Từ B kẻ tia Bx sao cho góc B=70o
từ C kẻ tia Cy sao cho góc C=60o
Tia Bx, Cy cắt nhau tại A, ta đc tam giác ABC thỏa mãn đề bài
TK MK NHA BN
***** CHÚC BẠN HỌC GIỎI*****
Đúng 0
Bình luận (0)
Cách vẽ:
B1: Vẽ góc xÂy = 50*
B2: Trên Ax lấy điểm B, sau đó vẽ góc B = 70* kéo dài cắt Ay tại C
=> Ta có tam giác ABC thỏa mãn
Đúng 0
Bình luận (0)
Cho hai tam giác ABC và A’B’C’ (Hình 57) có: \(\widehat A = \widehat {A'} = 60^\circ \), AB = A’B’ = 3 cm, \(\widehat B = \widehat {B'} = 45^\circ \). Bằng cách đếm số ô vuông, hãy so sánh BC và B’C’. Từ đó có thể kết luận được hai tam giác ABC và A’B’C’ bằng nhau hay không?
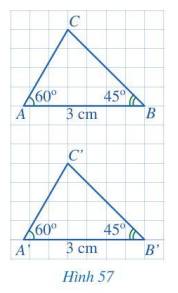
BC = B’C’ = 4 (đường chéo của 4 ô vuông).
Tam giác ABC và tam giác A’B’C’ có: BC = B’C’, AB = A’B’, \(\widehat B = \widehat {B'}\).
Vậy \(\Delta ABC = \Delta A'B'C'\)(c.g.c)
Đúng 0
Bình luận (0)
Bài 1 :a, Vẽ hình tam giác ABC. AB3 cm ,AC 4 cm, BC 5cm. Nêu cách vẽ.b, Đo các góc của tam giác ABC.Bài 2: Trên cùng nửa mp bờ chứa tia Ox. Vẽ các tia Oy, Oz sao cho widehat{xOy} 40 độ; widehat{xOz} 110 độ.a, Chứng tỏ tia Oy nằm giữa Ox, Oz.b, Ox là tia đối của tia Ox. Tính widehat{xOz}c, Tia Ox có là tia phân giác của widehat{xOy} không? Vì sao ?Bài 3: Cho Afrac{x+3}{x+2}.Tìm x nguyên để có giá trị nguyên.Giúp mik với nha, cảm ơn trước nha!
Đọc tiếp
Bài 1 :
a, Vẽ hình tam giác ABC. AB=3 cm ,AC= 4 cm, BC= 5cm. Nêu cách vẽ.
b, Đo các góc của tam giác ABC.
Bài 2: Trên cùng nửa mp bờ chứa tia Ox. Vẽ các tia Oy, Oz sao cho \(\widehat{xOy}\) = 40 độ; \(\widehat{xOz}\) =110 độ.
a, Chứng tỏ tia Oy nằm giữa Ox, Oz.
b, Ox' là tia đối của tia Ox. Tính \(\widehat{x'Oz}\)
c, Tia Ox có là tia phân giác của \(\widehat{xOy}\) không? Vì sao ?
Bài 3: Cho \(A=\frac{x+3}{x+2}\).Tìm x nguyên để có giá trị nguyên.
Giúp mik với nha, cảm ơn trước nha!
cho tam giác ABC cón\(^{\widehat{A}}=60^0,AB=AC\) đg cao BH(H thuôc AC)
a) so sánh \(\widehat{ABC}\)và\(\widehat{ACB}\),tính \(\widehat{ABH}\)
b)vẽ AD là tia p/g của góc A(D thuộc BC) vẽ BI vuông góc với AD tại I. CM tam giác AIB=tam giác BHA
c)tia BI cắt AC ở E .CM tam giác ABE đều
d) CM DC>DB
a) Em hãy trình bày các bước dùng phần mềm GeoGebra để vẽ tam giác ABC có:
AB = 6 cm, \(\widehat {BAC} = 60^\circ ,\widehat {ACB} = 70^\circ \)
b) Vẽ tam giác trên trong phần mềm GeoGebra và lưu thành một tệp có đuôi png
a) Xét tam giác ABC, áp dụng định lí tổng 3 góc trong tam giác, ta có:
\(\begin{array}{l}\widehat {BAC} + \widehat {ABC} + \widehat {ACB} = 180^\circ \\ \Rightarrow \widehat {ABC} = 180^\circ - (\widehat {BAC} + \widehat {ACB}) = 180^\circ - (60^\circ + 70^\circ ) = 50^\circ \end{array}\)
Bước 1: Vẽ AB = 6 cm
Bước 2: Vẽ \(\widehat {BAB'} = 60^\circ \)bằng cách:
Chọn công cụ Góc, nháy chuột lần lượt vào các điểm B, A ( theo chiều ngược kim đồng hồ) nhập số đo góc 60
Bước 3: Vẽ \(\widehat {ABA'} = 50^\circ \) bằng cách:
Chọn công cụ Góc, nháy chuột lần lượt vào các điểm A,B ( theo chiều kim đồng hồ) nhập số đo góc 50
Bước 4: Vẽ điểm C là giao điểm của AB’ và BA’
b)
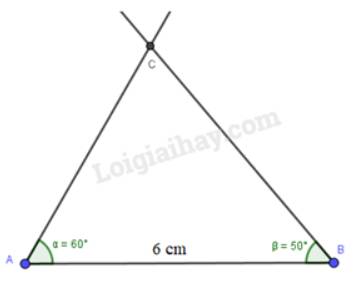
Nháy chuột vào Hồ sơ. Chọn xuất bản. Chọn hiển thị đồ thị dạng hình rồi lưu ảnh dạng png
Đúng 0
Bình luận (0)
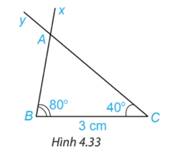
Vẽ đoạn thẳng \(BC = 3\;{\rm{cm}}\). Vẽ hai tia Bx và Cy sao cho \(\widehat {xBC} = {80^\circ },\widehat {yCB} = {40^\circ }\) như Hình 4.33.
Lấy giao điểm \(A\) của hai tia Bx và Cy, ta được tam giác ABC (H.4.33).
Cho tam giác ABC và tam giác DEF có góc A = 50o , góc E=70o,góc F= 60ocạnh AB=DE , AC=DF. CM tam giác ABC= tam giác DEF
\(\Delta DEF\) cho ta \(\widehat{D}+\widehat{E}+\widehat{F}=180^0\)
\(\Rightarrow\widehat{D}=180^0-\left(\widehat{E}+\widehat{F}\right)\)
\(\Rightarrow\widehat{D}=180^0-\left(70^0+60^0\right)=180^0-130^0=50^0\)
\(Xét\) \(\Delta ABCvà\Delta DEFcó\)
\(\widehat{A}=\widehat{D}\left(=50^0\right)\)
AB=DE
AC=DF
\(\Rightarrow\Delta ABC=\Delta DEF\left(c-g-c\right)\)
Vậy \(\Delta ABC=\Delta DEF\)
Đúng 1
Bình luận (0)
Cho hai tam giác ABC và A’B’C’ thỏa mãn: BC = B’C’ = 3 cm, \(\widehat B = \widehat {B'} = 60^\circ ,\widehat C = 50^\circ ,\widehat {A'} = 70^\circ \). Hai tam giác ABC và A’B’C’ có bằng nhau không? Vì sao?
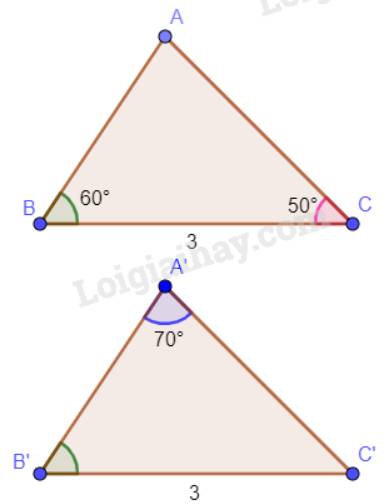
Tổng ba góc trong một tam giác bằng 180°. Vậy trong tam giác A’B’C’ có \(\widehat {C'} = 180^\circ - 70^\circ - 60^\circ = 50^\circ \).
Xét hai tam giác ABC và A’B’C’ có:
\(\widehat B = \widehat {B'} = 60^\circ ;\)
BC = B’C’ ( = 3 cm)
\(\widehat C = \widehat {C'} = 50^\circ \)
Vậy \(\Delta ABC = \Delta A'B'C'\)(g.c.g)
Đúng 0
Bình luận (0)
Vẽ tam giác ABC có AB = 6 cm, \(\widehat {BAC} = 50^\circ ;\widehat {ABC} = 60^\circ \)













