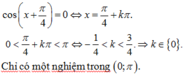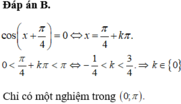số nghiệm của phương trình cos(frac{x}{2}+frac{pi}{4})0 thuộc khoảng (π;8π) là bao nhiêu ?
Đọc tiếp
số nghiệm của phương trình cos(\(\frac{x}{2}+\frac{\pi}{4}\))=0 thuộc khoảng (π;8π) là bao nhiêu ?
Những câu hỏi liên quan
6 tháng 12 2016 lúc 23:06
số nghiệm của phương trình \(\cos\left(\frac{x}{2}+\frac{\pi}{4}\right)=0\) thuộc khoảng \(\left(\pi;8\pi\right)\)là bao nhiêu ?
Có bao nhiêu giá trị nguyên của tham số m để phương trình 4cos^3 x - cos 2x + (m-3)cos x - 1 = 0 có đúng 4 nghiệm khác nhau thuộc khoảng (-π/2; π/2)
Xem chi tiết
6 tháng 12 2016 lúc 23:05
số nghiệm của phương trình \(\frac{\sin3x}{\cos x+1}=0\) thuộc đoạn \(\left[2\pi;4\pi\right]\)là bao nhiêu ?
Tìm số nghiệm thuộc khoảng ( 0 ; π ) của phương trình cos ( x + π 4 ) = 0.
A. 0
B. 1
C. 2
D. 3
Tìm số nghiệm thuộc khoảng
0
,
π
của phương trình
cos
x
+
π
4
0
A. 0 B. 1 C. 2 D. 3
Đọc tiếp
Tìm số nghiệm thuộc khoảng 0 , π của phương trình cos x + π 4 = 0
A. 0
B. 1
C. 2
D. 3
Trong các khoảng sau, m thuộc khoảng nào để phương trình sin^2 x-(2m+1) sin x.cos x + 2m cos^2 x = 0 có nghiệm thuộc khoảng (π/4 ; π/3)?
\(sin^2x-2m.sinx.cosx-sinx.cosx+2mcos^2x=0\)
\(\Leftrightarrow sinx\left(sinx-cosx\right)-2mcosx\left(sinx-cosx\right)=0\)
\(\Leftrightarrow\left(sinx-cosx\right)\left(sinx-2m.cosx\right)=0\)
\(\Rightarrow\left[{}\begin{matrix}sinx=cosx\\sinx=2m.cosx\end{matrix}\right.\)
\(\Rightarrow\left[{}\begin{matrix}tanx=1\\tanx=2m\end{matrix}\right.\)
Do \(tanx=1\) ko có nghiệm đã cho nên \(tanx=2m\) phải có nghiệm trên khoảng đã cho
\(\Rightarrow tan\left(\dfrac{\pi}{4}\right)< 2m< tan\left(\dfrac{\pi}{3}\right)\)
\(\Rightarrow1< 2m< \sqrt[]{3}\)
\(\Rightarrow m\in\left(\dfrac{1}{2};\dfrac{\sqrt{3}}{2}\right)\) (hoặc có thể 1 đáp án là tập con của tập này cũng được)
Đúng 0
Bình luận (0)
14 tháng 12 2016 lúc 20:45
tìm m để phương trình : \(\sin^6x+\cos^6x+2\cos3x\cos x-\cos4x+m=0\) có nghiệm thuộc đoạn \(\left[\frac{\pi}{4};\frac{\pi}{2}\right]\)
Tìm nghiệm của pt:
1) \(2cos2x+\sqrt{2}cos\frac{\pi}{4}=0\) thuộc khoảng (0;2π)
2) \(sin4x-cos4x+\sqrt{2}cos\left(4x-\frac{\pi}{4}\right)=\sqrt{6}\) thuộc khoảng (-π;5π)
1.
\(\Leftrightarrow2cos2x+\sqrt{2}.\frac{\sqrt{2}}{2}=0\)
\(\Leftrightarrow cos2x=-\frac{1}{2}\)
\(\Rightarrow\left[{}\begin{matrix}x=\frac{\pi}{3}+k\pi\\x=-\frac{\pi}{3}+k\pi\end{matrix}\right.\)
\(\Rightarrow x=\left\{\frac{\pi}{3};\frac{4\pi}{3};\frac{2\pi}{3};\frac{5\pi}{3}\right\}\)
2.
\(\Leftrightarrow sin4x-cos4x+sin4x+cos4x=\sqrt{6}\)
\(\Leftrightarrow2sin4x=\sqrt{6}\)
\(\Leftrightarrow sin4x=\frac{\sqrt{6}}{2}>1\)
Pt vô nghiệm
Đúng 0
Bình luận (0)
1) tìm m để phương trình 2sinx+mcosx1-m có nghiệm x thuộc left[-frac{pi}{2};frac{pi}{2}right]
2) tìm nghiệm của phương trình : sinx^24x+3.sin4x.cos4x-4.cos^24x0 khoảng left(0;frac{pi}{2}right)
3) tìm tất cả các nghiệm của phương trình cos5x.cosx cos4x.cos2x+ 3cos^2x+1 thuộc khoảng left(-pi;piright)
4) tìm tất cả các nghiệm trong khoảng (frac{2pi}{5};frac{6pi}{7}) của phương trình: sqrt{3}sin7x-cos7xsqrt{2}
Đọc tiếp
1) tìm m để phương trình 2sinx+mcosx=1-m có nghiệm x thuộc \(\left[-\frac{\pi}{2};\frac{\pi}{2}\right]\)
2) tìm nghiệm của phương trình : \(sinx^24x+3.sin4x.cos4x-4.cos^24x=0\) khoảng \(\left(0;\frac{\pi}{2}\right)\)
3) tìm tất cả các nghiệm của phương trình cos5x.cosx= cos4x.cos2x+ \(3cos^2x+1\) thuộc khoảng \(\left(-\pi;\pi\right)\)
4) tìm tất cả các nghiệm trong khoảng (\(\frac{2\pi}{5};\frac{6\pi}{7}\)) của phương trình: \(\sqrt{3}sin7x-cos7x=\sqrt{2}\)
1) Giải phương trình sau: frac{1}{2}sinxsinfrac{x}{2}.cos^2frac{x}{2} (*)
2) Trung bình cộng của GTLN và GTNN của hàm số y -sin^2x-4sinx+2.
3) Tìm giá trị của m để phương trình (m + 1)sin2x + 2cos2x 2m vô nghiệm.
4) Tìm tổng các nghiệm thuộc khoảng (0;101) của phương trình sin^4frac{x}{2}+cos^4frac{x}{2}1-2sinx.
5) Tìm nghiệm thuộc 0 x π của phương trình sin2x-frac{1}{2}.
6) Tìm nghiệm thuộc 0 ≤ x ≤ 2π của phương trình sqrt{2}cosleft(x+frac{pi}{3}right)1.
7) Tìm nghiệm của phương trì...
Đọc tiếp
1) Giải phương trình sau: \(\frac{1}{2}sinx=sin\frac{x}{2}.cos^2\frac{x}{2}\) (*)
2) Trung bình cộng của GTLN và GTNN của hàm số y = \(-sin^2x-4sinx+2\).
3) Tìm giá trị của m để phương trình (m + 1)sin2x + 2cos2x = 2m vô nghiệm.
4) Tìm tổng các nghiệm thuộc khoảng (0;101) của phương trình \(sin^4\frac{x}{2}+cos^4\frac{x}{2}=1-2sinx\).
5) Tìm nghiệm thuộc 0 < x < π của phương trình \(sin2x=-\frac{1}{2}\).
6) Tìm nghiệm thuộc 0 ≤ x ≤ 2π của phương trình \(\sqrt{2}cos\left(x+\frac{\pi}{3}\right)=1\).
7) Tìm nghiệm của phương trình sin(x + 17 độ).cos(x - 22 độ) + cos(x + 17 độ).sin(x - 22 độ) = \(\frac{\sqrt{2}}{2}\) thỏa điều kiện x ∈ (0 độ; 90 độ).
8) Cho ΔABC có các góc A, B, C thỏa mãn sinA.sinB.sinC = \(\frac{3\sqrt{3}}{8}\) . Chứng minh ΔABC đều.
