cho hình bên biết \(_{\widehat{ }A1}\) + \(\overline{\widehat{C1}}\) = \(\widehat{ABC}\) chứng tỏ m// n
lam hộ milk nha milk dang can gap
1.Cho hình 16:
a) Cho biết \(Ax//Cy.So\) \(sánh \)\(\widehat{ABC}\) với \(\widehat{A}\) và \(\widehat{C}\)
b) Cho biết \(\widehat{ABC}\)=\(\widehat{A}\) và\(\widehat{C}\) . Chứng tỏ rằng \(Ax//\) Cy
1Tam giác ABC có \(\widehat{A}\)là góc tù \(\widehat{B}>\widehat{C}\). So sánh độ dài các canhj của tam giác
2 Tam giác ABC, AB=5cm; BC=6cm; AC=7cm. Gọi \(\widehat{A1};\widehat{B1};\widehat{C1}\)theo thứ tự là góc ngoài tại đỉnh A;B;C của tam giác đó. So sánh \(\widehat{A1;}\widehat{B1};\widehat{C1}\)
CÁC CẬU ƠI GIÚP TỚ VS NHA. NHANH LÊN HUHUHU
Bài 1: Cho hình vẽ, biết \(n\perp AB\) tại B, \(\widehat{F_1}\)=\(120^o\).
a) Chứng tỏ m//n.
b) Tính \(\widehat{E_1}\).
c) Chứng tỏ \(m\perp AB\). Vì sao?
toán lớp 7
bài 1 tính các góc của \(\Delta ABC\)
a, \(\widehat{3A}=\widehat{4B};\widehat{A}-\widehat{B}=20°\) b,\(\widehat{B}-\widehat{C}=10°\) Và \(\widehat{C}-\widehat{A}=10°\)
giúp mik với mik dang can gap
góc A - góc B= 20o nên 4 lần góc A trừ 4 lần góc B bằng 80o.
mà 4 lần góc B bằng 3 lần góc A nên 4 lần góc A trừ 3 lần góc A bằng 80o.
Vậy góc A =80o góc B= 60o.
Cho \(\Delta\)ABC , vẽ đường thẳng M sao cho \(\widehat{BAM}\) bằng và so le trong với \(\widehat{B}\), vẽ đường thẳng N sao cho \(\widehat{CAN}\)bằng và so le trong với \(\widehat{C}\).Chứng tỏ rằng M,A,N thẳng hàng
Ta có: \(\widehat{BAM}=\widehat{B}\)
mà hai góc này ở vị trí so le trong
nên AM//BC
Ta có: \(\widehat{CAN}=\widehat{C}\)
mà hai góc này ở vị trí so le trong
nên AN//BC
Ta có: AM//BC
AN//BC
AM,AN có điểm chung là A
Do đó: A,M,N thẳng hàng
Bài 1: Cho hình vẽ, biết m\(\perp\)AB tại A, \(n\perp AB\) tại B, \(\widehat{F_1}\)=\(120^o\).
a) Chứng tỏ m//n.
b) Tính \(\widehat{E_1}\).
Giúp mik làm bài này với ạ. Mik cảm ơn!!!
Bài 4:Cho hình vẽ, biết a\(\perp\)MP tại M, \(b\perp NQ\) tại Q, \(\widehat{N_1}\)=\(65^O\).
a) Chứng tỏ a//b.
b) Tính \(\widehat{M_1}\)=?
ta có : a \(\perp\) P và b \(\perp\) Q \(\Rightarrow\)a//b
M1 và N1 là cặp góc trong cùng phía bù nhau
\(\Rightarrow\)M1= \(^{180^0}\)- N1= 180- \(65^0\)= 115
a) Trong Hình 20a, cho biết \(\widehat N = \widehat E,\widehat M = \widehat D,MP = 18m,DF = 24m,\)\(EF = 32m,\)\(NP = a + 3\left( m \right)\). Tìm \(a\).
b) Cho \(ABCD\) là hình thang \(\left( {AB//CD} \right)\) (Hình 20b).
Chứng minh rằng \(\Delta AMB\backsim\Delta CMD\). Tìm \(x,y\).

a) Xét tam giác \(MNP\) tam giác \(DEF\) ta có:
\(\widehat M = \widehat D\) (giả thuyết)
\(\widehat N = \widehat E\) (giả thuyết)
Do đó, \(\Delta MNP\backsim\Delta DEF\) (g.g)
Suy ra, \(\frac{{MP}}{{DF}} = \frac{{NP}}{{EF}} \Rightarrow \frac{{18}}{{24}} = \frac{{a + 2}}{{32}} \Rightarrow a + 2 = \frac{{18.32}}{{24}} = 24 \Leftrightarrow a = 24 - 2 = 22\).
Vậy \(a = 22m\).
b) Vì \(ABCD\) là hình thang nên \(AB//CD\).
Vì \(AB//CD \Rightarrow \widehat {ABM} = \widehat {MDC}\) (hai góc so le trong) và \(AB//CD \Rightarrow \widehat {BAM} = \widehat {MCD}\) (hai góc so le trong)
Xét tam giác \(AMB\) và tam giác \(CMD\) có:
\(\widehat {ABM} = \widehat {MDC}\) (chứng minh trên)
\(\widehat {BAM} = \widehat {MCD}\) (chứng minh trên)
Do đó, \(\Delta AMB\backsim\Delta CMD\) (g.g).
Ta có:
\(\frac{{AM}}{{CM}} = \frac{{BM}}{{DM}} = \frac{{AB}}{{CD}} \Leftrightarrow \frac{6}{{15}} = \frac{y}{{10}} = \frac{8}{x}\).
Ta có: \(\frac{6}{{15}} = \frac{y}{{10}} \Rightarrow y = \frac{{10.6}}{{15}} = 4\)
\(\frac{6}{{15}} = \frac{8}{x} \Rightarrow x = \frac{{8.15}}{6} = 20\).
Vậy \(x = 20;y = 4\).
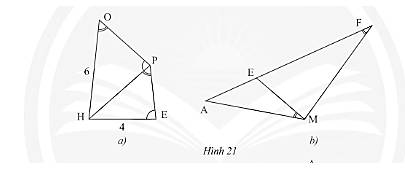
a) Trong Hình 21a, cho biết \(\widehat {HOP} = \widehat {HPE},\widehat {HPO} = \widehat {HEP},OH = 6cm\) và \(HE = 4cm\). Tính độ dài đoạn thẳng \(HP\).
b) Trong Hình 21b, cho biết \(\widehat {AME} = \widehat {AFM}\). Chứng minh rằng \(A{M^2} = AE.AF\).
a) Xét tam giác \(OPH\) tam giác \(PEH\) ta có:
\(\widehat {HOP} = \widehat {HPE}\) (giả thuyết)
\(\widehat {OPH} = \widehat {PEH}\) (giả thuyết)
Do đó, \(\Delta OPH\backsim\Delta PEH\) (g.g)
Suy ra, \(\frac{{PH}}{{EH}} = \frac{{OH}}{{PH}} \Rightarrow P{H^2} = OH.EH = 4.6 \Rightarrow P{H^2} = 24 \Leftrightarrow PH = \sqrt {24} = 2\sqrt 6 \).
Vậy \(PH = 2\sqrt 6 \).
b) Xét tam giác \(AME\) tam giác \(AFM\) ta có:
\(\widehat {AME} = \widehat {AFM}\) (giả thuyết)
\(\widehat A\) chung
Do đó, \(\Delta AME\backsim\Delta AFM\) (g.g)
Suy ra, \(\frac{{AM}}{{AF}} = \frac{{AE}}{{AM}} \Rightarrow A{M^2} = AF.AE\) (điều phải chứng minh).
Biết \(\widehat{xAB}=125°,\widehat{ABC}=100°,\widehat{BCy}=130°\) . Chứng tỏ rằng hai đường thẳng Ax và Cy cắt nhau