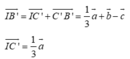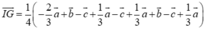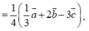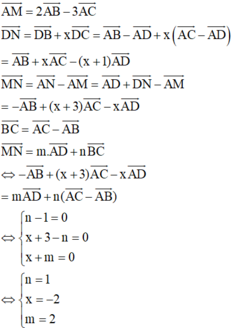Cho tam giác ABC có g là trọng tâm.gọi M,N là các điểm xác định bởi AM=2AB ,AN=2/5AC. phần tích véc tơ GM theo véc tơ GA và GB

Những câu hỏi liên quan
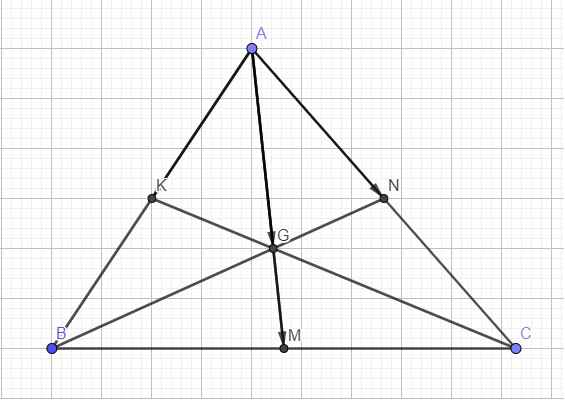
Cho tam giác ABC có 3 trung tuyến AM,BN,CK và trọng tâm G. Chứng minh:
a/véc tơ AM + véc tơ BN + véc tơ CK = véc tơ 0 ( đã xong )
b/ véc tơ GM + véc tơ GN + véc tơ GK = véc tơ 0 ( đã xong )
c/ 3.véc tơ AG = 2.(véc tơ AK + véc tơ AN )
Làm giúp mình câu c thôi ạ :(
Theo tính chất trọng tâm ta có: \(\overrightarrow{AG}=\dfrac{2}{3}\overrightarrow{AM}\)
Mặt khác AM là trung tuyến nên: \(\overrightarrow{AM}=\dfrac{1}{2}\overrightarrow{AB}+\dfrac{1}{2}\overrightarrow{AC}\)
\(\Rightarrow\overrightarrow{AG}=\dfrac{2}{3}\left(\dfrac{1}{2}\overrightarrow{AB}+\dfrac{1}{2}\overrightarrow{AC}\right)\Rightarrow3\overrightarrow{AG}=\overrightarrow{AB}+\overrightarrow{AC}\) (1)
K là trung điểm AB, N là trung điểm AC nên: \(\left\{{}\begin{matrix}\overrightarrow{AK}=\dfrac{1}{2}\overrightarrow{AB}\\\overrightarrow{AN}=\dfrac{1}{2}\overrightarrow{AC}\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}\overrightarrow{AB}=2\overrightarrow{AK}\\\overrightarrow{AC}=2\overrightarrow{AN}\end{matrix}\right.\) (2)
(1);(2) \(\Rightarrow3\overrightarrow{AG}=2\left(\overrightarrow{AK}+\overrightarrow{AN}\right)\)
Đúng 0
Bình luận (0)
Cho lăng trụ tam giác ABC.A’B’C’. Đặt
A
A
→
a
⇀
,
A
B
→
b
→
,
A
C
→
c
→
. Gọi I là điểm thuộc CC’ sao cho...
Đọc tiếp
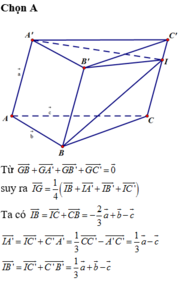
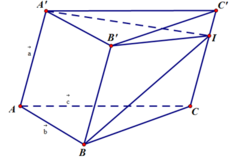
Cho lăng trụ tam giác ABC.A’B’C’. Đặt A A ' → = a ⇀ , A B → = b → , A C → = c → . Gọi I là điểm thuộc CC’ sao cho C ' I → = 1 3 C ' C → , điểm G thỏa mãn G B → + G A ' → + G B ' → + G C ' → = 0 → . Biểu diễn véc tơ I G → qua véc tơ a → , b → , c → . Trong các khẳng định sau, khẳng định nào là khẳng định đúng
A. I G → = 1 4 1 3 a → + 2 b → - 3 c →
B. I G → = 1 3 1 3 a → + 2 b → - 3 c →
C. I G → = 1 4 a → + 2 b → - 3 c →
D. I G → = 1 4 - 1 3 a → + 2 b → - 3 c →
Cho lăng trụ tam giác ABC.ABC. Đặt
A
A
→
a
→
,
A
B
→
b
→
,
A
C
→
c...
Đọc tiếp
Cho lăng trụ tam giác ABC.A'B'C'. Đặt A A ' → = a → , A B → = b → , A C → = c → . Gọi I là điểm thuộc CC' sao cho C ' I → = 1 3 C ' C → , điểm G thỏa mãn G B → + G A ' → + G B ' → + G C ' → = 0 → . Biểu diễn véc tơ I G → qua véc tơ a → , b → , c → . Trong các khẳng định sau, khẳng định nào là khẳng định đúng?
A. I G → = 1 4 1 3 a → + 2 b → - 3 c →
B. I G → = 1 3 1 3 a → + b → + 2 c →
C. I G → = 1 4 a → + b → - 2 c →
D. I G → = 1 4 a → + 1 3 b → - 2 c →
Cho tam giác ABC, M là trung điểm của AB, N ϵ AC sao cho NC=2NA. Xác định D sao cho 3 véc tơ AB + 4 lần véc tơ AC - 12 lần véc tơ KD = véc tơ 0
Cho hình bình hành ABCD tâm O. Gọi I là trung điểm của CD và G là trọng tâm của tam giác ABD. Phân tích véc tơ IG theo 2 véc tơ AB ; AD
Cho tứ diện ABCD và các điểm M,N xác định bởi
A
M
→
2
A
B
→
—
3
A
C
→
;
D
N
→
D...
Đọc tiếp
Cho tứ diện ABCD và các điểm M,N xác định bởi A M → = 2 A B → — 3 A C → ; D N → = D B → + x D C → Tìm x để ba véc tơ A D → , B C → , M N → đồng phẳng.
A. x=-1
B. x=-3
C. x=-2
D. x=2
Cho tứ diện ABCD và các điểm M,N xác định bởi
A
M
→
2
A
B
→
−
3
A
C
→
;
D
N
→
D
B
→
+...
Đọc tiếp
Cho tứ diện ABCD và các điểm M,N xác định bởi A M → = 2 A B → − 3 A C → ; D N → = D B → + x D C → . Tìm x để ba véc tơ A D → , B C → , M N → đồng phẳng
A.x= -1
B. x= -3
C. x= -2
D. x= 2
Đáp án C
A M → = 2 A B → − 3 A C → D N → = D B → + x D C → = A B → − A D → + x A C → − A D → = A B → + x A C → − ( x + 1 ) A D → M N → = A N → − A M → = A D → + D N → − A M → = − A B → + ( x + 3 ) A C → − x A D → B C → = A C → − A B →
Để 3 vectơ A D → , B C → , M N → đồng phẳng ⇔ ∃ m , n ∈ R sao cho :
A M → = 2 A B → − 3 A C → D N → = D B → + x D C → = A B → − A D → + x A C → − A D → = A B → + x A C → − ( x + 1 ) A D → M N → = A N → − A M → = A D → + D N → − A M → = − A B → + ( x + 3 ) A C → − x A D → B C → = A C → − A B → M N → = m . A D → + n B C → ⇔ − A B → + ( x + 3 ) A C → − x A D → = m A D → + n ( A C → − A B → ) ⇔ n − 1 = 0 x + 3 − n = 0 x + m = 0 ⇔ n = 1 x = − 2 m = 2
Đúng 0
Bình luận (0)
cho tam giác ABC trung tuyến AD. Gọi M là trung điểm AD, xét N ch bởi véc tơ AC bằng 3 lần véc tơ AN . CMR : B , M , N thẳng hàng
Cho tam giác ABC cố định . tìm điểm M hoặc tập hợp điểm M sao cho
véc tơ MA + 3 véc tơ MB - 2 véc tơ MC = véc tơ 0
3 véc tơ MA - véc tơ MB - 2 véc tơ MC = véc tơ 0