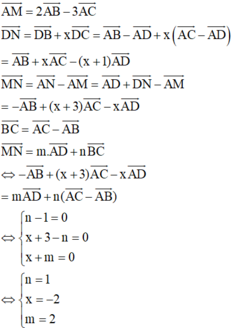Các câu hỏi tương tự
Cho hàm số y
x
3
+
2
m
+
1
x
2
+
3
m
x
+
2
có đồ thị (C) và điểm M(3;1). Tìm tham số m để đường thẳng d: y -x+2 cắt đồ thị (C) tại ba điểm phân biệt A(0;2),B,C sao cho tam giác MBC có diện tích bằng
2
6
A. m -2 B. m -2 hoặc m 3 C. m 3 D. K...
Đọc tiếp
Cho hàm số y = x 3 + 2 m + 1 x 2 + 3 m x + 2 có đồ thị (C) và điểm M(3;1). Tìm tham số m để đường thẳng d: y = -x+2 cắt đồ thị (C) tại ba điểm phân biệt A(0;2),B,C sao cho tam giác MBC có diện tích bằng 2 6
A. m = -2
B. m = -2 hoặc m = 3
C. m = 3
D. Không tồn tại m
Cho tứ diện ABCD. Trên ba cạnh AB, AC, AD lần lượt lấy các điểm B, C, D sao cho đường thẳng BCcắt đường thẳng BC tại K, đường thẳng CD cắt đường thẳng CD tại J, đường thẳng DB cắt đường thẳng DB tại I.a) Chứng minh ba điểm I, J, K thẳng hàng.b) Lấy điểm M ở giữa đoạn thẳng BD; điểm N ở giữa đoạn thẳng CD sao cho đường thẳng MN cắt đường thẳng BC và điểm F nằm bên trong tam giác ABC. Xác định thiết diện của tứ diện ABCD khi cắt bởi mặt phẳng (MNF).
Đọc tiếp
Cho tứ diện ABCD. Trên ba cạnh AB, AC, AD lần lượt lấy các điểm B', C', D' sao cho đường thẳng B'C'cắt đường thẳng BC tại K, đường thẳng C'D' cắt đường thẳng CD tại J, đường thẳng D'B' cắt đường thẳng DB tại I.
a) Chứng minh ba điểm I, J, K thẳng hàng.
b) Lấy điểm M ở giữa đoạn thẳng BD; điểm N ở giữa đoạn thẳng CD sao cho đường thẳng MN cắt đường thẳng BC và điểm F nằm bên trong tam giác ABC. Xác định thiết diện của tứ diện ABCD khi cắt bởi mặt phẳng (MNF).
Cho khối tứ diện ABCD. Lấy điểm M nằm giữa A và B, điểm N nằm giữa C và D. Bằng hai mặt phẳng (CDM) và (ABN), ta chia khối tứ diện đó thành bốn khối tứ diện nào sau đây ? A. MANC, BCDN, AMND, ABND. B. MANC, BCMN, AMND, MBND. C. ABCN, ABND, AMND, MBND. D. NACB, BCMN, ABND, MBND.
Đọc tiếp
Cho khối tứ diện ABCD. Lấy điểm M nằm giữa A và B, điểm N nằm giữa C và D. Bằng hai mặt phẳng (CDM) và (ABN), ta chia khối tứ diện đó thành bốn khối tứ diện nào sau đây ?
A. MANC, BCDN, AMND, ABND.
B. MANC, BCMN, AMND, MBND.
C. ABCN, ABND, AMND, MBND.
D. NACB, BCMN, ABND, MBND.
ho hình chóp tứ giác S . A B C D , M là một điểm trên cạnh S C , N là trên cạnh B C . Tìm giao điểm của đường thẳng S D với mặt phẳng ( A M N ) .
Cho các hàm số
f
(
x
)
x
3
+
b
x
2
+
c
x
+
d
(
C
)
g
(
x
)
x
2
−
3
x...
Đọc tiếp
Cho các hàm số
f ( x ) = x 3 + b x 2 + c x + d ( C )
g ( x ) = x 2 − 3 x − 1 .
a) Xác định b, c, d sao cho đồ thị (C) đi qua các điểm (1; 3), (−1; −3) và f′(1/3) = 5/3 ;
b) Viết phương trình tiếp tuyến của (C) tại điểm có hoành độ x 0 = 1 ;
c) Giải phương trình f′(sint) = 3;
d) Giải phương trình f′′(cost) = g′(sint);
e) Tìm giới hạn lim z → 0 f ' ' sin 5 z + 2 g ' sin 3 z + 3
cho hình chóp tứ giác S . A B C D , M là một điểm trên cạnh S C , N là trên cạnh sb . Tìm giao điểm của đường thẳng S D với mặt phẳng ( A M N ) .
Xem chi tiết
Trên mặt phẳng Oxy ta xét một hình chữ nhật ABCD với các điểm A(-2; 0), B(-2; 2), C(4; 2), D(4;0). Một con châu chấu nhảy trong hình chữ nhật đó tính cả trên cạnh hình chữ nhật sao cho chân nó luôn đáp xuống mặt phẳng tại các điểm có tọa độ nguyên( tức là điểm có cả hoành độ và tung độ đều nguyên). Tính xác suất để nó đáp xuống các điểm M(x; y) mà x + y 2. A.
3
7
.
B.
8
21
....
Đọc tiếp
Trên mặt phẳng Oxy ta xét một hình chữ nhật ABCD với các điểm A(-2; 0), B(-2; 2), C(4; 2), D(4;0). Một con châu chấu nhảy trong hình chữ nhật đó tính cả trên cạnh hình chữ nhật sao cho chân nó luôn đáp xuống mặt phẳng tại các điểm có tọa độ nguyên( tức là điểm có cả hoành độ và tung độ đều nguyên). Tính xác suất để nó đáp xuống các điểm M(x; y) mà x + y < 2.
A. 3 7 .
B. 8 21 .
C. 1 3 .
D. 4 7 .
cho tứ diện ABCD và điểm M nằm trong tứ diện, qua M dựng các mặt phẳng (a) song song (BCD), (b) song song (ACD), (c) song song (ABD), (d) song song (ABC). Biết (a) cắt AB tại E, (b) cắt BC tại F, (c) cắt CD tại P, (d) cắt AD tại Q
cmr: \(\sqrt{\dfrac{EA}{EB}}+\sqrt{\dfrac{FB}{FC}}+\sqrt{\dfrac{PC}{PD}}+\sqrt{\dfrac{QD}{QA}}\ge4\sqrt{3}\)
1. Cho hình bình hành ABCD có tâm O, Gọi M, N lần lượt là trung điểm của AB, AO.a) XĐ ảnh của tam giác AND qua phép tịnh tiến overrightarrow{OC}b)XĐ ảnh của tam giác AMN qua phép vị tự tâm O, tỉ số -22. trong mặt phẳng Oxy cho điểm M(1;-5),overrightarrow{v}left(-2,1right)đường thẳng d: x-4y+30,đường tròn left(Cright):left(x+2right)^2+left(y-1right)^25a) tìm tọa độ M là ảnh của M qua phép tịnh tiến vecto overrightarrow{v}b)Viết phương trình d là ảnh của d qua phép quay tâm O, góc quay ^{-90^o}c)...
Đọc tiếp
1. Cho hình bình hành ABCD có tâm O, Gọi M, N lần lượt là trung điểm của AB, AO.
a) XĐ ảnh của tam giác AND qua phép tịnh tiến \(\overrightarrow{OC}\)
b)XĐ ảnh của tam giác AMN qua phép vị tự tâm O, tỉ số -2
2. trong mặt phẳng Oxy cho điểm M(1;-5),\(\overrightarrow{v}=\left(-2,1\right)\)đường thẳng d: x-4y+3=0,
đường tròn \(\left(C\right):\left(x+2\right)^2+\left(y-1\right)^2=5\)
a) tìm tọa độ M' là ảnh của M qua phép tịnh tiến vecto \(\overrightarrow{v}\)
b)Viết phương trình d' là ảnh của d qua phép quay tâm O, góc quay \(^{-90^o}\)
c) tìm phương trình (C') là ảnh của (C) qua phép vị tự tâm O, tỉ số 2.
3.
Cho đường thẳng (d): x-5y-4=0. Viết phương trình đường thẳng (d') ảnh của (d) qua phép vị tự tâm O , góc 90o và phép vị tự tâm I(-2,3) tỉ số -3