BBieesn đổi hằng đẳng thức 

x²+4x+4

=x²+2.2x+2²

=(x+2)²

Ta có:

\(x^2+4x+4\)

\(=x^2+2.2x+2^2\)

\(=\left(x+2\right)^2\)

Ta có : x² + 4x + 4 = (x + 2)²

\(=\sqrt{3-2\sqrt{3}+1}=\sqrt{\left(\sqrt{3}-1\right)^2}=\left|\sqrt{3}-1\right|=\sqrt{3}-1\)

bạn vừa đăng câu này rồi mà

`4b^2+a^2+4ab`

`=(2b)^2+2.2b.a+a^2`

`=(a+2b)^2`

`-49-2a^4+14sqrt2a^2`

`=-(2a^4-14sqrt2a^2+49)`

`=-((sqrt2a^2)^2-2.sqrt2a^2.7+7^2)`

`=-(sqrt2a^2-7)^2`

\(a^2+4ab+4b^2=\left(a+2b\right)^2\)

\(-49-2a^4+14\sqrt{2a^2}=-\left(\sqrt{2a^2}-7\right)^2\)

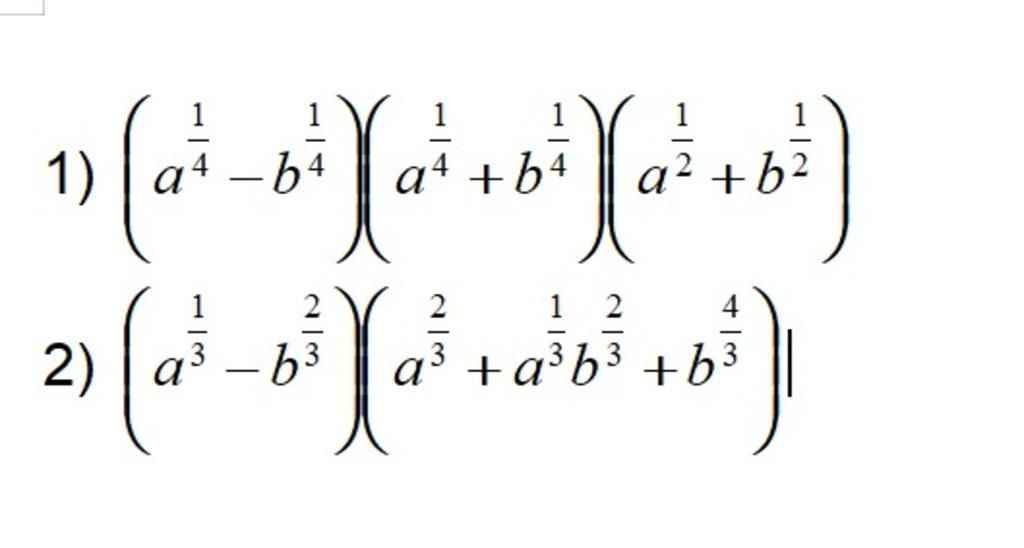
`1)(a^[1/4]-b^[1/4])(a^[1/4]+b^[1/4])(a^[1/2]+b^[1/2])`

`=[(a^[1/4])^2-(b^[1/4])^2](a^[1/2]+b^[1/2])`

`=(a^[1/2]-b^[1/2])(a^[1/2]+b^[1/2])`

`=a-b`

`2)(a^[1/3]-b^[2/3])(a^[2/3]+a^[1/3]b^[2/3]+b^[4/3])`

`=(a^[1/3]-b^[2/3])[(a^[1/3])^2+a^[1/3]b^[2/3]+(b^[2/3])^2]`

`=(a^[1/3])^3-(b^[2/3])^3`

`=a-b^2`

1. Ta có: \(\dfrac{x^7+x^6+x^5+x^4+x^3+x^2+x+1}{x^2-1}\)

\(=\dfrac{x^6\left(x+1\right)+x^4\left(x+1\right)+x^2\left(x+1\right)+\left(x+1\right)}{\left(x+1\right)\left(x-1\right)}\)

\(=\dfrac{\left(x+1\right)\left(x^6+x^4+x^2+1\right)}{\left(x+1\right)\left(x-1\right)}\)

\(=\dfrac{\left(x^6+x^4+x^2+1\right)}{\left(x-1\right)}\)

\(=\dfrac{x^4\left(x^2+1\right)+x^2+1}{x-1}\)

\(=\dfrac{\left(x^2+1\right)\left(x^4+1\right)}{x-1}\)

2.Ta có: \(\dfrac{x^2+y^2+z^2-2xy+2xz-2xz}{x^2-2xy+y^2-z^2}\)

\(=\dfrac{\left(x-y+z\right)^2}{\left(x-y\right)^2-z^2}=\dfrac{\left(x-y+z\right)\left(x-y+z\right)}{\left(x-y-z\right)\left(x-y+z\right)}=\dfrac{x-y+z}{x-y-z}\)

_Chúc bạn học tốt_

\(\text{1) }\dfrac{x^7+x^6+x^5+x^4+x^3+x^2+x+1}{x^2-1}\\ =\dfrac{\left(x^7+x^6\right)+\left(x^5+x^4\right)+\left(x^3+x^2\right)+\left(x+1\right)}{\left(x-1\right)\left(x+1\right)}\\ =\dfrac{x^6\left(x+1\right)+x^4\left(x+1\right)+x^2\left(x+1\right)+\left(x+1\right)}{\left(x-1\right)\left(x+1\right)}\\ =\dfrac{\left(x+1\right)\left(x^6+x^4+x^2+1\right)}{\left(x-1\right)\left(x+1\right)}\\ =\dfrac{x^6+x^4+x^2+1}{\left(x-1\right)}\\ \)

\(\text{2) }\dfrac{x^2+y^2+z^2-2xy+2xz-2yz}{x^2-2xy+y^2-z^2}\\ =\dfrac{\left(x^2-2xy+y^2\right)+\left(2xz-2yz\right)+z^2}{\left(x^2-2xy+y^2\right)-z^2}\\ =\dfrac{\left(x-y\right)^2+2z\left(x-y\right)+z^2}{\left(x-y\right)^2-z^2}\\ =\dfrac{\left(x-y+z\right)^2}{\left(x-y+z\right)\left(x-y-z\right)}\\ =\dfrac{x-y+z}{x-y-z}\)

\(x^2+10x+26+y^2+2y\)

\(=\left(x^2+10x+25\right)+\left(y^2+2y+1\right)\)

\(=\left(x+5\right)^2+\left(y+1\right)^2\)

\(\left(x+y+4\right)\left(x+y-4\right)\)

\(=\left(x+y\right)^2-16\)

\(=x^2+y^2+2xy-16\)

a, =(x^2 +10x+25) +(y^2 +2y+1)

    = (x+5)^2 +(y+1)^2

b, =(x+y)^2 -4^2

    = x^2 + 2xy+ y^2 -16

x²+10x+26+y²+2y=(x+5)²+(y+1)²

(x+y+4)(x+y-4)=(x+y)²-16