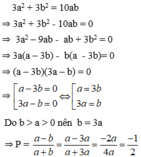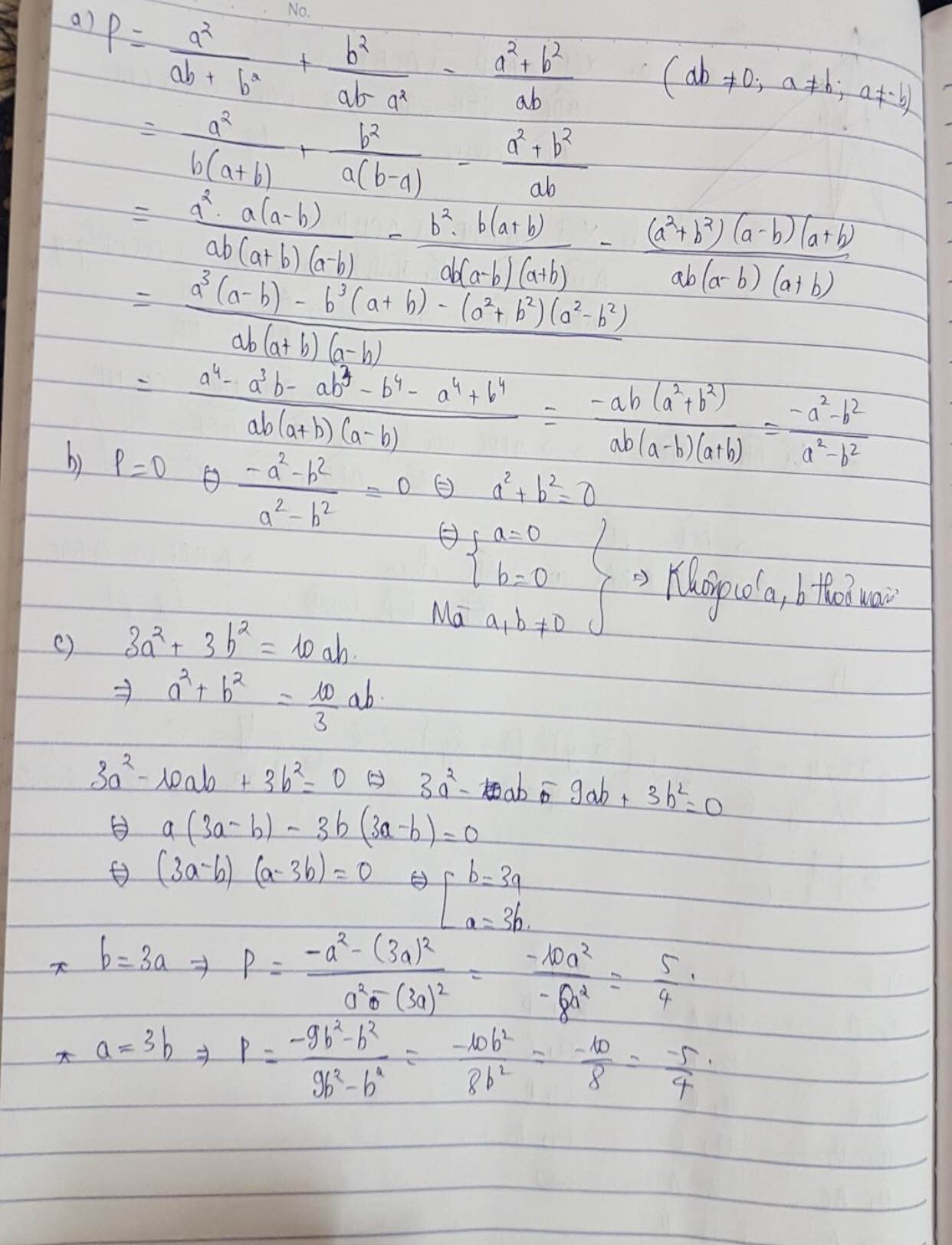Tìm giá trị nguyên của a để: 3a2 + 7a2 - 6 chia het cho 3a2 + 1

Những câu hỏi liên quan
1. Cho a, b là hai hằng số với | a |> 0. Nếu phương trình || x-a | -b | = 3 có ba nghiệm phân biệt x, hãy tìm giá trị của b
2. Cho a = 2009. Tìm giá trị của | 2a3-3a2-2a + 1 | + | 2a3-3a2-3a-2009 |
Cho a,b∈∈ N va 2a+b chia het cho 7 CM 3a2+10ab-8b2 chia het cho 49
Đặt 2a + b = 7k chia hết cho 7 => (2a + b)2 = 49k2 chia hết cho 49
(2a + b)2 = 4a2 + 4ab + b2 chia hết cho 49
4a2 + 4ab + b2 - (3a2 +10ab - 8b2) = a2 - 6ab +9b2 = (a - 3b)2
Ta có 2a + b chia hết cho 7 nên 3(2a + b) = 6a + 3b chia hết cho7
Ta có 6a + 3b + (a - 3b) = 7a chia hết cho 7 mà 6a + 3b chia hết cho 7 => a - 3b chia hết cho 7
a - 3b chia hết cho 7 => (a - 3b)2 chia hết cho 49
=> 4a2 + 4ab + b2 - (3a2 + 10ab - 8b2) chia hết cho 49
mà 4a2 + 4ab + b2 chia hết cho 49 => 3a2 + 10ab - 8b2 chia hết cho 49
Đúng 0
Bình luận (0)
Bài 1: Tìm giá trị nhỏ nhất hoặc lớn nhất của các biểu thức sau:a) A a4-2a3+3a2-4a+5b) B dfrac{x^2+4x-6}{3}c) C dfrac{4+5left|1-2xright|}{7}Bài 2: a) Tìm a sao cho x4-x3+6x2-x+a chia hết cho đa thức x2-x+5.b) Xác định hằng số a và b sao cho x4+ax2+b chia hết cho x2-x+1Bài 3: Tính giá trị của biểu thức: A x17-12x14+...-12x12+12x-1 với x11
Đọc tiếp
Bài 1: Tìm giá trị nhỏ nhất hoặc lớn nhất của các biểu thức sau:
a) A= a4-2a3+3a2-4a+5
b) B= \(\dfrac{x^2+4x-6}{3}\)
c) C= \(\dfrac{4+5\left|1-2x\right|}{7}\)
Bài 2:
a) Tìm a sao cho x4-x3+6x2-x+a chia hết cho đa thức x2-x+5.
b) Xác định hằng số a và b sao cho x4+ax2+b chia hết cho x2-x+1
Bài 3: Tính giá trị của biểu thức: A= x17-12x14+...-12x12+12x-1 với x=11
Cho 3 a 2 + 3 b 2 = 10 a b và b > a > 0. Tính giá trị của biểu thức P = a - b a + b
cho biểu thức A(2a/a+3-2/3-3a2+3/aa-9):a+1/a-3 (a khác -1;a khác +-3)a) Rút gọn Bb) Tính B với giá trị tuyệt đối của a 2c) tìm a thuộc Z để B thuộc ZGiúp em vs ạ em dag cần lời giải gấp
Đọc tiếp
cho biểu thức A=(2a/a+3-2/3-3a2+3/aa-9):a+1/a-3 (a khác -1;a khác +-3)
a) Rút gọn B
b) Tính B với giá trị tuyệt đối của a =2
c) tìm a thuộc Z để B thuộc Z
Giúp em vs ạ em dag cần lời giải gấp![]()
![]()
![]()
cho hàm số y=\(\dfrac{2x-1}{x+1}\) có tiệm cận đứng x=a, tiệm cận ngang y=b. Giá trị của biểu thức P=3a2-b là
\(\lim\limits_{x\rightarrow-1^+}\dfrac{2x-1}{x+1}=-\infty\Rightarrow x=-1\) là tiệm cận đứng
\(\lim\limits_{x\rightarrow+\infty}\dfrac{2x-1}{x+1}=2\Rightarrow y=2\) là tiệm cận ngang
\(\Rightarrow P=3.\left(-1\right)^2-2=1\)
Đúng 0
Bình luận (0)
Gọi M(a;b) là điểm thuộ
y
2
x
+
1
x
+
2
c đồ thị hàm số và có khoảng cách từ M đến đường thẳng d:y3x+6 nhỏ nhất. Tìm giá trị của biểu thức
T
3
a
2
+
b
2
. A. T4 B. T3 C. T9 D. T10
Đọc tiếp
Gọi M(a;b) là điểm thuộ y = 2 x + 1 x + 2 c đồ thị hàm số và có khoảng cách từ M đến đường thẳng d:y=3x+6 nhỏ nhất. Tìm giá trị của biểu thức T = 3 a 2 + b 2 .
A. T=4
B. T=3
C. T=9
D. T=10
Cho biểu thức:
P=\(\dfrac{a^2}{ab+b^2}+\dfrac{b^2}{ab-a^2}-\dfrac{a^2+b^2}{ab}\)
a) rút gọn P
b) có giá trị nào của a,b để P=0
c) tính giá trị của P biết a,b thỏa mãn điều kiện: 3a2+3b2= 10ab và a>b>0
\(P=\dfrac{a^2}{ab+b^2}+\dfrac{b^2}{ab-a^2}-\dfrac{a^2+b^2}{ab}\) (\(a\ne b;a\ne0;a\ne-b;b\ne0\))
\(=\dfrac{a^2}{b\left(a+b\right)}+\dfrac{b^2}{a\left(b-a\right)}-\dfrac{a^2+b^2}{ab}\)
\(=\dfrac{a^3\left(a-b\right)-b^3\left(a+b\right)-\left(a^2+b^2\right)\left(a+b\right)\left(a-b\right)}{ab\left(a+b\right)\left(a-b\right)}\)
\(=\dfrac{a^4-a^3b-b^3a-b^4-\left(a^2+b^2\right)\left(a^2-b^2\right)}{ab\left(a+b\right)\left(a-b\right)}\)
\(=\dfrac{a^4-a^3b-b^3a-b^4-\left(a^4-b^4\right)}{ab\left(a+b\right)\left(a-b\right)}\)
\(=\dfrac{-a^3b-b^3a}{ab\left(a+b\right)\left(a-b\right)}\)
\(=\dfrac{-ab\left(a^2+b^2\right)}{ab\left(a+b\right)\left(a-b\right)}=-\dfrac{a^2+b^2}{a^2-b^2}\).
b) -Ta có: \(P=0\)
\(\Leftrightarrow-\dfrac{a^2+b^2}{a^2-b^2}=0\)
\(\Leftrightarrow a^2+b^2=0\)
-Vì \(a^2\ge0;b^2\ge0\)
\(\Rightarrow a=0;b=0\) (không thỏa mãn điều kiện).
-Vậy không có giá trị nào của a,b để \(P=0\).
c)
Đúng 1
Bình luận (0)
Có tất cả bao nhiêu số nguyên của a để biểu thức T= log20 ( 12- 3a2) có nghĩa?
A. 1
B. 3.
C. 5
D. 7
Biểu thức T có nghĩa khi và chỉ khi 12- 3a2> 0 hay a2< 4
Do đó; - 2< a< 2
Kết hợp với a nguyên nên a
Vậy có 3 giá trị thỏa mãn.
Chọn B
Đúng 0
Bình luận (0)