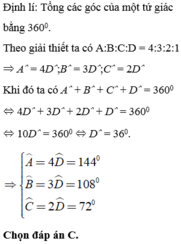Tính các góc của hình tứ giác ABCD.
A:B:C:D=1:2:3:4

Những câu hỏi liên quan
Cho tứ giác ABCD biết A:B:C:D=1:2:3:4
a. CMR: ABCD là hình thang
b. AD cắt BC tại E. Tính các góc của tam giác CDE
a)Từ A:B:C:D=1:2:3:4
=>\(\frac{A}{1}=\frac{B}{2}=\frac{C}{3}=\frac{D}{4}\) và A+B+C+D=3600
Áp dụng tính chất dãy tiwr số bằng nhau ta có:
\(\frac{A}{1}=\frac{B}{2}=\frac{C}{3}=\frac{D}{4}=\frac{A+B+C+D}{1+2+3+4}=\frac{360}{10}=36\)
=>A=36.1=360
B=36.2=720
C=36.3=1080
D=36.4=1440
=>A+D=360+1440=1800
Do A và D là 2 góc trong cùng phía =>AB//CD=>ABCD là hình thang
Ta có:CDE+CDA=1800=>1440+CDE=1800=>CDE=360
DCE+BCD=1800=>DCE+1080=1800=>DCE=720
Do CDE+DCE+DEC=1800
=>360+720+DEC=1800
=>DEC=720
Đúng 1
Bình luận (0)
Cho tứ giác ABCD biết A:B:C:D=1:2:3:4
a. CMR: ABCD là hình thang
b. AD cắt BC tại E. Tính các góc của tam giác CDE
a: Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:
\(\dfrac{a}{1}=\dfrac{b}{2}=\dfrac{c}{3}=\dfrac{d}{4}=\dfrac{a+b+c+d}{1+2+3+4}=\dfrac{360}{10}=36\)
Do đó: a=36; b=72; c=108; d=144
Vì a+d=180
nên ABCD là hình thang
b: góc EDC=180-144=36 độ
góc ECD=180-108=72 độ
góc E=180-36-72=72 độ
Đúng 0
Bình luận (0)
Cho tứ giác ABCD biết : A:B:C:D=1:2:3:4
a) Tính các góc của tứ giác
b) Chứng minh AB//CD
c) AD cắt BC tại E. Tính các góc của tam giác EDC
A^1=B^2=C^3=D^4" role="presentation" style="border:0px; box-sizing:inherit; direction:ltr; display:inline-table; float:none; font-size:18.08px; line-height:0; margin:0px; max-height:none; max-width:none; min-height:0px; min-width:0px; overflow-wrap:normal; padding:1px 0px; position:relative; white-space:nowrap; word-spacing:normal" class="MathJax_CHTML mjx-chtml">A^+B^+C^+D^1+2+3+4" role="presentation" style="border:0px; box-sizing:inherit; direction:ltr; display:inline-block; float:none; font-size:18.08px; line-height:0; margin:0px; max-height:none; max-width:none; min-height:0px; min-width:0px; overflow-wrap:normal; padding:1px 0px; position:relative; white-space:nowrap; word-spacing:normal" class="MathJax_CHTML mjx-chtml">360o10" role="presentation" style="border:0px; box-sizing:inherit; direction:ltr; display:inline-block; float:none; font-size:18.08px; line-height:0; margin:0px; max-height:none; max-width:none; min-height:0px; min-width:0px; overflow-wrap:normal; padding:1px 0px; position:relative; white-space:nowrap; word-spacing:normal" class="MathJax_CHTML mjx-chtml">=
=>=;=;=;=
b, Có +=+
=
mà 2 góc này ở vị trí slt
=>AB//CD
Cho tứ giác ABCD biết A:B:C:D=1:2:3:4
a)Tính các góc của tứ giác
b)CMR : AB//CD
c)Gọi giao điểm của AD và BC là E . Tính các góc tứ giác CDE
a: Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:
\(\dfrac{\widehat{A}}{1}=\dfrac{\widehat{B}}{2}=\dfrac{\widehat{C}}{3}=\dfrac{\widehat{D}}{4}=\dfrac{360^0}{10}=36^0\)
Do đó: \(\widehat{A}=36^0;\widehat{B}=72^0;\widehat{C}=108^0;\widehat{D}=144^0\)
b: ta có: \(\widehat{B}+\widehat{C}=180^0\)
mà hai góc này là hai góc ở vị trí trong cùng phía
nên AB//CD
Đúng 1
Bình luận (0)
cho tứ giác ABCD có A:B:C:D = 1:2:3:4
a ) tính các góc của tứ giác ABCD
b) chứng minh : AB//CD
c) gọi F là giao điểm của AB và CD .tính số đo của góc DCF
Số đo các góc của tứ giác ABCD theo tỷ lệ A:B:C:D 4:3:2:1. Số đo các góc theo thứ tự đó là? A.
120
0
;
90
0
;
72
0
;
36
0
B.
140
0
;
108
0
;
72
0
;
36
0
...
Đọc tiếp
Số đo các góc của tứ giác ABCD theo tỷ lệ A:B:C:D = 4:3:2:1. Số đo các góc theo thứ tự đó là?
A. 120 0 ; 90 0 ; 72 0 ; 36 0
B. 140 0 ; 108 0 ; 72 0 ; 36 0
C. 144 0 ; 108 0 ; 72 0 ; 36 0
D. Cả A, B, C đều sai.
Số đo các góc của tứ giác ABCD theo tỷ lệ A:B:C:D 4:3:2:1. Số đo các góc theo thứ tự đó là ? A.
120
0
;
90
0
;
60
0
;
30
0
. B.
140
0
;
105
0
;
70
0
;
35
0
....
Đọc tiếp
Số đo các góc của tứ giác ABCD theo tỷ lệ A:B:C:D = 4:3:2:1. Số đo các góc theo thứ tự đó là ?
A. 120 0 ; 90 0 ; 60 0 ; 30 0 .
B. 140 0 ; 105 0 ; 70 0 ; 35 0 .
C. 144 0 ; 108 0 ; 72 0 ; 36 0 .
D. Cả A, B, C đều sai.
cho tứ giác ABCD có A:B:C:D=7:5:4:2 a,tính các góc;b CMR : AB//CD
a: Xét tứ giác ABCD có
\(\widehat{A}+\widehat{B}+\widehat{C}+\widehat{D}=180^0\)
mà \(\dfrac{\widehat{A}}{7}=\dfrac{\widehat{B}}{5}=\dfrac{\widehat{C}}{4}=\dfrac{\widehat{D}}{2}\)
nên Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:
\(\dfrac{\widehat{A}}{7}=\dfrac{\widehat{B}}{5}=\dfrac{\widehat{C}}{4}=\dfrac{\widehat{D}}{2}=\dfrac{360^0}{18}=20^0\)
Do đó: \(\widehat{A}=140^0;\widehat{B}=100^0;\widehat{C}=80^0;\widehat{D}=40^0\)
b: Ta có: \(\widehat{B}+\widehat{C}=180^0\)
mà hai góc này là hai góc trong cùng phía
nên AB//CD
Đúng 0
Bình luận (1)
Cho tứ giác A:B:C:D=1:2:3:4
A)Tính các góc tứ giác
B)CM:AB//CD
C)AD cắt BC tại E.Tính các góc của tam giác EDC
a) Vì A: B:C:D = 1:2:3:4
=> A= B/2 = C/3=D/4
Áp dụng tính chất dãy tỉ số bằng nhau ta có:
A = 36 độ
B= 72 độ
C=108 độ
D= 144 độ
b) Ta có :
A + D = 36 + 144 = 180 độ(1)
B+C = 72 + 108 = 180 độ(2)
Từ (1) và (2) ta có:
=> AB //CD (dpcm)
c) Ta có :
CDE + ADC = 180 độ(kề bù)
=> CDE = 180 - 144 = 36
Ta có :
BCD + DCE = 180 độ ( kề bù)
=> DCE = 180 - 108 = 72
Xét ∆CDE ta có :
CDE + DCE + DEC = 180 ( tổng 3 góc trong ∆)
=> DEC = 180 - 72 - 36 = 72 độ