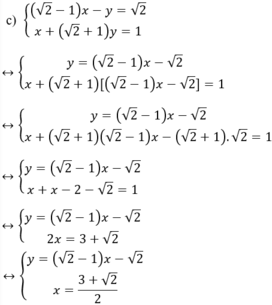\(\left\{{}\begin{matrix}x^2+xy+y^2=1\\x-y-xy=3\end{matrix}\right.\)

\(\Leftrightarrow\left\{{}\begin{matrix}\left(x-y\right)^2+3xy=1\\x-y-xy=3\end{matrix}\right.\)

Đặt \(\left\{{}\begin{matrix}x-y=u\\xy=v\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}u^2+3v=1\\u-v=3\end{matrix}\right.\)

\(\Rightarrow u^2+3\left(u-3\right)=1\)

\(\Leftrightarrow u^2+3u-10=0\Rightarrow\left[{}\begin{matrix}u=2\Rightarrow v=-1\\u=-5\Rightarrow v=-8\end{matrix}\right.\)

TH1: \(\left\{{}\begin{matrix}u=2\\v=-1\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}x-y=2\\xy=-1\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}y=x-2\\xy=-1\end{matrix}\right.\)

\(\Rightarrow x\left(x-2\right)=-1\Leftrightarrow\left(x-1\right)^2=0\Rightarrow x=1\Rightarrow y=-1\)

TH2: \(\left\{{}\begin{matrix}u=-5\\v=-8\end{matrix}\right.\) \(\Rightarrow...\) bạn tự làm tương tự

a, \(x^2\)≥1

\(\Leftrightarrow\) x>1

b, \(x^2\)<1

\(\Rightarrow\) x∈∅

c, \(x^2\)+3x ≥ 0

\(\Leftrightarrow\) \(x^2\)≥-3x

\(\Leftrightarrow\) x≥-3

d, \(x^2\)+3x+3≥0

\(\Leftrightarrow\) \(\left(x+\dfrac{3}{2}\right)^2\)+\(\dfrac{3}{4}\)≥0+\(\dfrac{3}{4}\)

\(\Leftrightarrow\) \(x^2\)+\(\dfrac{3}{2}^2\)≥0

\(\Leftrightarrow\)\(x^2\)≥\(\dfrac{9}{4}\)

\(\Leftrightarrow\)x≥\(\dfrac{3}{2}\)

\(\left\{{}\begin{matrix}x+y=1\\2x-y=8\end{matrix}\right.\)

\(\Leftrightarrow\left\{{}\begin{matrix}2x+2y=2\\2x-y=8\end{matrix}\right.\)

\(\Leftrightarrow\left\{{}\begin{matrix}x+y=1\\\left(2x-2x\right)+\left(2y+y\right)=2-8\end{matrix}\right.\)

\(\Leftrightarrow\left\{{}\begin{matrix}x+y=1\\3y=-6\end{matrix}\right.\)

\(\Leftrightarrow\left\{{}\begin{matrix}x+y=1\\y=-2\end{matrix}\right.\)

\(\Leftrightarrow\left\{{}\begin{matrix}x-2=1\\y=-2\end{matrix}\right.\)

\(\Leftrightarrow\left\{{}\begin{matrix}x=3\\y=-2\end{matrix}\right.\)

Vậy hệ pt có nghiệm duy nhất \(\left(x;y\right)=\left(3;-2\right)\)

Đáp án D

Cách 1

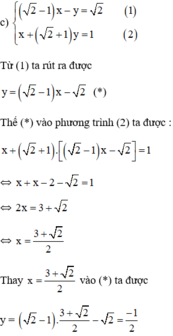
Vậy hệ phương trình có nghiệm duy nhất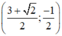 

Cách 2