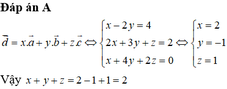Ta có: \(\widehat{ACz}\) và \(\widehat{CAx}\) là hai góc trong cùng phía nên:

           \(\widehat{ACz}\) + \(\widehat{CAx}\) = 180⁰  ⇒ \(\widehat{ACz}\) = 180⁰ - 145⁰ = 35⁰

Mặt khác ta cũng có: \(\widehat{BCz}\) và \(\widehat{CBy}\) là hai góc trong cùng phía nên:

            \(\widehat{BCz}\) + \(\widehat{CBy}\) = 180⁰ ⇒ \(\widehat{BCz}\) = 180⁰ - 120⁰ = 60⁰

\(\widehat{ACB}\) = \(\widehat{ACz}\) + \(\widehat{BCz}\) = 35⁰ + 60⁰ = 95⁰

Kết luận: \(\widehat{ACB}\) = 95⁰

a) Ta có: \(\dfrac{x}{y}=\dfrac{7}{20}\Rightarrow\dfrac{x}{7}=\dfrac{y}{20}\)

\(\dfrac{y}{z}=\dfrac{5}{8}\Rightarrow\dfrac{y}{5}=\dfrac{z}{8}\Rightarrow\dfrac{y}{20}=\dfrac{z}{32}\)

\(\Rightarrow\dfrac{x}{7}=\dfrac{y}{20}=\dfrac{z}{32}\)

\(\Rightarrow\dfrac{2x}{14}=\dfrac{5y}{100}=\dfrac{2z}{64}\)

Áp dụng tc dãy tỉ số bằng nhau:

\(\dfrac{2x}{14}=\dfrac{5y}{100}=\dfrac{2z}{64}=\dfrac{2x+5y-2z}{14+100-64}=2\)

Do \(\left\{{}\begin{matrix}\dfrac{2x}{14}=2\\\dfrac{5y}{100}=2\\\dfrac{2z}{64}=2\end{matrix}\right.\Rightarrow\left\{{}\begin{matrix}x=14\\y=40\\z=64\end{matrix}\right.\).

b) \(5x=8y=20z\Rightarrow\dfrac{5x}{40}=\dfrac{8y}{40}=\dfrac{20z}{40}\)

\(\Rightarrow\dfrac{x}{8}=\dfrac{y}{5}=\dfrac{z}{2}\)

Áp dụng...

\(\dfrac{x}{8}=\dfrac{y}{5}=\dfrac{z}{2}=\dfrac{x-y-z}{8-5-2}=3\)

....

c) \(\dfrac{6}{11}x=\dfrac{9}{2}y=\dfrac{18}{5}z\Rightarrow\dfrac{x}{\dfrac{11}{6}}=\dfrac{y}{\dfrac{2}{9}}=\dfrac{z}{\dfrac{5}{18}}\)

...

ai trả lời hộ với .

Vì xÔy và yÔz là hai góc kề bù :

xÔy + yÔz = 180 độ

Thay xÔy = 120 độ

120 độ + yOz = 180 độ

yOz = 180 độ - 120 độ

yOz = 60 độ

Vì tia Om là tia phân giác của yOz nên :
yOm = mOz = yOz : 2 = 30 độ

Trên cùng một nửa mặt phẳng bờ chứa tia Ox , ta có :

mOz < xOz (vì 30 độ < 180 độ) nên :

Tia Om nằm giữa hai tia Ox và Oz . Ta có:

mOz + xOm = xOz

Thay mOz = 30 độ ; xOz = 180 độ

30 độ + xOm = 180 độ

xOm = 180 độ - 30 độ

xOm = 150 độ

Vì xÔy và yÔz kề bù nhau, nên: + Tia Oy là tia nằm giữa 2 tia Oz và Ox.

+ xÔz = 180^o

^{⇒ xÔy + yÔz = xÔz}

⇒ yÔz = xÔz - xÔy Hay: yÔz = 180⁰ - 120⁰

⇒ yÔz = 60⁰

^{Vì tia Om là tia phân giác của yÔz, nên:}

xÔm = 60⁰ : 2

xÔm = 30⁰

a) Vì x,y,z>0 nên a,b,c>0 (1)

Ta có: a+b-c=x+y+y+z-z-x=2y>0

=> a+b>c. Tương tự ta có b+c>a, c+a>b  (2)

Từ (1) và (2) => Tồn tại tam giác mà các cạnh của nó có độ dài 3 cạnh là a,b,c

b) Vì a,b,c là độ dài 3 cạnh của 1 tam giác nên ta có a+b>c hay x+y+y+z>z+x   =>  y>0

Tương tự: z,x>0

Vậy có các số dương x,y,z tm

Kẻ Bz//Ax//Cy

\(\Rightarrow\widehat{ABC}=\widehat{ABz}+\widehat{zBC}\\ =\left(180^0-\widehat{xAB}\right)+\left(180^0-\widehat{yCB}\right)\left(trong.cùng.phía\right)\\ =50^0+32^0=82^0\)

Trên cùng một nửa mặt phẳng bờ là tia Ox,

Ta có : \(\widehat{xOt}>\widehat{xOz}\) \(\left(120^o>45^o\right)\)

\(\Rightarrow\) Tia Oz nằm giữa 2 tia Ox và Ot

\(\Rightarrow\widehat{xOt}=\widehat{xOz}+\widehat{zOt}\)

\(\Rightarrow120^o=45^o+\widehat{zOt}\)

\(\Rightarrow\widehat{zOt}=120^o-45^o=75^o\) (1)

Ta có : \(\widehat{xOz}>\widehat{xOy}\) \(\left(45^o>30^o\right)\)

\(\Rightarrow\) Tia Oy nằm giữa 2 tia Ox và Oz

\(\Rightarrow\widehat{xOz}=\widehat{xOy}+\widehat{zOy}\)

\(\Rightarrow45^o=30^o+\widehat{zOy}\)

\(\Rightarrow\widehat{zOy}=45^o-30^o=15^o\) (2)

Từ (1) và (2), ta có :

\(\widehat{zOt}-\widehat{zOy}=75^o-15^o=60^o\)

Vậy \(\widehat{zOt}-\widehat{zOy}=60^o\)

Bài 1 : x/3 = y/4 = z/5 => x²/9 = y²/16 = z²/25 
=> 2x²/18 = 2y²/32 = 3z²/75 
=> x²/9 = (2x² + 2y² - 3z²)/(18 + 32 - 75) = - 100/(-25) = 1/4 
=> x²/9 = 1/4 => x² = 9/4 => x = ±3/2 
y²/16 = 1/4 => y² = 4 => y = ± 2 
z²/25 = 1/4 => z² = 25/4 => z = ±5/2 
Mà x, y, z cùng dấu. 
Vậy (x ; y ; z) = (3/2 ; 2 ; 5/2) , (-3/2 ; -2 ; -5/2)

B3 ko tìm được x,y,z thỏa mãn do kết quả là 1 số không dương

Dễ:C

Vì a:b:c=2:3:4

=> Đặt a=2t, b=3t, c=4t 

Gọi diện tích tam giác đó là S.

Ta có: \(S=\dfrac{a.x}{2}=\dfrac{b.y}{2}=\dfrac{c.z}{2}\)

<=> \(2S=ax=by=cz\)

<=>2t.x=3t.y=4t.z

<=>2x=3y=4z

<=>\(\dfrac{x}{6}=\dfrac{y}{4}=\dfrac{z}{3}\)

Vậy..