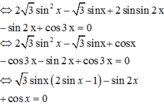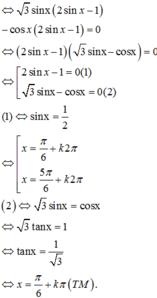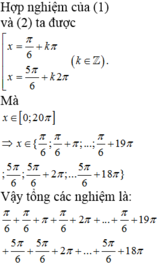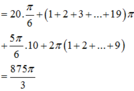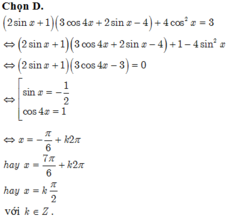(2sinx-1)(2cos2x+2sinx+1)=3-4cos2x

Những câu hỏi liên quan
(2sinx +1)(3cos4x +2sinx -4)+4cos2x=3
\(6sinx.cos4x+4sin^2x-8sinx+3cos4x+2sinx-4+4cos^2x=3\)
\(\Leftrightarrow6sinx.cos4x-6sinx+3cos4x-3=0\)
\(\Leftrightarrow cos4x\left(2sinx+1\right)-\left(2sinx+1\right)=0\)
\(\Leftrightarrow\left(cos4x-1\right)\left(2sinx+1\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}cos4x=1\\sinx=-\dfrac{1}{2}\end{matrix}\right.\)
Đúng 0
Bình luận (0)
(2sinx-1)(2cos2x+2sinx+3)=4sin2x-1
A = (2cosx - 1)(2cos2x + 2sinx +3) +sin2x - 3
Cho phương trình
2
sin
x
-
1
3
tan
x
+
2
sin
x
3
-
4
cos
2
x
Tổng tất cả các nghiệm thuộc đoạn
0
;...
Đọc tiếp
Cho phương trình 2 sin x - 1 3 tan x + 2 sin x = 3 - 4 cos 2 x Tổng tất cả các nghiệm thuộc đoạn 0 ; 20 π của phương trình bằng
A. 1150 3 π
B. 570 3 π
C. 880 3 π
D. 875 3 π
Cho phương trình
2
sin
x
-
1
3
tan
x
+
2
sin
x
3
-
4
cos
2
x
. Tổng tất cả các nghiệm thuộc đoạn
0
;...
Đọc tiếp
Cho phương trình 2 sin x - 1 3 tan x + 2 sin x = 3 - 4 cos 2 x . Tổng tất cả các nghiệm thuộc đoạn 0 ; 20 π của phương trình bằng
A. 1150 3 π
B. 570 3 π
C. 880 3 π
D. 875 3 π
Chọn D.
Phương pháp:
- Sử dụng các công thức nhân ba, phân tích tích thành tổng để biến đổi đơn giản phương trình.
- Giải phương trình, tìm nghiệm thỏa mãn bài toán và tính tổng các nghiệm.
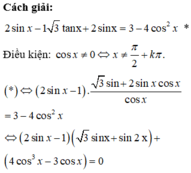
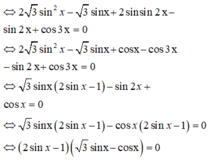
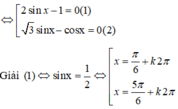

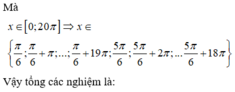
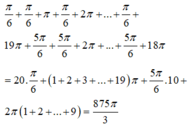
Đúng 0
Bình luận (0)
Cho phương trình
2
sin
x
+
1
3
cos
4
x
+
2
sin
x
-
4
+
4
cos
2...
Đọc tiếp
Cho phương trình 2 sin x + 1 3 cos 4 x + 2 sin x - 4 + 4 cos 2 x = 3 .Số điểm biểu diễn nghiệm của phương trình trên đường tròn lượng giác là:
A.3
B.4
C.5
D.6
Sô nghiệm chung của hai phương trình
4
cos
2
x
-
3
0
và 2sinx+10 trên khoảng
-
π
2
;
3
π
2
là: A. 4. B. 1. C. 2. D. 3.
Đọc tiếp
Sô nghiệm chung của hai phương trình 4 cos 2 x - 3 = 0 và 2sinx+1=0 trên khoảng - π 2 ; 3 π 2 là:
A. 4.
B. 1.
C. 2.
D. 3.
Đáp án C
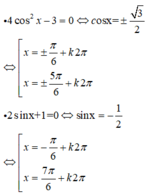
Vậy 2 pt trên có 2 họ nghiệm chung là:
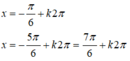
Đúng 0
Bình luận (0)
Số nghiệm chung của hai phương trình
4
cos
2
x
-
3
0
và
2
sin
x
+
1
0
trên khoảng
-
π
2
;
3
π
2
bằng: A. 2 B. 4 C. 3 D. 1
Đọc tiếp
Số nghiệm chung của hai phương trình 4 cos 2 x - 3 = 0 và 2 sin x + 1 = 0 trên khoảng - π 2 ; 3 π 2 bằng:
A. 2
B. 4
C. 3
D. 1
Số nghiệm chung của hai phương trình:
4
cos
2
x
-
3
0
và
2
sin
x
+
1
0
trên khoảng
-
π
2
;
3
π...
Đọc tiếp
Số nghiệm chung của hai phương trình: 4 cos 2 x - 3 = 0 và 2 sin x + 1 = 0 trên khoảng - π 2 ; 3 π 2 bằng:
![]()
![]()
![]()
![]()