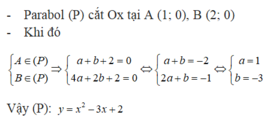Cho Parabol (P): y=x^2 và hai điểm A, B thuộc (P) có hoành độ lần lượt là -1;2. Hãy tìm điểm M trên (P), thuộc cung AB saoo cho tam giác AMB có diện tích lớn nhất. Chứng tỏ rằng tiếp tuyến tại điểm M với (P) song song với đường thẳng AB

Những câu hỏi liên quan
Cho parabol (P): y =\(\dfrac{1}{2}x^2\)
a) Hai điểm A,B thuộc (P) có hoành độ lần lượt là 2;-1. Tìm tọa độ điểm A,B.
b) Viết phương trình đường thẳng đi qua hai điểm A và B
a, - Thay tọa độ hai điểm xA, xB vào (P) ta được : \(\left\{{}\begin{matrix}y_A=2\\y_B=\dfrac{1}{2}\end{matrix}\right.\)
=> Tọa độ 2 điểm A, B lần lượt là : \(\left(2;2\right),\left(-1;\dfrac{1}{2}\right)\) .
b, - Gọi phương trình đường thẳng AB có dạng : y = ax + b .
- Thay tọa độ A, B vào phương trình ta được hệ : \(\left\{{}\begin{matrix}2a+b=2\\-a+b=\dfrac{1}{2}\end{matrix}\right.\)
\(\Rightarrow\left\{{}\begin{matrix}a=\dfrac{1}{2}\\b=1\end{matrix}\right.\)
- Thay lại a, b vào phương trình ta được : \(y=\dfrac{1}{2}x+1\)
Vậy ...
Đúng 2
Bình luận (0)
Cho parabol (P): y a
x
2
+ bx + 2 biết rằng parabol đó cắt trục hoành tại hai điểm lần lượt có hoành độ
x
1
1 và
x
2
2
x
2
2. Parabol đó là: A. y 12
x
2
+ x + 2. B. y −
x
2
+ 2x + 2. C. y 2...
Đọc tiếp
Cho parabol (P): y = a x 2 + bx + 2 biết rằng parabol đó cắt trục hoành tại hai điểm lần lượt có hoành độ x 1 = 1 và x 2 = 2 x 2 = 2. Parabol đó là:
A. y = 12 x 2 + x + 2.
B. y = − x 2 + 2x + 2.
C. y = 2 x 2 + x + 2.
D. y = x 2 −3x + 2.
Cho parabol (P) : \(y=\frac{1}{2}x^2\)và hai điểm A, B thuộc (P) có hoành độ lần lượt là -1 ; 2
Đường thẳng (d) có phượng trình y = mx + n
a) Tìm tọa độ 2 điểm A, B . Tìm m, n biết (d) đi qua 2 điểm A và B
b) Tính độ dài đường cao OH của tam giácOAB.( điểm O là gốc tọa độ )
Cho parabol (P) \(y=\dfrac{1}{2}x^2\) và điểm A, B thuộc (P) có hoành độ lần lượt là: -1, 2. Đường thẳng (d) phương trình y=mx+n
a) Tìm tọa độ điểm A, B. Tìm m, n biết (d) đi qua A và B.
b) Tính độ dài đường cao OH của tam giác OAB (điểm O là gốc tọa độ)
a: F(-1)=1/2(-1)^2=1/2
=>A(-1;1/2)
f(2)=1/2*2^2=2
=>B(2;2)
Theo đề, ta có hệ:
-m+n=1/2 và 2m+n=2
=>m=1/2 và n=1
b: O(0;0); A(-1;0,5); B(2;2)
\(OA=\sqrt{\left(-1-0\right)^2+0,5^2}=\dfrac{\sqrt{5}}{2}\)
\(OB=\sqrt{2^2+2^2}=2\sqrt{2}\)
\(AB=\sqrt{\left(2+1\right)^2+\left(2-0,5\right)^2}=\dfrac{3}{2}\sqrt{5}\)
\(cosO=\dfrac{OA^2+OB^2-AB^2}{2\cdot OA\cdot OB}=\dfrac{-1}{\sqrt{10}}\)
=>\(sinO=\dfrac{3}{\sqrt{10}}\)
\(S_{OAB}=\dfrac{1}{2}\cdot\dfrac{\sqrt{5}}{2}\cdot2\sqrt{2}\cdot\dfrac{3}{\sqrt{10}}=\dfrac{3}{2}\)
=>\(OH=\dfrac{2\cdot\dfrac{3}{2}}{\dfrac{3}{2}\sqrt{5}}=\dfrac{2\sqrt{5}}{5}\)
Đúng 0
Bình luận (0)
Trong mặt phẳng tọa độ Oxy cho parabol (P) có phương trình
y
1
2
x
2
và hai điểm A, B thuộc (P) có hoành độ lần lượt là
x
A
−
1
;
x
B
2
.a) Tìm tọa độ của hai điểm A, B.b) Viết phương trình đường thẳng (d) đi qua hai điểm A, B.c) Tính khoảng cách từ O (gốc tọa độ) đến đường thẳng (d).
Đọc tiếp
Trong mặt phẳng tọa độ Oxy cho parabol (P) có phương trình y = 1 2 x 2 và hai điểm A, B thuộc (P) có hoành độ lần lượt là x A = − 1 ; x B = 2 .
a) Tìm tọa độ của hai điểm A, B.
b) Viết phương trình đường thẳng (d) đi qua hai điểm A, B.
c) Tính khoảng cách từ O (gốc tọa độ) đến đường thẳng (d).
a) Vì A, B thuộc (P) nên:
x A = − 1 ⇒ y A = 1 2 ⋅ - 1 2 = 1 2 x B = 2 ⇒ y B = 1 2 ⋅ 2 2 = 2 ⇒ A − 1 ; 1 2 , B ( 2 ; 2 )
b) Gọi phương trình đường thẳng (d) là y = ax + b.
Ta có hệ phương trình:
− a + b = 1 2 2 a + b = 2 ⇔ 3 a = 3 2 2 a + b = 2 ⇔ a = 1 2 b = 1
Vậy (d): y = 1 2 x + 1 .
c) (d) cắt trục Oy tại điểm C(0; 1) và cắt trục Ox tại điểm D(– 2; 0)
=> OC = 1 và OD = 2
Gọi h là khoảng cách từ O tới (d).
Áp dụng hệ thức về cạnh và đường cao vào ∆ vuông OCD, ta có:
1 h 2 = 1 O C 2 + 1 O D 2 = 1 1 2 + 1 2 2 = 5 4 ⇒ h = 2 5 5
Vậy khoảng cách từ gốc O tới (d) là 2 5 5 .
Đúng 0
Bình luận (0)
Cho hai hàm số y=-x+2 và y=x^2 có đồ thị lần lượt là (d) và (P).
Điểm A thuộc (P) có hoành độ –2; điểm B(0; –1), tìm điểm C thuộc trục hoành sao cho diện tích tam giác ABC bằng 4(đvdt).
a) Vẽ parabol (P) :y =\(2x^2\)
b) Viết phương trình đường thẳng (d) cắt parabol (P) tại hai điểm A và B có hoành độ lần lượt là -1 và 2
a) Ta có bảng giá trị tương ứng x và y sau :
| x | -3 | -2 | -1 | 0 | 1 | 2 | 3 |
| y = 2x2 | 18 | 8 | 2 | 0 | 2 | 8 | 18 |

Quả parabol hơi xấu tí thông cảm =))
2) Cho hàm số 2 y=x2 có đồ thị là parabol (P), hàm số y=(m- 2)x- m+3 có đồ thị là đường thẳng (d).a) Tìm giá trị của m để đường thẳng (d) cắt parabol (P) tại hai điểm phân biệt.b) Gọi A và B là hai giao điểm của (d) và (P), có hoành độ lần lượt là x1 ; x2 . Tìm các giá trị của m để x1,x2 là độ dài hai cạnh của một tam giác vuông cân.
a, - Xét phương trình hoành độ giao điểm :\(x^2=\left(m-2\right)x-m+3\)
\(\Leftrightarrow x^2-\left(m-2\right)x+m-3=0\left(I\right)\)
Có \(\Delta=b^2-4ac=\left(m-2\right)^2-4\left(m-3\right)\)
\(=m^2-4m+4-4m+12=m^2-8m+16=\left(m-4\right)^2\)
- Để P cắt d tại 2 điểm phân biệt <=> PT ( I ) có 2 nghiệm phân biệt .
<=> \(\Delta>0\)
\(\Leftrightarrow\left(m-4\right)^2>0\)
\(\Leftrightarrow m\ne4\)
Vậy ...
b, Hình như đề thiếu giá trị của cạnh huỳnh hay sao á :vvvv
Đúng 2
Bình luận (0)
a) Phương trình hoành độ giao điểm là:
\(x^2=\left(m-2\right)x-m+3\)
\(\Leftrightarrow x^2-\left(m-2\right)x+m-3=0\)
\(\Delta=\left(m-2\right)^2-4\cdot\left(m-3\right)=m^2-4m+4-4m+12=m^2-8m+16\)
Để (d) cắt (P) tại hai điểm phân biệt thì \(\Delta>0\)
\(\Leftrightarrow m^2-8m+16>0\)
\(\Leftrightarrow\left(m-4\right)^2>0\)
mà \(\left(m-4\right)^2\ge0\forall m\)
nên \(m-4\ne0\)
hay \(m\ne4\)
Vậy: khi \(m\ne4\) thì (d) cắt (P) tại hai điểm phân biệt
Đúng 1
Bình luận (0)
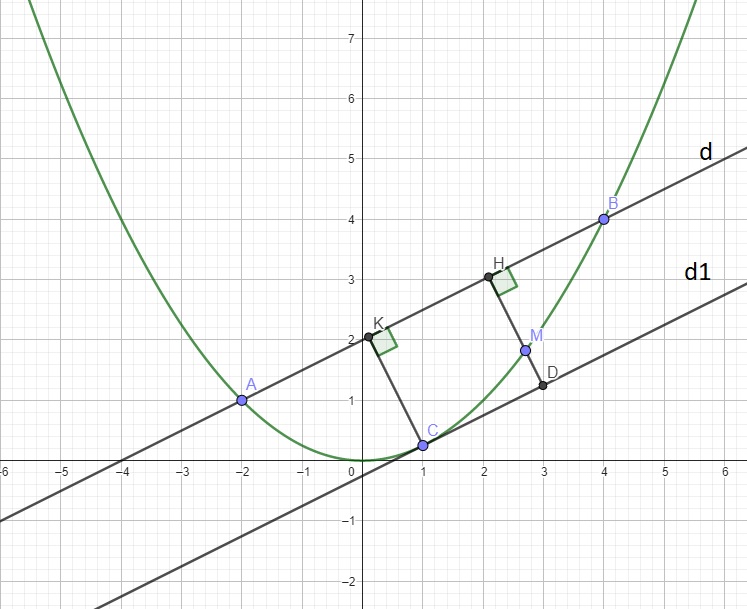
Cho parabol (P): ydfrac{1}{4}x^2 và đường thẳng (d) đi qua 2 điểm A, B trên (P) có hoành độ lần lượt là -2, 4.a. Vẽ (P).b. Viết phương trình đường thẳng (d).c. Tìm tọa độ giao điểm M trên cung AB của (P) có hoành độ xinleft[-2;4right] sao cho tam giác ABC có diện tích lớn nhất.(Thầy NVL giúp em với ạ em cảm ơn thầy nhiều ạ)
Đọc tiếp
Cho parabol (P): \(y=\dfrac{1}{4}x^2\) và đường thẳng (d) đi qua 2 điểm A, B trên (P) có hoành độ lần lượt là \(-2,\) 4.
a. Vẽ (P).
b. Viết phương trình đường thẳng (d).
c. Tìm tọa độ giao điểm M trên cung AB của (P) có hoành độ \(x\in\left[-2;4\right]\) sao cho tam giác ABC có diện tích lớn nhất.
(Thầy NVL giúp em với ạ em cảm ơn thầy nhiều ạ)
a. Em tự giải
b. Từ giả thiết ta có \(A\left(-2;1\right)\) và \(B\left(4;4\right)\)
Gọi phương trình (d) có dạng \(y=ax+b\), do (d) qua A và B nên:
\(\left\{{}\begin{matrix}-2a+b=1\\4a+b=4\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}a=\dfrac{1}{2}\\b=2\end{matrix}\right.\) \(\Rightarrow y=\dfrac{1}{2}x+2\)
c. Câu này có vài cách giải cho lớp 9, cách nhanh nhất là sử dụng tính chất tiếp tuyến.
Từ M kẻ \(MH\perp AB\Rightarrow S_{ABM}=\dfrac{1}{2}MH.AB\)
Do AB cố định \(\Rightarrow S_{max}\) khi \(MH_{max}\)
Gọi \(d_1\) là đường thẳng song song d và tiếp xúc (P), gọi C là tiếp điểm \(d_1\) và (P)
Do \(d_1\) song song (d) nên pt có dạng: \(y=\dfrac{1}{2}x+b\)
Phương trình hoành độ giao điểm \(d_1\) và (P):
\(\dfrac{1}{4}x^2=\dfrac{1}{2}x+b\Rightarrow x^2-2x-4b=0\) (1)
Do \(d_1\) tiếp xúc (P) \(\Rightarrow\left(1\right)\) có nghiệm kép
\(\Rightarrow\Delta'=1+4b=0\Rightarrow b=-\dfrac{1}{4}\)
Thế vào (1) \(\Rightarrow x_C^2-2x_C+1=0\Rightarrow x_C=1\Rightarrow y_C=\dfrac{1}{4}\) \(\Rightarrow C\left(1;\dfrac{1}{4}\right)\)
Từ C kẻ \(CK\perp d\)
Giả sử HM kéo dài cắt \(d_1\) tại D \(\Rightarrow\) tứ giác CKHD là hình chữ nhật (2 cặp cạnh đối song song và 1 góc vuông)
\(\Rightarrow CK=DH\)
Mà \(DH=MH+MD\ge MH\Rightarrow CK\ge MH\)
\(\Rightarrow MH_{max}=CK\) khi M trùng C
Hay \(M\left(1;\dfrac{1}{4}\right)\)
Đúng 3
Bình luận (5)
Ủa câu c là M hay C em nhỉ?
Đúng 0
Bình luận (5)
Cho parabol (P): y x2 và (d): y 2( m-1)x + ma) Tìm m để (d) cắt (P) tại một điểm có hoành độ bằng 2.b) Tìm các giá trị của m để (d) cắt (P) tại hai điểm nằm về hai phía của trục tung có hoành độ lần lượt là x1; x2 sao cho x12 + 2 (m-1)x26
Đọc tiếp
Cho parabol (P): y= x2 và (d): y= 2( m-1)x + m
a) Tìm m để (d) cắt (P) tại một điểm có hoành độ bằng 2.
b) Tìm các giá trị của m để (d) cắt (P) tại hai điểm nằm về hai phía của trục tung có hoành độ lần lượt là x1; x2 sao cho x12 + 2 (m-1)x2=6
a: f(2)=2^2=4
thay x=2 và y=4 vào (d), ta được:
4(m-1)+m=4
=>5m-4=4
=>m=8/5
b: PTHĐGĐ là;
x^2-2(m-1)x-m=0
Để (P) cắt (d) tại hai điểm nằm về hai phía so với trục tung thì -m<0
=>m>0
x1^2+2(m-1)x2=6
=>x1^2+x2(x1+x2)=6
=>x1^2+x2^2+x1x2=6
=>(x1+x2)^2-x1x2=6
=>(2m-2)^2-(-m)-6=0
=>4m^2-8m+4+m-6=0
=>m=2(nhận) hoặc m=-1/4(loại)
Đúng 1
Bình luận (0)