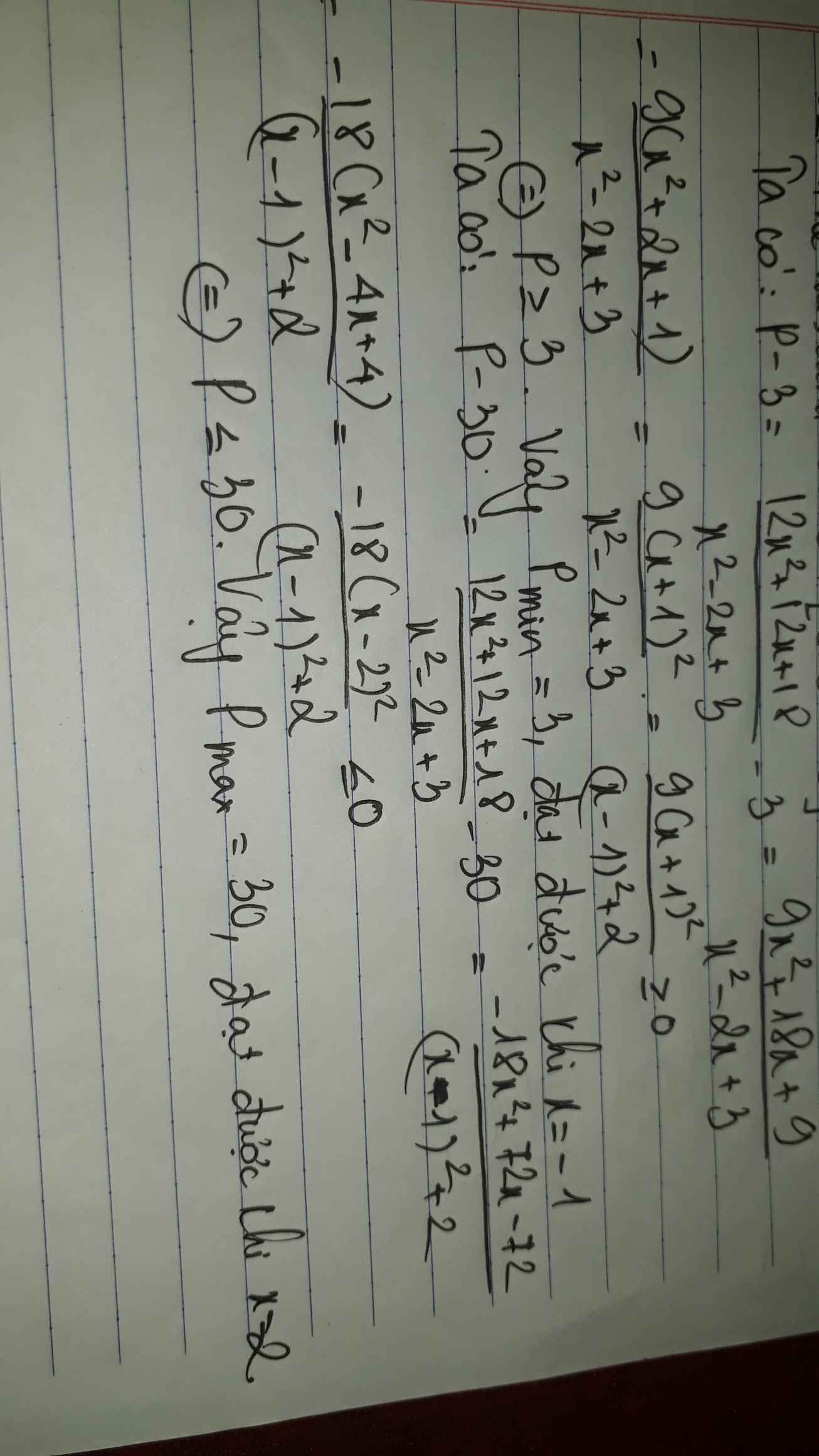Tìm giá trị nhỏ nhất:
A= x^2 - 12x + 18

Những câu hỏi liên quan
tìm giá trị nhỏ nhất:A=|x-2| + |x-20|
Tìm giá trị lớn nhất, nhỏ nhất của biểu thức:
\(P=\dfrac{12x^2+12x+18}{x^2-2x+3}\)
Tìm giá trị nhỏ nhất:a=[x-2021]+[x-2022]
\(a=\left|x-2021\right|+\left|x-2022\right|\)
\(=\left|x-2021\right|+\left|2022-x\right|\)
\(\ge\left|x-2021+2022-x\right|=1\)
\(A=1\Leftrightarrow\left(x-2021\right)\left(2022-x\right)\ge0\)
\(\Rightarrow2021\le x\le2022\)
Đúng 1
Bình luận (1)
tìm giá trị nhỏ nhất:A=x2+2y2-2xy+4x-2y+12
Tìm x để biểu thức sau đạt giá trị nhỏ nhất:
a,A=/x/+5
b,B=/x-2/3/-4
c,C=/3x-1/-1/2
a) Do \(\left|x\right|\ge0\)
\(\Rightarrow A=\left|x\right|+5\ge5\)
\(minA=5\Leftrightarrow x=0\)
b) Do \(\left|x-\dfrac{2}{3}\right|\ge0\)
\(\Rightarrow B=\left|x-\dfrac{2}{3}\right|-4\ge-4\)
\(minB=-4\Leftrightarrow x=\dfrac{2}{3}\)
c) Do \(\left|3x-1\right|\ge0\)
\(\Rightarrow C=\left|3x-1\right|-\dfrac{1}{2}\ge-\dfrac{1}{2}\)
\(minC=-\dfrac{1}{2}\Leftrightarrow x=\dfrac{1}{3}\)
Đúng 2
Bình luận (1)
\(A=\left|x\right|+5\ge5\)
Dấu \("="\Leftrightarrow x=0\)
\(B=\left|x-\dfrac{2}{3}\right|-4\ge-4\)
Dấu \("="\Leftrightarrow x-\dfrac{2}{3}=0\Leftrightarrow x=\dfrac{2}{3}\)
\(C=\left|3x-1\right|-\dfrac{1}{2}\ge-\dfrac{1}{2}\)
Dấu \("="\Leftrightarrow3x-1=0\Leftrightarrow x=\dfrac{1}{3}\)
Đúng 3
Bình luận (1)
Tìm giá trị nhỏ nhất:A=|2x+4|+|y-2|+5
Tìm giá trị nhỏ nhất:a)1,7+|3,4-x| ;b)|x+2,8|-3,5
Tìm giá trị nhỏ nhất:
A= | 2x+1| - |-3/4|
có lời giải chi tiết ạ
A=|2x+1|-3/4>=-3/4
Dấu = xảy ra khi x=-1/2
Đúng 0
Bình luận (0)
Tìm giá trị nhỏ nhất và giá trị lớn nhất của:
A = \(\dfrac{27-12x}{x^2+9}\)
\(A=\dfrac{27-12x}{x^2+9}=\dfrac{x^2-12x+36-\left(x^2+9\right)}{x^2+9}=\dfrac{\left(x-6\right)^2}{x^2+9}-1\ge-1\)
\(A_{min}=-1\Leftrightarrow x=6\)
\(A=\dfrac{27-12x}{x^2+9}=\dfrac{4\left(x^2+9\right)-\left(4x^2+12x+9\right)}{x^2+9}=4-\dfrac{\left(2x+3\right)^2}{x^2+9}\le4\)
\(A_{max}=4\Leftrightarrow x=\dfrac{-3}{2}\)
Đúng 1
Bình luận (0)