Cho a//b. vẽ đường thẳng c cắt đường thẳng a tại điểm H.
Chứng minh rằng: c cũng cắt b
Cho hai đường thẳng phân biệt không song song a và b, điểm M nằm bên trong hai đường thẳng này. Qua M lần lượt vẽ đường thẳng c vuông góc với a tại P, cắt b tại Q và đường thẳng d vuông góc với b tại R, cắt a tại S. Chứng minh rằng đường thẳng qua M, vuông góc với SQ cũng đi qua giao điểm của a và b ?
(a) và (b) không song song nên (a) cắt (b), gọi giao điểm là O. Tam giác OSQ có PQ và RS là hai đường cao gặp nhau tại M nên M là trực tâm của tam giác nên đường thẳng vẽ từ M và vuông góc với SQ là đường cao thứ ba của tam giác tức là đường vuông góc với SQ vẽ từ M cũng đi qua giao điểm của a và b
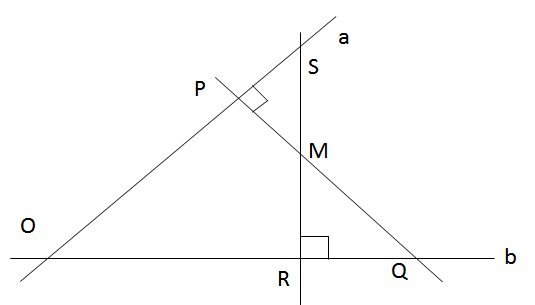
(a) và (b) không song song nên (a) cắt (b), gọi giao điểm là O. Tam giác OSQ có PQ và RS là hai đường cao gặp nhau tại M nên M là trực tâm của tam giác nên đường thẳng vẽ từ M và vuông góc với SQ là đường cao thứ ba của tam giác tức là đường vuông góc với SQ vẽ từ M cũng đi qua giao điểm của a và b
Vì a và b không song song nên chúng cắt nhau giả sử tại A.
Xét ΔAQS có:
QP ⊥ AS (vì QP ⊥ a)
SR ⊥ AQ (vì SR ⊥ b)
Ta có QP và RS cắt nhau tại M. Vậy M là trực tâm của ΔAQS.
=> Đường thẳng đi qua M và vuông góc với QS tại H sẽ là đường cao thứ ba của ΔAQS.
Vậy MH phải đi qua đỉnh A của ΔAQS hay đường thẳng vuông góc với QS đi qua giao điểm của a và b (đpcm).
Cho hai đường thẳng phân biệt không song song a và b, điểm M nằm bên trong hai đường thẳng này. Qua M lần lượt vẽ đường thẳng c vuông góc với a tại P, cắt b tại Q và đường thẳng d vuông góc với b tại R, cắt a tại S. Chứng minh rằng đường thẳng qua M, vuông góc với SQ cũng đi qua giao điểm của a và b.
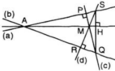
Gọi A là giao điểm của a và b.
Theo giả thiết c ⟘ a hay SR ⟘ AQ hay SR là đường cao của ΔASQ.
d ⟘ b hay PQ ⟘ AS hay QP là đường cao của ΔASQ.
SR cắt QP tại M ⇒ M là trực tâm của ΔASQ
⇒ AM ⟘ SQ
Vậy đường thẳng đi qua M và vuông góc với SQ cũng đi qua A (đpcm).
Cho hai đường thẳng phân biệt không song song a và b, điểm M nằm bên trong hai đường thẳng này. Qua M lần lượt vẽ đường thẳng c vuông góc với a tại P, cắt b tại Q và đường thẳng d vuông góc với b tại R, cắt a tại S. Chứng minh rằng đường thẳng qua M, vuông góc với SQ cũng đi qua giao điểm của a và b.
cho 2 đường thẳng phân biệt không song song;không vuông góc a và b,điểm M không nằm trên 2 đường thẳng này.Qua M lần lượt vẽ đường thẳng c vuông góc với A tại b,cắt b tại Q và đường thẳng d vuông góc với b tại R, cắt a tại S.Chứng minh rằng đường thẳng qua M,vuông góc với SQ cũng đi qua giao điểm của a và b
: Cho AB = 3cm. Đường trung trực của đoạn thẳng AB cắt AB tại M. Kẻ đường thẳng a vuông góc với AB tại A, đường thẳng b vuông góc với AB tại B. Qua điểm E bất kỳ trên đường thẳng a, vẽ đường thẳng song song với AB, đường thẳng đó cắt b tại F.
a) Chứng minh rằng: a // b.
b) Chứng minh rằng: EF FB.
c) Chứng minh rằng: đường thẳng MF cắt đường thẳng a
cho 2 đường thẳng a và b song song . vẽ đường thẳng c đi qua đường thẳng a tại E.chứng minh đường thẳng c cũng cắt đường thẳng b
Trên mặt phẳng có đường thẳng c cắt đường thẳng a tức k song song với a
=> Đường thẳng c cũng không song song với b
Hình như dùng Ơ clit nhưng xl mình quên rồi
Vẽ hai đường thẳng a, b sao cho a // b. Vẽ đường thẳng c cắt a tại điểm A. Hỏi c có cắt b hay không? Hãy suy ra rằng: Nếu a//b và c cắt a thì c cắt b
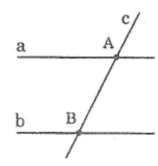
Ta có: a//b, c cắt a tại A
Giả sử c không cắt b thì suy ra c//b
Vậy qua điểm A kẻ được 2 đường thẳng a và c phân biệt cùng song song với b trái với tiên đề Ơ-clit
Vậy a//b, c cắt a thì c cắt b
Cho tam giác ABC. Qua A vẽ đường thẳng a//BC. Qua B vẽ đường thẳng b//AC và qua C vẽ đường thẳng c//AB. Các đường thẳng b và c cắt nhau tại A' và cắt đường thẳng a lần lượt tại C' và B'. Chứng minh rằng: ∆ABC và ∆A'B'C' có cùng một trọng tâm
Cho hai dường tròn (O) và (O) cắt nhau tại A và B. Vẽ các đường kính AOC và AOO'D.Dường thẳng AC cắt đường tròn (O) tại E. Dường thẳng AD cắt đường tròn (O) tại F. Chứng minh rằng: a. Ba điểm C, B, D thẳng hàng. b. Tứ giác CDEF nội tiếp. C. A là tâm đường tròn (hoặc bàng tiếp)của tam giác BEE.
a: góc ABC=1/2*sđ cung AC=90 độ
góc ABD=1/2*180=90 độ
góc CBD=góc ABC+góc ABD=90+90=180 độ
=>C,B,D thẳng hàng
b: góc AFC=1/2*sđ cung AC=90 độ
=>CF vuông góc AD
góc AED=1/2*180=90 độ
=>DE vuông góc AC
góc CED=góc CFD=90 độ
=>CEFD nội tiếp