1, Cho a/b = b/c = c/a
chứng minh : a = b = c
cho :
A= a+b+5 B= b-c-9
C= b-c-4 D= -b-a
Chứng minh A+B = C-D
Ta có :\(\text{VT = A + B}\)
\(\text{= ( a + b + 5 ) + ( b – c – 9 )}\)
\(\text{= a + b + 5 + b – c – 9}\)
\(\text{= a + ( b + b ) – c + ( 5 – 9 )}\)
\(\text{= a + 2b – c – 4 (1)}\)
\(\text{VP = C – D}\)
\(\text{= ( b – c – 4 ) – ( -b – a )}\)
\(\text{= b – c – 4 + b + a}\)
\(\text{= ( b + b ) – c + a – 4}\)
\(\text{= 2b – c + a – 4}\)
\(\text{= a + 2b – c – 4 (2)}\)
\(\text{từ (1) và (2) suy ra}\)\(\text{ A + B = C – D ( đpcm ) }\)
AChứng minh rằng
A=2005^3-1 chia hết cho 2004
B=2005^3+125 chia hết cho 2010
C=x^6+1 chia hết cho (x^2+1)
Mình đang cần gấp
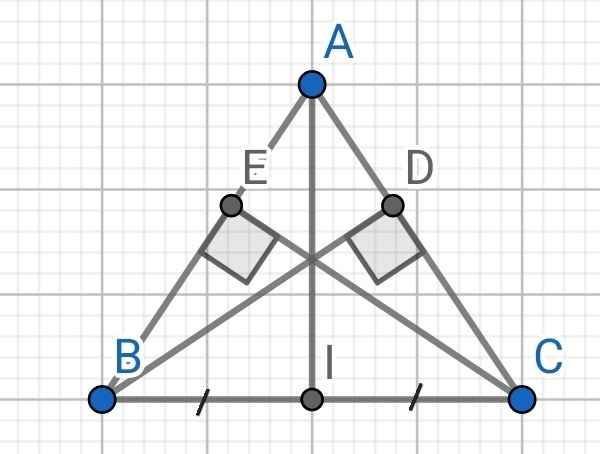
Cho tam giác ABC cân tại A .Từ B kẻ BD vuông góc với AC, CE vuông góc AB.Gọi I là trung điểm cạnh BC
aChứng minh rằng tam giác ABD =tam giác ACE
b Chứng minh AI là tia phân giác của góc BAC
c Chứng minh AI vuông góc vớiBC
Mọi người giúp em ạ mai em thi rồi
 a) Xét hai tam giác vuông: ∆ABD và ∆ACE có:
a) Xét hai tam giác vuông: ∆ABD và ∆ACE có:
AB = AC (do ∆ABC cân tại A)
∠A chung
⇒ ∆ABD = ∆ACE (cạnh huyền - góc nhọn)
b) Do I là trung điểm của BC (gt)
⇒ IB = IC
Xét ∆ABI và ∆ACI có:
AB = AC (cmt)
AI là cạnh chung
BI = CI (cmt)
⇒ ∆ABI = ∆ACI (c-c-c)
⇒ ∠BAI = ∠CAI (hai góc tương ứng)
⇒ AI là tia phân giác của ∠BAC
c) Do ∆ABI = ∆ACI (cmt)
⇒ ∠AIB = ∠AIC (hai góc tương ứng)
Mà ∠AIB + ∠AIC = 180⁰ (kề bù)
⇒ ∠AIB = ∠AIC = 180⁰ : 2 = 90⁰
⇒ AI ⊥ BC
cho tam giác ABC vuông tại A , có góc ABC= 60 độ ,BE là tia phân giác cua góc ABC. Vẽ đường cao EH của tam giác ABC (H thuộc BC)
1 So sánh 3 cạnh cua tam giác ABC
2. aChứng minh AB=HB
b Chứng minh AH vuông góc với BE
3.Chứng minh a .HB=HC
b.AB<EC
1. Xét \(\Delta ABC\) vuông tại A có :
BC > AC ( ch > cgv) ; BC > AB .
2 . a) + b) Xét \(\Delta ABE\) và \(\Delta HBE\) có :
\(\widehat{BAC}=\widehat{EHB}=90^o;BE:chung;\widehat{ABE}=\widehat{HBE}\)
\(\Rightarrow\) \(\Delta ABE\) = \(\Delta HBE\) ( ch- gn)
\(\Rightarrow\) AB = HB
\(\Rightarrow\) \(\Delta ABH\) cân tại B mà BE là phân giác \(\Rightarrow\) BE là đường cao
\(\Rightarrow\) \(BE\perp AH\)
3.a) Xét \(\Delta ABC\) vuông tại A
\(\Rightarrow\) \(\widehat{ABC}+\widehat{BCA}=90^o\Rightarrow\widehat{ACB}=30^o\) ( 1 )
Có BE là phân giác \(\Rightarrow\) \(\widehat{ABE}=\widehat{EBC}=\frac{60^o}{2}=30^o\) (2)
Từ (1) và (2) \(\Rightarrow\) \(\Delta EBC\) cân tại E mà EH là đường cao \(\Rightarrow\) EH là trung tuyến hay BH = CH
b) Xét \(\Delta EHC\) vuông tại H
\(\Rightarrow\) \(EC>HC\left(ch>cgv\right)\)
mà AB = BH ; BH = HC \(\Rightarrow\) \(EC>AB\)
Trên 1 nửa mặt phẳng bờ a, lấy điểm A, trên nửa mặt phẳng đối lấy 2 điểm B,C (A, B, C không thuộc a). Gọi M,N theo thứ tự là giao điểm của AB,AC với đường thẳng aChứng tỏ rằng: Tia BN nằm giữa 2 tia BA, BC Tia CN nằm giữa tia CA, CB
Cho a/b+c + b/c+a + c/a+b = 1. Chứng minh rằng: a/b+c + b/c+a + c/a+b=1. Chứng minh rằng a^2/b+c + b^2/c+a + c^2/a+b
cho a+b+c=2010 và [1/a+b]+[1/b+c]+[1/c+a]=1/3
tính S=[a/b+c]+[b/c+a]+[c/a+b]
giai gium minh minh tick cho
a) Cho a^2 + b^2 + c^2 + 3 = 2(a+b+c). Chứng minh a=b=c=1
b) Cho (a+b+c)^2 = 3(ab+bc+ac). Chứng minh a+b+c
c) Cho (a+b)^2 + (b-c)^2 + (c-a)^2 = (a+b-2c^2) + (b+c-2a^2) + (c+a-2b)^2. Chứng minh a=b=c
Hãy tích cho tui đi
vì câu này dễ mặc dù tui ko biết làm
Yên tâm khi bạn tích cho tui
Tui sẽ ko tích lại bạn đâu
THANKS
\(a^2+b^2+c^2+3\ge2\left(a+b+c\right)\)
\(\Leftrightarrow a^2+b^2+c^2+3-2a-2b-2c\ge0\)
\(\Leftrightarrow\left(a^2-2a+1\right)+\left(b^2-2b+1\right)+\left(c^2-2c+1\right)\ge0\)
\(\Leftrightarrow\left(a-1\right)^2+\left(b-1\right)^2+\left(c-1\right)^2=0\)
Dấu ''='' xảy ra <=> a = b = c = 1
`a^2+b^2+c^2+3=2(a+b+c)`
`<=>a^2+b^2+c^2+3-2a-2b-2c=0`
`<=>a^2-2a+1+b^2-2b+1+c^2-2c+1=0`
`<=>(a-1)^2+(b-1)^2+(c-1)^2=0`
`VT>=0`
Dấu "=" `<=>a=b=c=1`
Áp dụng bđt cosi ta có:
`a^2+b^2>=2ab`
`b^2+c^2>=2bc`
`c^2+a^2>=2ca`
`=>2(a^2+b^2+c^2)>=2(ab+bc+ca)`
`=>a^2+b^2+c^2>=ab+bc+ca`
`=>(a+b+c)^2>=3(ab+bc+ca)`
Dấu '=" `<=>a=b=c`
3 không rõ đề
1)Cho a,b,c >0
Chứng minh bc/a^2(b+c) + ca/b^2(c+a) +ab/c^2(a+b) > hoặc = 1/2(1/a+1/b+1/c)
2) Cho a,b,c>0 1/a + 1/b + 1/c =1
Chứng minh (b+c)/a^2 + (c+a)/b^2 + (a+b)/c^2 > hoặc = 2
1)Cho a,b,c >0
Chứng minh bc/a^2(b+c) + ca/b^2(c+a) +ab/c^2(a+b) > hoặc = 1/2(1/a+1/b+1/c)
2) Cho a,b,c>0 1/a + 1/b + 1/c =1
Chứng minh (b+c)/a^2 + (c+a)/b^2 + (a+b)/c^2 > hoặc = 2
Đọc tiếp...
Cho a, b, c > 0. Chứng minh: (a/b + b/c + c/a)^2 >= (a + b + c)(1/a + 1/b + 1/c)
Giúp minh nhé!!!