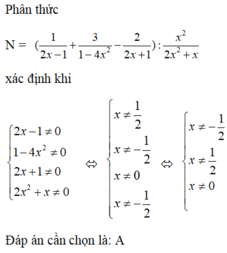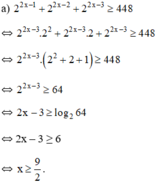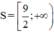22x-1-1=31 => x=

Những câu hỏi liên quan
Cho biểu thức N
(
1
2
x
−
1
+
3
1
−
4
x
2
−
2
2
x
+
1
)
:
x
2...
Đọc tiếp
Cho biểu thức N = ( 1 2 x − 1 + 3 1 − 4 x 2 − 2 2 x + 1 ) : x 2 2 x 2 + x . Rút gọn N ta được
A. N = 2 2 x − 1
B. N = 2 1 - 2 x
C. N = 2 − 2 x − 1
D. N = − 2 1 − 2 x
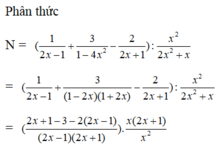
= 2 x + 1 − 3 − 4 x + 2 2 x − 1 2 x + 1 . 2 x + 1 x = − 2 x 2 x − 1 2 x + 1 . 2 x + 1 x = − 2 2 x − 1
Vậy N = 2 1 − 2 x
Đáp án cần chọn là B
Đúng 0
Bình luận (0)
Cho biểu thức N
(
1
2
x
−
1
+
3
1
−
4
x
2
−
2
2
x
+
1
)
:
x
2...
Đọc tiếp
Cho biểu thức N = ( 1 2 x − 1 + 3 1 − 4 x 2 − 2 2 x + 1 ) : x 2 2 x 2 + x . Với giá trị nào của x thì N xác định
A. x ≠ {0; − 1 2 ; 1 2 }
B. x ≠ {-2; 0; 2}
C. x ≠ { − 1 2 ; 1 2 }
D. x ≠ {0; − 1 4 ; 1 4 }
Chứng minh:
a) \(tan(\frac\pi4+\frac{x}2).\frac{1+cos(\frac\pi2+x)}{sin(\frac\pi2+x)}=1\)
b) \(tan(\frac\pi4+x)=\frac{1+sin2x}{cos2x}\)
c) \(\frac{cosx}{1-sinx}=cot(\frac\pi4-\frac{x}{2})\)
d) \(tanx.tan3x=\frac{tan^22x-tan^2x}{1-tan^2x.tan^22x}\)
22x+22x+1+22x+2+...+22x+1918=21923-24
Đặt \(A=2^{2x}+2^{2x+1}+...+2^{2x+1918}\)
=>\(2\cdot A=2^{2x+1}+2^{2x+2}+...+2^{2x+1919}\)
=>\(A=2^{2x+1919}-2^{2x}\)
Theo đề, ta có; \(2^{2x+1919}-2^{2x}=2^{1923}-2^4\)
=>\(2^{2x}\cdot\left(2^{2019}-1\right)=2^4\left(2^{2019}-1\right)\)
=>2x=4
=>x=2
Đúng 0
Bình luận (0)
Bài 1 :
Tìm chữ số tận cùng của số A = 3n+2 - 2n+2 + 3n - 2n
Bài 2:
Chứng minh rằng : nếu (d+2c+4b) chia hết cho 8 thì abcd chia hết cho 8
Bài 3 : Cho C= 2+22 + 23 +......+ 299 + 2100
a) Chứng minh rằng C chia hết cho 31
b) Tìm x để 22x - 2 = C
Bài 3:
a) Ta có: \(C=2+2^2+2^3+...+2^{99}+2^{100}\)
\(=\left(2+2^2+2^3+2^4+2^5\right)+\left(2^6+2^7+2^8+2^9+2^{10}\right)+...+\left(2^{96}+2^{97}+2^{98}+2^{99}+2^{100}\right)\)
\(=2\left(1+2+2^2+2^3+2^4\right)+2^6\left(1+2+2^2+2^3+2^4\right)+...+2^{96}\left(1+2+2^2+2^3+2^4\right)\)
\(=31\cdot\left(2+2^6+...+2^{96}\right)⋮31\)(đpcm)
Đúng 0
Bình luận (0)
Bài 1:
Ta có: \(A=3^{n+2}-2^{n+2}+3^n-2^n\)
\(=3^n\cdot9-2^n\cdot4+3^n-2^n\)
\(=3^n\left(9+1\right)-2^n\left(4+1\right)\)
\(=10\left(3^n-2^{n-1}\right)⋮10\)
Vậy: A có chữ số tận cùng là 0
Bài 2:
Ta có: \(abcd=1000\cdot a+100\cdot b+10\cdot c+d\)
\(\Leftrightarrow abcd=1000\cdot a+96\cdot b+8c+2c+4b+d\)
\(\Leftrightarrow abcd=8\left(125a+12b+c\right)+\left(2c+4b+d\right)\)
mà \(8\left(125a+12b+c\right)⋮8\)
và \(2c+4b+d⋮8\)
nên \(abcd⋮8\)(đpcm)
Đúng 0
Bình luận (0)
Tìm f′(1), f′(2), f′(3) nếu
f
(
x
)
(
x
−
1
)
x
−
2
2
x
−
3
3
Đọc tiếp
Tìm f′(1), f′(2), f′(3) nếu f ( x ) = ( x − 1 ) x − 2 2 x − 3 3
(x-1)^2+(x-2)^2=2(x+4)^2-(22x+27)
\(\left(x-1\right)^2+\left(x-2\right)^2=2\left(x+4\right)^2-\left(22x+27\right)\\ \Rightarrow\left(x^2-2x+1\right)+\left(x^2-4x+4\right)=2\left(x^2+8x+16\right)-\left(22x+27\right)\\ \Rightarrow x^2-2x+1+x^2-4x+4=2x^2+16x+32-22x-27\\ \Rightarrow2x^2-6x+5=2x^2-6x+5\left(luôn.đúng\right)\)
Vậy pt có vô số nghiệm
Đúng 0
Bình luận (0)
Tính nguyên hàm của 1/x^3+x^2-22x-40
\(\int\dfrac{1}{x^3+x^2-22x-40}dx=\int\dfrac{1}{\left(x-5\right)\left(x+2\right)\left(x+4\right)}dx\)
\(=\int\left(\dfrac{1}{63}.\dfrac{1}{x-5}-\dfrac{1}{14}.\dfrac{1}{x+2}+\dfrac{1}{18}.\dfrac{1}{x+4}\right)dx\)
\(=\dfrac{1}{63}ln\left|x-5\right|-\dfrac{1}{14}ln\left|x+2\right|+\dfrac{1}{18}ln\left|x+4\right|+C\)
Đúng 1
Bình luận (0)
Giải các bất phương trình: 2 2 x - 1 + 2 2 x - 2 + 2 2 x - 3 ≥ 448
1/ 4a2-x2-22x-1