Cho tam giác cân tại A,có đường cao AH,BC=7cm.gọiM,N lần lượt là trung điểm AH,AC.tính M,N

Những câu hỏi liên quan
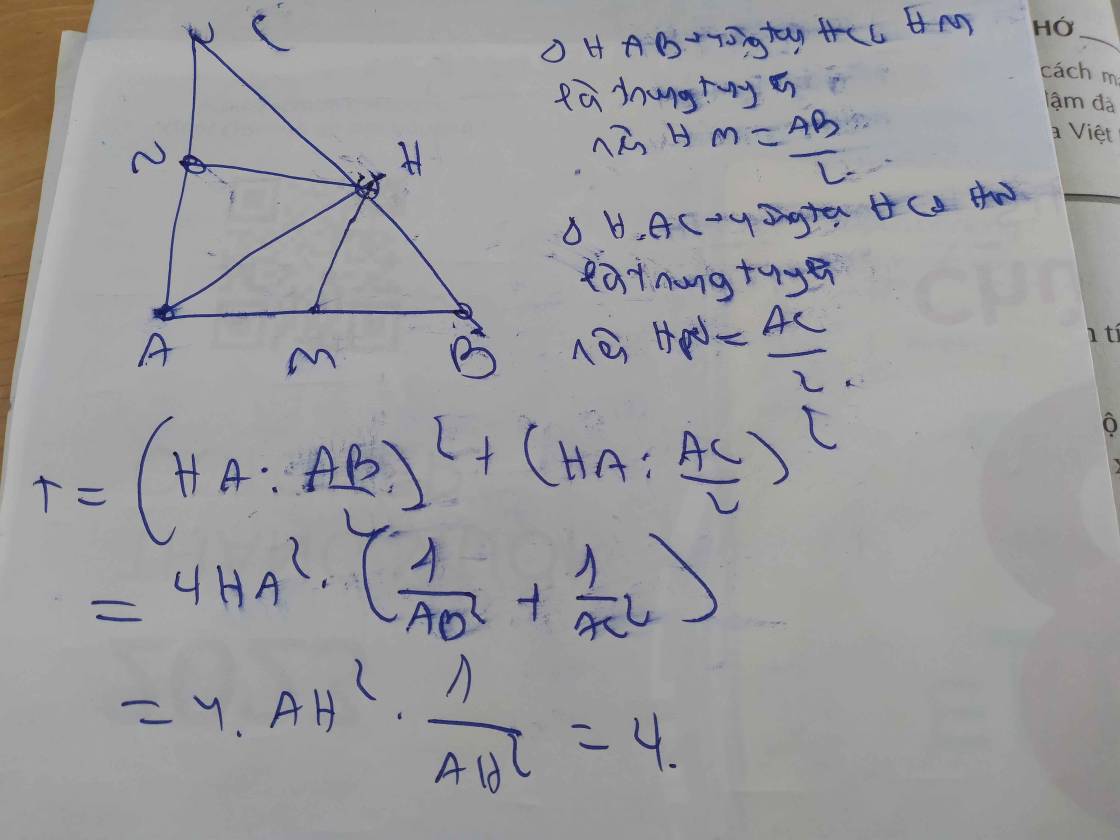
Cho tam giác ABC vuông tại A có đường cao AH. Gọi M, N lần lượt là trung điểm của các cạnh AB, AC.
Tính giá trị của biểu thức: T = (HA/HM)2 + (HA/HN)2
Cho tam giác ABC cân tại A ,có đường cao AH biết cạnh BC bằng 8 cm các điểm M, N, P lần lượt là trung điểm của các cạnh AB, AH,AC, từ B kẻ đường thẳng song song với BC cắt MP tại I.a,Tính độ dài cạnh MPb,tứ giác NIBH là hình gì?c,Tứ giác HCBN là hình gì?d,Tứ giác MPCB là hình gì?e,Tứ giác NAIB là hình gì ?f,Tứ giác AMHP là gì ?g,Lấy K đối xứng với I qua H, Chứng minh rằng CK song song với BI
Xem chi tiết
1) Cho tam giác ABC có ABAC, AH là đường cao. Goi M, N, K lần lượt là trung điểm AB, AC, BCa)Chứng minh MNKH là hình thang cân b)Tia AH và tia AK lần lượt lấy điểm E và D sao cho H là trung điểm AE và K là trung điểm của AD. Chứng minh tứ giác BCDE là hình thang cân 2) Cho tam giác ABC có Â90 độ. Bên ngoài tam giác ABC, vẽ tam giác ABD và tam giác ACE vuông cân tại A a) Chứng minh CDBE b) Gọi M,N,P lần lượt là trung điểm của BD, CE, BC. Chứng minh tam giác MNPlà tam giác vuông cân
Đọc tiếp
1) Cho tam giác ABC có AB<AC, AH là đường cao. Goi M, N, K lần lượt là trung điểm AB, AC, BC
a)Chứng minh MNKH là hình thang cân
b)Tia AH và tia AK lần lượt lấy điểm E và D sao cho H là trung điểm AE và K là trung điểm của AD. Chứng minh tứ giác BCDE là hình thang cân
2) Cho tam giác ABC có Â>90 độ. Bên ngoài tam giác ABC, vẽ tam giác ABD và tam giác ACE vuông cân tại A
a) Chứng minh CD=BE
b) Gọi M,N,P lần lượt là trung điểm của BD, CE, BC. Chứng minh tam giác MNPlà tam giác vuông cân
Bài 1 :
a) Ta có : \(\hept{\begin{cases}AM=MB\\AN=NC\end{cases}\Rightarrow}\)MN là đường trung bình tam giác ABC \(\Rightarrow MN\text{//}BC\) hay \(MN\text{//}HK\left(1\right)\)
Dễ thấy MNKB là hình bình hành => \(\widehat{MNK}=\widehat{ABC}=\widehat{MHB}\)(Vì tam giác AHB vuông có HM là đường trung tuyến ứng với cạnh huyền.) . Mặt khác : \(\widehat{MNK}=\widehat{CKN}\)(hai góc ở vị trí so le trong)
=> \(\widehat{MHB}=\widehat{CKN}\). Mà hai góc này lần lượt bù với \(\widehat{MHK}\)và \(\widehat{HKN}\)=> \(\widehat{MHK}=\widehat{HKN}\) (2)
Từ (1) và (2) suy ra MNKH là hình thang cân.
b) Dễ thấy HK là đường trung bình tam giác AED => HK // ED hay BC // ED (3)
Tương tự , MH và NK lần lượt là các đường trung bình của các tam giác ABE và ACD
=> BE = 2MH ; CD = 2NK mà MH = NK (MNKH là hình thang cân - câu a)
=> BE = CD (4)
Từ (3) và (4) suy ra BCDE là hình thang cân.
Đúng 0
Bình luận (0)
Bài 2 :
a) Ta có : \(\widehat{BAD}=\widehat{CAE}=90^o\Rightarrow\widehat{BAD}+\widehat{DAE}=\widehat{CAE}+\widehat{DAE}\Rightarrow\widehat{BAE}=\widehat{CAD}\)
Xét tam giác BAE và tam giác CAD có : \(AB=AD\left(gt\right)\); \(AC=AE\left(gt\right)\) ; \(\widehat{BAE}=\widehat{CAD}\left(cmt\right)\)
\(\Rightarrow\Delta BAE=\Delta CAD\left(c.g.c\right)\Rightarrow CD=BE\)
b) Dễ dàng chứng minh được MP và PN lần lượt là các đường trung bình của các tam giác ACD và tam giác BEC
=> MP = 1/2CD ; PN = 1/2 BE mà CD = BE => MP = PN => tam giác MNP cân tại P
Để chứng minh góc MPN = 90 độ , hãy chứng minh BE vuông góc với CD.
Đúng 0
Bình luận (0)
Cho tam giác ABC vuông tại A, đường cao AH. M và N lần lượt là hình chiếu của H trên
AB, AC. Gọi E; F lần lượt là trung điểm của AH; HC. Giả sử AC = 2AB thì tam giác BHE vuông cân.
Xét ΔAHB vuông tại H và ΔCHA vuông tại H có
\(\widehat{HAB}=\widehat{HCA}\left(=90^0-\widehat{B}\right)\)
Do đó: ΔAHB đồng dạng với ΔCHA
=>\(\dfrac{HB}{HA}=\dfrac{AB}{CA}=\dfrac{1}{2}\)
=>AH=2HB
mà AH=2HE
nên HE=HB
Xét ΔHEB vuông tại H có HE=HB
nên ΔHEB vuông cân tại H
Đúng 0
Bình luận (0)
Cho tam giác ABC vuông tại A, đường cao AH. M và N lần lượt là hình chiếu của H trên AB, AC. Gọi E; F lần lượt là trung điểm của AH; HC. Giả sử AC = 2AB thì tam giác BHE vuông cân.
Cho tam giác ABC cân tại A có ah là đường cao Gọi M và N lần lượt là trung điểm của hai cạnh AB và AC biết ah 8 cm và BC 4 cm Tính diện tích ABC và độ dài cạnh M N E là điểm đối xứng h qua m ơ Chứng minh tứ giác hbe là hình chữ nhật gọi F là điểm đối xứng a qua h Chứng minh tứ giác AB AC là hình thoi cho biết HK vuông góc FC tại A I là trung điểm HK chứng minh rằng đừng pk vuông góc với EF
Đọc tiếp
Cho tam giác ABC cân tại A có ah là đường cao Gọi M và N lần lượt là trung điểm của hai cạnh AB và AC biết ah = 8 cm và BC = 4 cm Tính diện tích ABC và độ dài cạnh M N E là điểm đối xứng h qua m ơ Chứng minh tứ giác hbe là hình chữ nhật gọi F là điểm đối xứng a qua h Chứng minh tứ giác AB AC là hình thoi cho biết HK vuông góc FC tại A I là trung điểm HK chứng minh rằng đừng pk vuông góc với EF
a: \(S_{ABC}=\dfrac{1}{2}\cdot8\cdot4=16\left(cm^2\right)\)
b: Xét tứ giác AHBE có
M là trung điểm chung của AB và HE
góc AHB=90 độ
=>AHBE là hình chữ nhật
c: Xét tứ giác ABFC có
H là trung điểm chung của AF và BC
AB=AC
=>ABFC là hình thoi
Đúng 0
Bình luận (0)
Cho tam giác ABC có AB=AC=\(\sqrt{5}\) cm,độ dài đường cao AH=\(\sqrt{3}\) cm .Gọi M,N lần lượt là trung điểm của HC và AC.Tính độ dài đoạn thẳng AM và BN
Do AH là đường cao trong tam giác ABC cân tại A nên AH cùng là đường trung tuyến
\(\Rightarrow\)H là trung điểm của BC
Áp dụng định lý py-ta-go vào tam giác vuông AHC có:
\(HC=\sqrt{AC^2-AH^2}=\sqrt{2}\left(cm\right)\)
Do M là trung điểm của HC\(\Rightarrow HM=\dfrac{HC}{2}=\dfrac{\sqrt{2}}{2}\) (cm)
Áp dụng định lý py-ta-go vào tam giác AMH vuông có:
\(AH^2+HM^2=AM^2\)
\(\Leftrightarrow AM=\sqrt{AH^2+HM^2}=\sqrt{3+\dfrac{1}{2}}=\dfrac{\sqrt{14}}{2}\left(cm\right)\)
Có M và H lần lượt là tđ của HC và CA
Suy ra MN là đường trung bình của tam giác AHC
\(\Rightarrow\) MN//AH và \(MN=\dfrac{AH}{2}=\dfrac{\sqrt{3}}{2}\)(cm)
Vì \(AH\perp BC\)\(\Rightarrow MN\perp BC\)
Áp dụng định lý py-ta-go vào tam giác BNM vuông có:
\(BN^2=MN^2+BM^2=\dfrac{3}{4}+\left(BC-MC\right)^2=\dfrac{3}{4}+\left(2HC-HM\right)^2=\dfrac{3}{4}+\dfrac{9}{2}=\dfrac{21}{4}\)
\(\Rightarrow BN=\dfrac{\sqrt{21}}{2}\) (cm)
Vậy...
Đúng 2
Bình luận (1)
\(AB=AC\Rightarrow\Delta ABC\) cân tại A \(\Rightarrow\) AH là đường cao đồng thời là trung tuyến hay H là trung điểm BC
\(\Rightarrow BH=CH\)
Pitago cho tam giác ACH: \(CH=\sqrt{AC^2-AH^2}=\sqrt{2}\)
\(\Rightarrow HM=\dfrac{1}{2}CH=\dfrac{\sqrt{2}}{2}\) \(\Rightarrow BM=BH+HM=CH+HM=\dfrac{3\sqrt{2}}{2}\)
Pitago tam giác AHM: \(AM=\sqrt{AH^2+HM^2}=\dfrac{\sqrt{14}}{2}\)
Do N là trung điểm AC, M là trung điểm HC \(\Rightarrow MN\) là đường trung bình tam giác ACH
\(\Rightarrow\left\{{}\begin{matrix}MN||AH\Rightarrow MN\perp BC\\MN=\dfrac{1}{2}AH=\dfrac{\sqrt{3}}{2}\end{matrix}\right.\)
Pitago tam giác BMN: \(BN=\sqrt{BM^2+MN^2}=\dfrac{\sqrt{21}}{2}\)
Đúng 2
Bình luận (1)
Xem thêm câu trả lời
Cho có tam giác ABC có Ab < AC. Gọi M, N, K lần lượt là trung điểm của AB, AC, BC.
a) Chứng minh BMKN là hình thang
b) Hạ đường cao AH, biết AH cắt MK tại I. Chứng minh tam giác MAH cân tại M.
c) Chứng minh MNKH là hình thang cân.
a: Xét ΔABC có
M là trung điểm của AB
N là trung điểm của AC
Do đó: MN là đường trung bình của ΔBAC
Suy ra: MN//BC
hay MN//BK
Xét tứ giác BMNK có MN//BK
nên BMNK là hình thang
b: Ta có: ΔAHB vuông tại H
mà HM là đường trung tuyến ứng với cạnh huyền AB
nên HM=AM=MB
Xét ΔMAH có MA=MH
nên ΔMAH cân tại M
Đúng 0
Bình luận (0)
3: Cho tam giác ABC vuông tại A, đường cao AH. Đường phân giác trong góc B cắt AH, AC lần lượt tại E và F. Đường phân
giác trong góc C cắt AH, AB lần lượt tại K và L. M và N lần lượt là trung điểm của EF và KL. Chứng minh MN // BC