\(\left(\sqrt{12-\sqrt{27}+\sqrt{3}}\right)\) : \(\sqrt{3}\)
\(\left(5\sqrt{3}+3\sqrt{5}\right):\sqrt{15}\)
\(\sqrt{27\left(1-\sqrt{3}\right)^2}:3\sqrt{15}\)
Những câu hỏi liên quan
Bài 1: Rút gọn biểu thức1) sqrt{12}-sqrt{27}+sqrt{48} 2) left(sqrt{25}+sqrt{20}-sqrt{80}right):sqrt{5}3) 2sqrt{27}-sqrt{frac{16}{3}}-sqrt{48}-sqrt{8frac{1}{3}} 4) frac{1}{sqrt{5}-sqrt{3}}-frac{1}{sqrt{5}+sqrt{3}}5) left(sqrt{125}-sqrt{12}-2sqrt{5}right)left(3sqrt{5}-sqrt{3}+sqrt{27}right) 6) left(3sqrt{20}-sqrt{125}-15sqrt{frac{1}{5}}right).sqrt{5}7) left(6sqrt{128}-frac{3}{5}sqrt{50}+7sqrt{8}right):3sqrt{2} 8) left(2sqrt{48}-frac{3}{2}sqrt{frac{4}{3}}+sqrt{27}right).2sqrt{3...
Đọc tiếp
Bài 1: Rút gọn biểu thức
1) \(\sqrt{12}-\sqrt{27}+\sqrt{48}\) 2) \(\left(\sqrt{25}+\sqrt{20}-\sqrt{80}\right):\sqrt{5}\)
3) \(2\sqrt{27}-\sqrt{\frac{16}{3}}-\sqrt{48}-\sqrt{8\frac{1}{3}}\) 4) \(\frac{1}{\sqrt{5}-\sqrt{3}}-\frac{1}{\sqrt{5}+\sqrt{3}}\)
5) \(\left(\sqrt{125}-\sqrt{12}-2\sqrt{5}\right)\left(3\sqrt{5}-\sqrt{3}+\sqrt{27}\right)\) 6) \(\left(3\sqrt{20}-\sqrt{125}-15\sqrt{\frac{1}{5}}\right).\sqrt{5}\)
7) \(\left(6\sqrt{128}-\frac{3}{5}\sqrt{50}+7\sqrt{8}\right):3\sqrt{2}\) 8) \(\left(2\sqrt{48}-\frac{3}{2}\sqrt{\frac{4}{3}}+\sqrt{27}\right).2\sqrt{3}\)
9) \(\sqrt{\left(3-2\sqrt{2}\right)^2}-\sqrt{\left(\sqrt{8}-4\right)^2}\) 10) \(\sqrt{\left(4-\sqrt{15}\right)^2}+\sqrt{\left(\sqrt{15}-3\right)^2}\)
11) \(\frac{\sqrt{10}-\sqrt{2}}{\sqrt{5}-1}+\frac{2-\sqrt{2}}{\sqrt{2}-1}\) 12) \(\left(1-\frac{5+\sqrt{5}}{1+\sqrt{5}}\right)\left(\frac{5-\sqrt{5}}{1-\sqrt{5}}-1\right)\)
13) \(\sqrt{15-6\sqrt{6}}\) 14) \(\sqrt{8-2\sqrt{15}}\) 15) \(\sqrt[3]{-2}.\sqrt[3]{32}+\sqrt{2}.\sqrt{32}\)
Rút gọn các biểu thức:
1. Aleft(sqrt{5}-2right)left(sqrt{5}+2right)
2. B left(sqrt{45}+sqrt{63}right)left(sqrt{7}-sqrt{5}right)
3. C left(sqrt{5}+sqrt{3}right)left(5-sqrt{15}right)
4. D left(sqrt{32}-sqrt{50}+sqrt{27}right)left(sqrt{27}+sqrt{50}-sqrt{32}right)
5. E left(sqrt{3}+1right)^2-2sqrt{3}+4
6. F left(sqrt{15}-2sqrt{3}right)^2+12sqrt{5}
Đọc tiếp
Rút gọn các biểu thức:
1. A=\(\left(\sqrt{5}-2\right)\left(\sqrt{5}+2\right)\)
2. B= \(\left(\sqrt{45}+\sqrt{63}\right)\left(\sqrt{7}-\sqrt{5}\right)\)
3. C= \(\left(\sqrt{5}+\sqrt{3}\right)\left(5-\sqrt{15}\right)\)
4. D= \(\left(\sqrt{32}-\sqrt{50}+\sqrt{27}\right)\left(\sqrt{27}+\sqrt{50}-\sqrt{32}\right)\)
5. E= \(\left(\sqrt{3}+1\right)^2-2\sqrt{3}+4\)
6. F= \(\left(\sqrt{15}-2\sqrt{3}\right)^2+12\sqrt{5}\)
\(1.A=\left(\sqrt{5}-2\right)\left(\sqrt{5}+2\right)=5-4=1\)
\(2.B=\left(\sqrt{45}+\sqrt{63}\right)\left(\sqrt{7}-\sqrt{5}\right)=\left(3\sqrt{5}+3\sqrt{7}\right)\left(\sqrt{7}-\sqrt{5}\right)=2\left(7-5\right)=4\) \(3.C=\left(\sqrt{5}+\sqrt{3}\right)\left(5-\sqrt{15}\right)=\sqrt{5}\left(\sqrt{5}+\sqrt{3}\right)\left(\sqrt{5}-\sqrt{3}\right)=\sqrt{5}\left(5-3\right)=2\sqrt{5}\) \(4.\left(\sqrt{32}-\sqrt{50}+\sqrt{27}\right)\left(\sqrt{27}+\sqrt{50}-\sqrt{32}\right)=\left(4\sqrt{2}-5\sqrt{2}+3\sqrt{3}\right)\left(3\sqrt{3}+5\sqrt{2}-4\sqrt{2}\right)=\left(3\sqrt{3}-\sqrt{2}\right)\left(3\sqrt{3}+\sqrt{2}\right)=27-2=25\) \(5.E=\left(\sqrt{3}+1\right)^2-2\sqrt{3}+4=4+2\sqrt{3}-2\sqrt{3}+4=8\)
\(6.F=\left(\sqrt{15}-2\sqrt{3}\right)^2+12\sqrt{5}=27-12\sqrt{5}+12\sqrt{5}=27\)
Đúng 0
Bình luận (0)
Tính giá trị các biểu thức:
a.\(\left(7\sqrt{48}+3\sqrt{27}-2\sqrt{12}\right)\sqrt{3}\)
b.\(\left(12\sqrt{50}-8\sqrt{200}+7\sqrt{450}\right):\sqrt{10}\)
c.\(\left(2\sqrt{6}-4\sqrt{3}+5\sqrt{2}-\dfrac{1}{4}\sqrt{8}\right)3\sqrt{6}\)
d.\(3\sqrt{15\sqrt{50}}+5\sqrt{24\sqrt{8}}-4\sqrt{12\sqrt{32}}\)
a) Ta có: \(\left(7\sqrt{48}+3\sqrt{27}-2\sqrt{12}\right)\cdot\sqrt{3}\)
\(=\left(7\cdot4\sqrt{3}+3\cdot3\sqrt{3}-2\cdot2\sqrt{3}\right)\cdot\sqrt{3}\)
\(=33\sqrt{3}\cdot\sqrt{3}\)
=99
b) Ta có: \(\left(12\sqrt{50}-8\sqrt{200}+7\sqrt{450}\right):\sqrt{10}\)
\(=\left(12\cdot5\sqrt{2}-8\cdot10\sqrt{2}+7\cdot15\sqrt{2}\right):\sqrt{10}\)
\(=\dfrac{85\sqrt{2}}{\sqrt{10}}=\dfrac{85}{\sqrt{5}}=17\sqrt{5}\)
c) Ta có: \(\left(2\sqrt{6}-4\sqrt{3}+5\sqrt{2}-\dfrac{1}{4}\sqrt{8}\right)\cdot3\sqrt{6}\)
\(=\left(2\sqrt{6}-4\sqrt{3}+5\sqrt{2}-\dfrac{1}{4}\cdot2\sqrt{2}\right)\cdot3\sqrt{6}\)
\(=\left(2\sqrt{6}-4\sqrt{3}+3\sqrt{2}\right)\cdot3\sqrt{6}\)
\(=36-36\sqrt{2}+18\sqrt{3}\)
d) Ta có: \(3\sqrt{15\sqrt{50}}+5\sqrt{24\sqrt{8}}-4\sqrt{12\sqrt{32}}\)
\(=3\cdot\sqrt{75\sqrt{2}}+5\cdot\sqrt{48\sqrt{2}}-4\sqrt{48\sqrt{2}}\)
\(=3\cdot5\sqrt{2}\cdot\sqrt{\sqrt{2}}+4\sqrt{3}\sqrt{\sqrt{2}}\)
\(=15\sqrt{\sqrt{8}}+4\sqrt{\sqrt{18}}\)
Đúng 3
Bình luận (0)
a,=\(\left(28\sqrt{3}+9\sqrt{3}-4\sqrt{3}\right).\sqrt{3}\)
\(=28.3+9.3-4.3=99\)
b,\(=\left(60\sqrt{2}-80\sqrt{2}+175\sqrt{2}\right):\sqrt{10}\)
\(=155\sqrt{2}:\sqrt{10}=\dfrac{155}{\sqrt{5}}\)
Đúng 1
Bình luận (0)
d,Ta có:\(3\sqrt{15\sqrt{50}}+5\sqrt{24\sqrt{8}}-4\sqrt{12\sqrt{32}}\)
\(=3\sqrt{75\sqrt{2}}+5\sqrt{48\sqrt{2}}-4\sqrt{48\sqrt{2}}\)
\(=15\sqrt{3\sqrt{2}}+20\sqrt{3\sqrt{2}}-16\sqrt{3\sqrt{2}}\)
\(=19\sqrt{3\sqrt{2}}\)
Đúng 1
Bình luận (0)
a) A=\(\left(\dfrac{2+\sqrt{2}}{\sqrt{2}+1}-\dfrac{\sqrt{15}-\sqrt{35}}{\sqrt{3}-\sqrt{7}}\right).\left(\sqrt{2}+\sqrt{5}\right)\)
b) B=\(\dfrac{12}{3+\sqrt{3}}-\dfrac{6}{\sqrt{3}}+\dfrac{\sqrt{27}-3\sqrt{2}}{\sqrt{3}.\sqrt{2}}\)
c)C=\(\left(\dfrac{1}{\sqrt{x}-1}-\dfrac{1}{\sqrt{x}}\right).\left(\dfrac{\sqrt{x}+1}{\sqrt{x}-2}-\dfrac{\sqrt{x}+2}{\sqrt{x}-1}\right)\)(x>0,x≠1,x≠4)
\(A=\left(\dfrac{\sqrt{2}\left(\sqrt{2}+1\right)}{\sqrt{2}+1}-\dfrac{\sqrt{5}\left(\sqrt{3}-\sqrt{7}\right)}{\sqrt{3}-\sqrt{7}}\right).\left(\sqrt{2}+\sqrt{5}\right)\)
\(=\left(\sqrt{2}-\sqrt{5}\right)\left(\sqrt{2}+\sqrt{5}\right)=2-5=-3\)
\(B=\dfrac{12\left(3-\sqrt{3}\right)}{\left(3+\sqrt{3}\right)\left(3-\sqrt{3}\right)}-\dfrac{2\sqrt{3}.\sqrt{3}}{\sqrt{3}}+\dfrac{3}{\sqrt{2}}-\dfrac{3}{\sqrt{3}}\)
\(=\dfrac{12\left(3-\sqrt{3}\right)}{6}-2\sqrt{3}+\dfrac{3\sqrt{2}}{2}-\sqrt{3}\)
\(=2\left(3-\sqrt{3}\right)-3\sqrt{3}+\dfrac{3\sqrt{2}}{2}=6-5\sqrt{3}+\dfrac{3\sqrt{2}}{2}\) (câu này khả năng đề sai, dấu \(\sqrt{3}.\sqrt{2}\) ở mẫu cuối cùng là dấu trừ mới hợp lý)
\(C=\left(\dfrac{\sqrt{x}}{\sqrt{x}\left(\sqrt{x}-1\right)}-\dfrac{\sqrt{x}-1}{\sqrt{x}\left(\sqrt{x}-1\right)}\right).\left(\dfrac{\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}{\left(\sqrt{x}-2\right)\left(\sqrt{x}-1\right)}-\dfrac{\left(\sqrt{x}-2\right)\left(\sqrt{x}+2\right)}{\left(\sqrt{x}-2\right)\left(\sqrt{x}-1\right)}\right)\)
\(=\dfrac{1}{\sqrt{x}\left(\sqrt{x}-1\right)}.\dfrac{3}{\left(\sqrt{x}-2\right)\left(\sqrt{x}-1\right)}=\dfrac{3}{\sqrt{x}\left(\sqrt{x}-2\right)\left(\sqrt{x}-1\right)^2}\)
Dấu giữa 2 dấu ngoặc là dấu chia sẽ hợp lý hơn
Đúng 0
Bình luận (0)
a)\(\left(7\sqrt{48}+3\sqrt{27}-2\sqrt{12}\right):\sqrt{3}\)
b)\(\sqrt{27\left(1-\sqrt{3}\right)^4}:3\sqrt{15}\)
c) \(\frac{\sqrt{6+2\sqrt{5}}}{\sqrt{5}+1}\)
21 tháng 12 2023 lúc 15:18
Bài 1: Tínha) 5sqrt{8}-4sqrt{27}-2sqrt{75}+sqrt{108} b) 1sqrt{left(3-sqrt{6}right)^2}+sqrt{left(1-sqrt{6}right)^2} c) dfrac{5sqrt{3}-3sqrt{5}}{sqrt{5}-sqrt{3}}+dfrac{1}{4+sqrt{15}} d) dfrac{2sqrt{3-sqrt{5}}left(3+sqrt{5}right)}{sqrt{10}-sqrt{2}}-dfrac{sqrt{15}+sqrt{5}}{sqrt{12}+2} Bài 2: Cho (d₁): y dfrac{1}{2}x-4 và (d₂): y -3x+3 . Vẽ (d₁) và (d₂) trên cùng một hệ trục tọa độ. Tìm tọa độ giao điểm A của 2 đường thẳng trên. Helpp!!
Đọc tiếp
Bài 1: Tính
a) \(5\sqrt{8}-4\sqrt{27}-2\sqrt{75}+\sqrt{108}\)
b) \(1\sqrt{\left(3-\sqrt{6}\right)^2}+\sqrt{\left(1-\sqrt{6}\right)^2}\)
c) \(\dfrac{5\sqrt{3}-3\sqrt{5}}{\sqrt{5}-\sqrt{3}}+\dfrac{1}{4+\sqrt{15}}\)
d) \(\dfrac{2\sqrt{3-\sqrt{5}}\left(3+\sqrt{5}\right)}{\sqrt{10}-\sqrt{2}}-\dfrac{\sqrt{15}+\sqrt{5}}{\sqrt{12}+2}\)
Bài 2: Cho (d₁): y = \(\dfrac{1}{2}x-4\) và (d₂): y = \(-3x+3\) . Vẽ (d₁) và (d₂) trên cùng một hệ trục tọa độ. Tìm tọa độ giao điểm A của 2 đường thẳng trên.
Helpp!!
Bài 1:
a: \(5\sqrt{8}-4\sqrt{27}-2\sqrt{75}+\sqrt{108}\)
\(=5\cdot2\sqrt{2}-4\cdot3\sqrt{3}-2\cdot5\sqrt{3}+6\sqrt{3}\)
\(=10\sqrt{2}-12\sqrt{3}-10\sqrt{3}+6\sqrt{3}\)
\(=10\sqrt{2}-16\sqrt{3}\)
b: \(\sqrt{\left(3-\sqrt{6}\right)^2}+\sqrt{\left(1-\sqrt{6}\right)^2}\)
\(=\left|3-\sqrt{6}\right|+\left|1-\sqrt{6}\right|\)
\(=3-\sqrt{6}+\sqrt{6}-1\)
=3-1=2
c: \(\dfrac{5\sqrt{3}-3\sqrt{5}}{\sqrt{5}-\sqrt{3}}+\dfrac{1}{4+\sqrt{15}}\)
\(=\dfrac{\sqrt{15}\left(\sqrt{5}-\sqrt{3}\right)}{\sqrt{5}-\sqrt{3}}+\dfrac{1\left(4-\sqrt{15}\right)}{16-15}\)
\(=\sqrt{15}+4-\sqrt{15}=4\)
d: \(\dfrac{2\sqrt{3-\sqrt{5}}\cdot\left(3+\sqrt{5}\right)}{\sqrt{10}-\sqrt{2}}-\dfrac{\sqrt{15}+\sqrt{5}}{\sqrt{12}+2}\)
\(=\dfrac{\sqrt{3-\sqrt{5}}\cdot\sqrt{2}\left(3+\sqrt{5}\right)}{\sqrt{5}-1}-\dfrac{\sqrt{5}\left(\sqrt{3}+1\right)}{2\left(\sqrt{3}+1\right)}\)
\(=\dfrac{\sqrt{6-2\sqrt{5}}\cdot\left(3+\sqrt{5}\right)}{\sqrt{5}-1}-\dfrac{\sqrt{5}}{2}\)
\(=\sqrt{\left(\sqrt{5}-1\right)^2}\cdot\dfrac{\left(3+\sqrt{5}\right)}{\sqrt{5}-1}-\dfrac{\sqrt{5}}{2}\)
\(=3+\sqrt{5}-\dfrac{\sqrt{5}}{2}=3+\dfrac{\sqrt{5}}{2}\)
Bài 2:
Vẽ đồ thị:
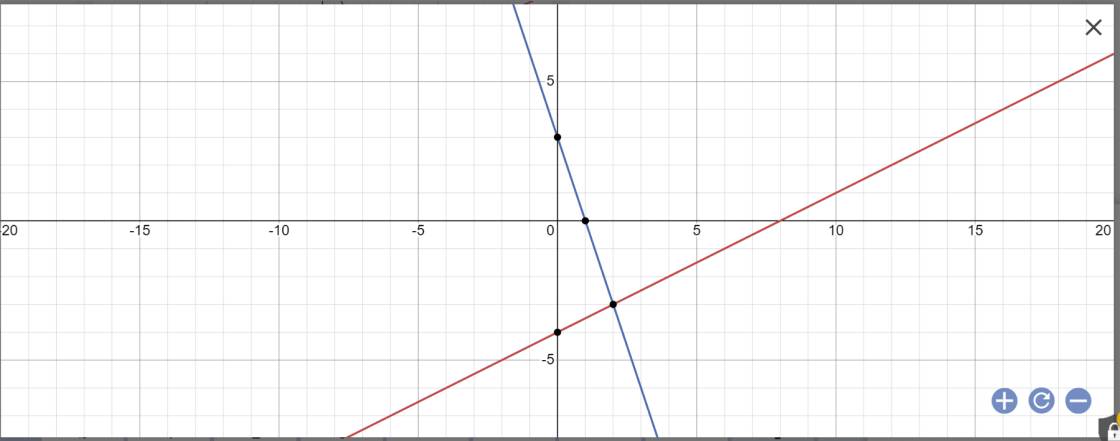
Phương trình hoành độ giao điểm là:
\(\dfrac{1}{2}x-4=-3x+3\)
=>\(\dfrac{1}{2}x+3x=3+4\)
=>\(\dfrac{7}{2}x=7\)
=>x=2
Thay x=2 vào y=-3x+3, ta được:
\(y=-3\cdot2+3=-3\)
Vậy: (d1) cắt (d2) tại A(2;-3)
Đúng 2
Bình luận (0)
Bài 2. Tính giá trị biểu thứca/ 2sqrt{27}-sqrt{frac{16}{3}}-sqrt{48}-sqrt{8frac{1}{3}}b/ left(3sqrt{20}-sqrt{125}-15sqrt{frac{1}{5}}right)sqrt{5}c/left(2sqrt{48}-frac{3}{2}sqrt{frac{4}{3}}+sqrt{27}right).2sqrt{3}d/ sqrt{left(3-2sqrt{2}right)^2}-sqrt{left(sqrt{8}-4right)^2}e/ sqrt{left(4-sqrt{15}right)^2}+sqrt{left(3-sqrt{15}right)^2}
Đọc tiếp
Bài 2. Tính giá trị biểu thức
a/ \(2\sqrt{27}-\sqrt{\frac{16}{3}}-\sqrt{48}-\sqrt{8\frac{1}{3}}\)
b/ \(\left(3\sqrt{20}-\sqrt{125}-15\sqrt{\frac{1}{5}}\right)\sqrt{5}\)
c/\(\left(2\sqrt{48}-\frac{3}{2}\sqrt{\frac{4}{3}}+\sqrt{27}\right).2\sqrt{3}\)
d/ \(\sqrt{\left(3-2\sqrt{2}\right)^2}-\sqrt{\left(\sqrt{8}-4\right)^2}\)
e/ \(\sqrt{\left(4-\sqrt{15}\right)^2}+\sqrt{\left(3-\sqrt{15}\right)^2}\)
Câu 1: Thực hiện phép tính
a,left(sqrt{12}+3sqrt{15}-4sqrt{135}right)cdotsqrt{3}
b,sqrt{252}-sqrt{700}+sqrt{1008}-sqrt{448}
c,2sqrt{40sqrt{12}}-2sqrt{sqrt{75}}-3sqrt{5sqrt{48}}
Câu 2: Rút gọn
a,frac{9sqrt{5}+3sqrt{27}}{sqrt{5}+sqrt{3}}
b,frac{3sqrt{8}+2sqrt{12}+sqrt{20}}{3sqrt{18}-2sqrt{27}+sqrt{45}}
c,left(4+sqrt{15}right)cdotleft(sqrt{10}-sqrt{6}right)cdotsqrt{4-sqrt{15}}
Câu 3:So sánh
a,3+sqrt{5}và2sqrt{2}+sqrt{6}
b,2sqrt{3}+4và3sqrt{2}+sqrt{10}
c,18vàsqrt{15}cdotsqrt{17}
Đọc tiếp
Câu 1: Thực hiện phép tính
\(a,\left(\sqrt{12}+3\sqrt{15}-4\sqrt{135}\right)\cdot\sqrt{3}\\ b,\sqrt{252}-\sqrt{700}+\sqrt{1008}-\sqrt{448}\\ c,2\sqrt{40\sqrt{12}}-2\sqrt{\sqrt{75}}-3\sqrt{5\sqrt{48}}\)
Câu 2: Rút gọn
\(a,\frac{9\sqrt{5}+3\sqrt{27}}{\sqrt{5}+\sqrt{3}}\\ b,\frac{3\sqrt{8}+2\sqrt{12}+\sqrt{20}}{3\sqrt{18}-2\sqrt{27}+\sqrt{45}}\\ c,\left(4+\sqrt{15}\right)\cdot\left(\sqrt{10}-\sqrt{6}\right)\cdot\sqrt{4-\sqrt{15}}\)
Câu 3:So sánh
\(a,3+\sqrt{5}và2\sqrt{2}+\sqrt{6}\\ b,2\sqrt{3}+4và3\sqrt{2}+\sqrt{10}\\ c,18và\sqrt{15}\cdot\sqrt{17}\)
Bài 1: Tính và rút gọn biểu thức:
Aleft(sqrt{5}+3right)left(5-sqrt{15}right)
Bleft(sqrt{32}-sqrt{50}+sqrt{27}right)left(sqrt{27}+sqrt{50}-sqrt{32}right)
C1-left(sqrt{45}-sqrt{20}-sqrt{3}right)left(sqrt{20}-sqrt{45}-sqrt{3}right)
Dleft(sqrt{frac{3}{2}}-sqrt{frac{2}{3}}right):frac{1}{sqrt{6}}
Đọc tiếp
Bài 1: Tính và rút gọn biểu thức:
\(A=\left(\sqrt{5}+3\right)\left(5-\sqrt{15}\right)\)
\(B=\left(\sqrt{32}-\sqrt{50}+\sqrt{27}\right)\left(\sqrt{27}+\sqrt{50}-\sqrt{32}\right)\)
\(C=1-\left(\sqrt{45}-\sqrt{20}-\sqrt{3}\right)\left(\sqrt{20}-\sqrt{45}-\sqrt{3}\right)\)
\(D=\left(\sqrt{\frac{3}{2}}-\sqrt{\frac{2}{3}}\right):\frac{1}{\sqrt{6}}\)
\(A=\left(\sqrt{5}+3\right)\left(5-\sqrt{15}\right)=5\sqrt{5}-5\sqrt{3}+15-3\sqrt{15}\)
Bạn ghi nhầm đề thì phải, ngoặc đầu là \(\sqrt{5}+\sqrt{3}\) mới rút gọn được theo HĐT số 3
\(B=\left(4\sqrt{2}-5\sqrt{2}+3\sqrt{3}\right)\left(3\sqrt{3}+5\sqrt{2}-4\sqrt{2}\right)\)
\(=\left(3\sqrt{3}-\sqrt{2}\right)\left(3\sqrt{3}+\sqrt{2}\right)=27-2=25\)
\(C=1-\left(3\sqrt{5}-2\sqrt{5}-\sqrt{3}\right)\left(2\sqrt{5}-3\sqrt{5}-\sqrt{3}\right)\)
\(=1-\left(\sqrt{5}-\sqrt{3}\right)\left(-\sqrt{5}-\sqrt{3}\right)=1+\left(5-3\right)=3\)
\(D=\left(\sqrt{\frac{3}{2}}-\sqrt{\frac{2}{3}}\right).\sqrt{6}=\frac{\left(3-2\right)}{\sqrt{6}}.\sqrt{6}=1\)
Đúng 0
Bình luận (0)