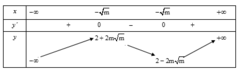
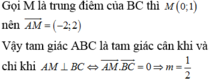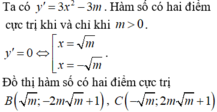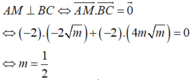Cho y = x3-3mx+1 có điểm A (2;3). Tìm m để hàm số có hai cực trị B,C sao cho tam giác ABC cân tại A

Những câu hỏi liên quan
Cho hàm số y=x3-3mx+1 (1). Cho A(2;3) tìm m để đồ thị hàm số (1) có hai điểm cực trị B và C sao cho tam giác ABC cân tại A
A. m=-1/2
B. m=-3/2
C. m=1/2
D. m=3/2
Cho hàm số
y
x
3
-
3
m
x
+
1
(1). Cho A(2;3) , tìm m để đồ thị hàm số (1) có hai điểm cực trị B và C sao cho tam giác ABC cân tại A.
Đọc tiếp
Cho hàm số y = x 3 - 3 m x + 1 (1). Cho A(2;3) , tìm m để đồ thị hàm số (1) có hai điểm cực trị B và C sao cho tam giác ABC cân tại A.
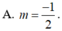
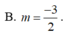
![]()
![]()
Khi đồ thị hàm số
y
x
3
-
3
m
x
+
2
có hai điểm cực trị A, B và đường tròn (C):
(
x
-
1
)
2
+
(
y
-
1
)
2
3
cắt đường thẳng AB tại hai điểm phân biệt M,N sao cho khoảng cách giữa M và N lớn nhất. Tính độ dài MN A. MN...
Đọc tiếp
Khi đồ thị hàm số y = x 3 - 3 m x + 2 có hai điểm cực trị A, B và đường tròn (C): ( x - 1 ) 2 + ( y - 1 ) 2 = 3 cắt đường thẳng AB tại hai điểm phân biệt M,N sao cho khoảng cách giữa M và N lớn nhất. Tính độ dài MN
A. MN= 3
B. MN=1.
C. MN=2.
D. MN=2 3
Cho hàm số
y
x
3
+
2
(
m
+
1
)
x
2
+
3
mx
+
2
có đồ thị (C) và điểm M(3;1). Tìm tham số m để đường thẳng d:y-x +2...
Đọc tiếp
Cho hàm số y = x 3 + 2 ( m + 1 ) x 2 + 3 mx + 2 có đồ thị (C) và điểm M(3;1). Tìm tham số m để đường thẳng d:y=-x +2 cắt đồ thị (C ) tại ba điểm phân biệt A(0;2),B,C sao cho tam giác MBC có diện tích bằng 2 6 .
A.m= -2.
B. m= -2 hoặc m= 3.
C. m= 3.
D. Không tồn tại m.
Cho đường thẳng
d
:
y
−
2
x
+
1
. Đồ thị của hàm số
y
x
3
−
3
mx
+
1
có hai điểm cực trị nằm trên đường thẳng d khi A. m 0 B. m 2 C. m
2
D. m 1
Đọc tiếp
Cho đường thẳng d : y = − 2 x + 1 . Đồ thị của hàm số y = x 3 − 3 mx + 1 có hai điểm cực trị nằm trên đường thẳng d khi
A. m = 0
B. m = 2
C. m = 2
D. m = 1
Cho hàm số y
x
3
+
2
m
+
1
x
2
+
3
m
x
+
2
có đồ thị (C) và điểm M(3;1). Tìm tham số m để đường thẳng d: y -x+2 cắt đồ thị (C) tại ba điểm phân biệt A(0;2),B,C sao cho tam giác MBC có diện tích bằng
2
6
A. m -2 B. m -2 hoặc m 3 C. m 3 D. K...
Đọc tiếp
Cho hàm số y = x 3 + 2 m + 1 x 2 + 3 m x + 2 có đồ thị (C) và điểm M(3;1). Tìm tham số m để đường thẳng d: y = -x+2 cắt đồ thị (C) tại ba điểm phân biệt A(0;2),B,C sao cho tam giác MBC có diện tích bằng 2 6
A. m = -2
B. m = -2 hoặc m = 3
C. m = 3
D. Không tồn tại m
Tìm tất cả các giá trị thực của tham số m để đồ thị của hàm số
y
-
x
3
+
3
m
x
+
1
có 2 điểm cực trị A,B sao cho tam giác OAB vuông tại O( với O là gốc tọa độ ). A.
m...
Đọc tiếp
Tìm tất cả các giá trị thực của tham số m để đồ thị của hàm số y = - x 3 + 3 m x + 1 có 2 điểm cực trị A,B sao cho tam giác OAB vuông tại O( với O là gốc tọa độ ).
A. m = 3 2
B. m = - 1 3
C. m = 1
D. m = 1 2
Chọn D
Ta có y ' = - 3 x 2 + 3 m
y ' = 0 ⇔ x 2 - m = 0 (*)
Đồ thị hàm số (1) có 2 điểm cực trị
⇔ P T ( * ) có 2 nghiệm phân biệt ⇔ m > 0 ( * * )
Khi đó 2 điểm cực trị
![]()
Tam giác OAB vuông tại O
![]()
V ậ y m = 1 2
Đúng 0
Bình luận (0)
Cho hàm số y = x 3 - 3 m x + 2 với m là tham số. Có bao nhiêu giá trị nguyên m < 2019 để hàm số có nhiều điểm cực trị nhất?
A. 2017
B. 2018
C. 4037
D. 4035
Tìm tất cả các giá trị thực của tham số m để hàm số y x3-3x2+3mx+1 có các điểm cực trị nhỏ hơn 2 A. -1 m B. m 1 C. m 0 D. 0 m 1
Đọc tiếp
Tìm tất cả các giá trị thực của tham số m để hàm số y= x3-3x2+3mx+1 có các điểm cực trị nhỏ hơn 2
A. -1> m
B. m< 1
C. m> 0
D. 0< m< 1
Ta có y’= 3x2-6x+3m
Yêu cầu bài toán khi y’=0 có hai nghiệm phân biệt x1<x2<2
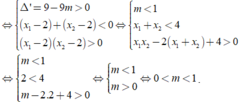
Chọn D.
Đúng 0
Bình luận (0)
Đồ thị hàm số
y
-
x
3
+
3
m
x
+
1
có 2 điểm cực trị A,B
x
A
x
B
sao cho tứ giác ABOE là hình bình hạnh với O là gốc tọa độ và điểm E(-4;-32). Tìm tất cả các giá trị thực của tham số m. A. m 1 B. m 4 C. m 2 D.
m...
Đọc tiếp
Đồ thị hàm số y = - x 3 + 3 m x + 1 có 2 điểm cực trị A,B x A < x B sao cho tứ giác ABOE là hình bình hạnh với O là gốc tọa độ và điểm E(-4;-32). Tìm tất cả các giá trị thực của tham số m.
A. m = 1
B. m = 4
C. m = 2
D. m ∈ ∅
Đáp án B.
Ta có y ' = - 3 x 2 + 3 m ; y ' = 0 ⇔ [ x = m ⇒ y = 2 m m + 1 ⇒ B ( m ; 2 m m + 1 ) x = - m ⇒ y = - 2 m m + 1 ⇒ A ( - m ; - 2 m m + 1 )
Do ABOE là hình bình hành nên A B = E O ⇒ 2 m = 4 4 m m = 32 ⇒ m = 4 .
Đúng 0
Bình luận (0)