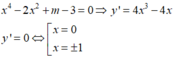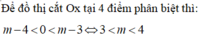Tìm m để y = -x4-mx2+m-1 cắt Ox tại 4 điểm

Những câu hỏi liên quan
Tìm tất cả các giá trị thực của tham số m để đồ thị hàm số
C
m
:
y
x
4
−
m
x
2
+
m
−
1
cắt trục hoành tại bốn điểm phân biệt. A.
m
1
m...
Đọc tiếp
Tìm tất cả các giá trị thực của tham số m để đồ thị hàm số C m : y = x 4 − m x 2 + m − 1 cắt trục hoành tại bốn điểm phân biệt.
A. m > 1 m ≠ 2
B. không có m
C. m > 1
D. m ≠ 2
Đáp án A
y ' = 4 x 3 − 2 mx
Để đồ thị cắt trục hoành tại 4 điểm phân biệt thì đồ thị hàm số phải có 3 cực trị và y C T < 0 < yCĐ Nên m>0 và y’=0 có 3 nghiệm
y ' = 0 ⇔ x= 0 x= 2 m 2 x=- 2 m 2
y C T < 0 < yCĐ ⇔ − m 2 4 + m − 1 < 0 < m − 1 ⇔ 2 ≠ m > 1
Đúng 0
Bình luận (0)
Tìm tất cả các giá trị thực của tham số m để đồ thị hàm số
C
m
:
y
x
4
−
m
x
2
+
m
−
1
cắt trục hoành tại bốn điểm phân biệt. A.
m
1
m...
Đọc tiếp
Tìm tất cả các giá trị thực của tham số m để đồ thị hàm số C m : y = x 4 − m x 2 + m − 1 cắt trục hoành tại bốn điểm phân biệt.
A. m > 1 m ≠ 2
B. không có m
C. m > 1
D. m ≠ 2
Đáp án A
y ' = 4 x 3 − 2 mx
Để đồ thị cắt trục hoành tại 4 điểm phân biệt thì đồ thị hàm số phải có 3 cực trị và y C T < 0 < yCĐ Nên m > 0 và y’=0 có 3 nghiệm
y ' = 0 ⇔ x= 0 x= 2 m 2 x=- 2 m 2
y C T < 0 < y C Đ ⇔ − m 2 4 + m − 1 < 0 < m − 1 ⇔ 2 ≠ m > 1
Đúng 0
Bình luận (0)
Cho hàm số
y
x
4
−
2
x
2
+
2
m
+
1
C
m
.
Tìm m để
C
m
cắt trục Ox tại 4 điểm phân biệt có hoành độ lập thành cấp số cộng. A.
m
−
4
9
B....
Đọc tiếp
Cho hàm số y = x 4 − 2 x 2 + 2 m + 1 C m . Tìm m để C m cắt trục Ox tại 4 điểm phân biệt có hoành độ lập thành cấp số cộng.
A. m = − 4 9
B. m = 4 ; m = − 4 9
C. m = 4
D. m = ± 4
Đáp án B
y = 0 ⇔ x 2 = 1 x 2 = 2 m + 1 . có 4 nghiệm phân biệt khi
2 m + 1 > 0 ; 2 m + 1 ≠ 1 ⇔ m > − 1 ; m ≠ 0 .
Khi đó 4 nghiệm là − 2 m + 1 ; − 1 ; 1 ; 2 m + 1
4 nghiệm lập thành cấp số cộng có trường hợp sau sắp xếp theo thứ tự sau
TH1: − 1 ; − 2 m + 1 ; 2 m + 1 ; 1 ⇒ khoảng cách giữa chúng là bằng nhau ⇔ 1 − 2 m + 1 = 2 2 m + 1 ⇔ 3 2 m + 1 = 1 ⇔ m = − 4 9 .
TH2: − 2 m + 1 ; − 1 ; 1 ; 2 m + 1 ⇒ khoảng cách giữa chung là bằng nhau
⇔ 2 m + 1 − 1 = 2 ⇔ m = 4
Đúng 0
Bình luận (0)
Cho hàm số
y
x
4
−
2
x
2
+
m
−
3
C
.Tất cả các giá trị của m để (C) cắt trục Ox tại 4 điểm phân biệt. A.
−
4
m
−
3
B.
3
m
4
C.
−
4
≤
m...
Đọc tiếp
Cho hàm số y = x 4 − 2 x 2 + m − 3 C .Tất cả các giá trị của m để (C) cắt trục Ox tại 4 điểm phân biệt.
A. − 4 < m < − 3
B. 3 < m < 4
C. − 4 ≤ m < 3
D. 3 < m ≤ 4
Đáp án là B
Phương trình hoành độ giao điểm của (C) và trục: x 4 − 2 x 2 + m − 3 = 0
Đặt t = x 2 ≥ 0 ⇒ t 2 − 2 t + m − 3 = 0 *
(C) cắt Ox tại 4 điểm phân biệt khi phương trình (*) có hai nghiệm phân biệt dương.
Δ ' > 0 S > 0 P > 0 ⇔ − m + 4 > 0 m − 3 > 0 ⇔ 3 < m < 4.
Đúng 0
Bình luận (0)
Cho hàm số y mx 2 − (d)1) Tìm m để (d) cắt Ox tại điểm có hoành độ là 22) Tìm m để (d) cắt Ox tại điểm có hoành độ lớn hơn 13) Tìm m để (d) cắt đường thẳng y x - 2m tại điểm có hoành độ là 14) Tìm m để (d) cắt y x + m - 1 tại điểm thuộc trục tung5) Tìm m để (d) cắt Ox, Oy tạo thành tam giác có diện tích là 26) Tìm m để (d) cắt Ox, Oy tạo thành tam giác vuông cân7) Tìm m để (d) cắt Ox, Oy tạo thành tam giác vuông có cạnh huyền là căn 5
Đọc tiếp
Cho hàm số y mx 2 = − (d)
1) Tìm m để (d) cắt Ox tại điểm có hoành độ là 2
2) Tìm m để (d) cắt Ox tại điểm có hoành độ lớn hơn 1
3) Tìm m để (d) cắt đường thẳng y = x - 2m tại điểm có hoành độ là 1
4) Tìm m để (d) cắt y = x + m - 1 tại điểm thuộc trục tung
5) Tìm m để (d) cắt Ox, Oy tạo thành tam giác có diện tích là 2
6) Tìm m để (d) cắt Ox, Oy tạo thành tam giác vuông cân
7) Tìm m để (d) cắt Ox, Oy tạo thành tam giác vuông có cạnh huyền là căn 5
Cho hàm số
y
x
4
-
2
x
2
+
m
-
3
C
. Tất cả các giá trị của m để đồ thị (C) cắt trục Ox tại 4 điểm phân biệt là A. -4 m -3 B. 3 m 4 C.
-
4
≤
m
3
D.
3
m
≤
4
Đọc tiếp
Cho hàm số y = x 4 - 2 x 2 + m - 3 C . Tất cả các giá trị của m để đồ thị (C) cắt trục Ox tại 4 điểm phân biệt là
A. -4 < m < -3
B. 3 < m < 4
C. - 4 ≤ m < 3
D. 3 < m ≤ 4
Đáp án B
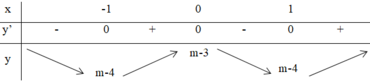
x 4 - 2 x 2 + m - 3 = 0 ⇒ y ' = 4 x 3 - 4 x y ' = 0 ⇔ [ x = 0 x = ± 1
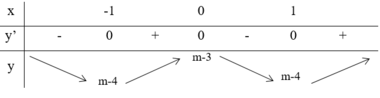
Để đồ thị cắt Ox tại 4 điểm phân biệt thì:
m - 4 < 0 < -3 <=> 3 < m < 4
Đúng 0
Bình luận (0)
Cho hàm số
y
x
4
−
2
x
2
+
m
−
3
C
.
Tất cả các giá trị của m để đồ thị (C) cắt trục Ox tại 4 điểm phân biệt là: A.
−
4
m
−
3.
B. ...
Đọc tiếp
Cho hàm số y = x 4 − 2 x 2 + m − 3 C . Tất cả các giá trị của m để đồ thị (C) cắt trục Ox tại 4 điểm phân biệt là:
A. − 4 < m < − 3.
B. 3 < m < 4.
C. − 4 ≤ m < 3.
D. 3 < m ≤ 4.
Tìm tất cả các giá trị thực của tham số m để hàm số
y
(
m
+
1
)
x
4
-
m
x
2
+
3
có ba điểm cực trị. A.
m
∈
(
-
∞
;
-
1
]
∪
[
0
;
+
∞...
Đọc tiếp
Tìm tất cả các giá trị thực của tham số m để hàm số y = ( m + 1 ) x 4 - m x 2 + 3 có ba điểm cực trị.
A. m ∈ ( - ∞ ; - 1 ] ∪ [ 0 ; + ∞ )
B. m ∈ ( - 1 ; 0 )
C. m ∈ ( - ∞ ; - 1 ] ∪ [ 0 ; + ∞ )
D. m ∈ ( - ∞ ; - 1 ) ∪ ( 0 ; + ∞ )
Cho hàm số
y
x
4
−
m
x
2
+
m
(m là tham số) có đồ thị
C
.
Biết rằng đồ thị (C) cắt trục hoành tại 4 điểm phân biệt có hoành độ
x
1
,
x
2
,
x
3
,
x
4
thỏa mãn...
Đọc tiếp
Cho hàm số y = x 4 − m x 2 + m (m là tham số) có đồ thị C . Biết rằng đồ thị (C) cắt trục hoành tại 4 điểm phân biệt có hoành độ x 1 , x 2 , x 3 , x 4 thỏa mãn x 1 4 + x 2 4 + x 3 4 + x 4 4 = 30 khi m = m 0 . Hỏi mệnh đề nào sau đây đúng?
A. 4 < m 0 ≤ 7
B. 0 < m 0 < 4
C. m 0 > 7
D. m 0 ≤ − 2
Đáp án A
Phương trình hoành độ giao điểm của (C) và Ox là x 4 − m x 2 + m = 0 * .
Đặt t = x 2 ≥ 0 khi đó * ⇔ f t = t 2 − m t + m = 0
Để (*) có 4 nghiệm phân biệt ⇔ f t = 0 có 2 nghiệm dương phân biệt t 1 , t 2
Khi đó, gọi t 1 , t 2 t 1 < t 2 là hai nghiệm phân biệt của f t = 0
Suy ra:
x 1 = − t 2 ; x 2 = − t 1 ; x 3 = t 1 ; x 4 = t 2 ⇒ x 1 4 + x 2 4 + x 3 4 + x 4 4 = 2 t 1 2 + t 2 2 = 30
Mà t 1 + t 2 = m t 1 t 2 = m
⇒ t 1 2 + t 2 2 = t 1 + t 2 2 − 2 t 1 t 2 = m 2 − 2 m
suy ra m > 4 m 2 − 2 m = 15 ⇔ m = 5.
Đúng 1
Bình luận (0)
Tìm
m
để đường thẳng
y
m
cắt đồ thị hàm số
y
x
4
−
2
x
2
+
2
tại 4 điểm phân biệt. A.
2
m
3
B.
m
2
C.
1
m
2
D. ...
Đọc tiếp
Tìm m để đường thẳng y = m cắt đồ thị hàm số y = x 4 − 2 x 2 + 2 tại 4 điểm phân biệt.
A. 2 < m < 3
B. m > 2
C. 1 < m < 2
D. m < 2
Đáp án là C.
• Xét hàm số y = x 4 − 2 x 2 + 2
+ y ' = 4 x 3 − 4 x , cho y ' = 0 ⇔ x = 0 ⇒ y = 2 x = ± 1 ⇒ y = 1
+ BBT
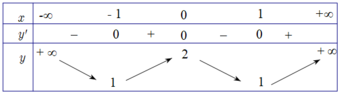
• Để đường thẳng y = m cắt đồ thị hàm số tại 4 điểm phân biệt thì 1 < m < 2.
Đúng 0
Bình luận (0)