Tìm m để y = x3+(m-3)x2+2mx+2 có cực đại, cực tiểu

Những câu hỏi liên quan
Tìm m để hàm số
y
-
x
3
+
(
2
m
-
1
)
x
2
+
(
m
-
2
)
x
-
2
có cực đại và cực tiểu A.
m
∈
-
∞
;
1
B.
m
∈
-
1
;...
Đọc tiếp
Tìm m để hàm số y = - x 3 + ( 2 m - 1 ) x 2 + ( m - 2 ) x - 2 có cực đại và cực tiểu
A. m ∈ - ∞ ; 1
B. m ∈ - 1 ; 5 4
C. m ∈ - ∞ ; 1 ∪ 5 4 ; + ∞
D. m ∈ - 1 ; + ∞
Ta có: y ' = - 3 x 2 + 2 ( 2 m - 1 ) x + m - 2 ( * )
Để hàm số đã cho có cực đại và cực tiểu khi và chỉ khi: phương trình có hai nghiệm phân biệt và y’ đổi dấu khi qua các nghiệm đó.
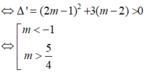
Chọn C.
Đúng 1
Bình luận (0)
Cho hàm số y f(x) -x3 + (2m – 1)x2 – (2 – m)x – 2. Tìm m để đồ thị hàm số có cực đại và cực tiểu? A. m ∈ (-1; +∞) B. m ∈ (-1; 5/4) C. m ∈ (-∞; -1) D. m ∈ (-∞; -1) ∪ (5/4; +∞)
Đọc tiếp
Cho hàm số y = f(x) = -x3 + (2m – 1)x2 – (2 – m)x – 2. Tìm m để đồ thị hàm số có cực đại và cực tiểu?
A. m ∈ (-1; +∞)
B. m ∈ (-1; 5/4)
C. m ∈ (-∞; -1)
D. m ∈ (-∞; -1) ∪ (5/4; +∞)
Đáp án D.
y = -x3 + (2m – 1)x2 – (2 – m)x – 2
TXĐ: D = R
y' = -3x2 + 2(2m – 1) – 2 + m
Đồ thị hàm số có cực đại và cực tiểu <=> Pt y’ = 0 có hai nghiệm phân biệt
<=> Δ’ = (2m – 1)2 + 3(-2 + m) > 0 <=> 4m2 – m – 5 > 0 <=> m ∈ (-∞; -1) ∪ (5/4; +∞)
Đúng 0
Bình luận (0)
Tìm giá trị của tham số m để hàm số
a) y = x 3 + (m + 3) x 2 + mx – 2 đạt cực tiểu tại x = 1
b) y = −( m 2 + 6m) x 3 /3 − 2m x 2 + 3x + 1 đạt cực đại tại x = -1;
a) y′ = 3 x 2 + 2(m + 3)x + m
y′ = 0 ⇔ 3 x 2 + 2(m + 3)x + m = 0
Hàm số đạt cực trị tại x = 1 thì:
y′(1) = 3 + 2(m + 3) + m = 3m + 9 = 0 ⇔ m = −3
Khi đó,
y′ = 3 x 2 – 3;
y′′ = 6x;
y′′(1) = 6 > 0;
Suy ra hàm số đạt cực tiểu tại x = 1 khi m = 3.
b) y′ = −( m 2 + 6m) x 2 − 4mx + 3
y′(−1) = − m 2 − 6m + 4m + 3 = (− m 2 − 2m – 1) + 4 = −(m + 1)2 + 4
Hàm số đạt cực trị tại x = -1 thì :
y′(−1) = − ( m + 1 ) 2 + 4 = 0 ⇔ ( m + 1 ) 2 = 4
⇔ 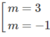
Với m = -3 ta có y’ = 9 x 2 + 12x + 3
⇒ y′′ = 18x + 12
⇒ y′′(−1) = −18 + 12 = −6 < 0
Suy ra hàm số đạt cực đại tại x = -1.
Với m = 1 ta có:
y′ = −7 x 2 − 4x + 3
⇒ y′′ = −14x − 4
⇒ y′′(−1) = 10 > 0
Suy ra hàm số đạt cực tiểu tại x = -1
Kết luận: Hàm số đã cho đạt cực đại tại x = -1 khi m = -3.
Đúng 0
Bình luận (0)
Tìm giá trị của m để đồ thị hàm số
y
x
3
-
3
x
2
+
2
có điểm cực đại và cực tiểu nằm về hai phía đối với đường tròn
C
m
:
x
2
+
y
2
-
2
m
x
-
4
m
y
+
5...
Đọc tiếp
Tìm giá trị của m để đồ thị hàm số y = x 3 - 3 x 2 + 2 có điểm cực đại và cực tiểu nằm về hai phía đối với đường tròn
C m : x 2 + y 2 - 2 m x - 4 m y + 5 m 2 - 1 = 0
A. 1 < m < 5 3
B. - 1 < m < 5 3
C. 3 5 < m < 1
D. - 3 5 < m < 1
· Đường tròn
C m : x 2 + y 2 - 2 m x - 4 m y + 5 m 2 - 1 = 0
có tâm I ( m;2m ), bán kính R = 1.Ta có:
I B = 5 m 2 + 4 m + 8 = 5 m + 2 5 2 + 36 5 ≥ 6 5 > 1 = R
điểm B nằm ở phía ngoài đường tròn C m . Do đó điểm A nằm ở phía trong đường tròn C m , tức là:
L A < 1 = R ⇔ 5 m 2 - 8 m + 4 < 1 ⇔ 5 m 2 - 8 m + 3 < 0 ⇔ 3 5 < m < 1
Đáp án C
Đúng 0
Bình luận (0)
1.y=\(\dfrac{1}{3}x^3-2mx^2+3x+1\) tìm m để hs có cực đại, cực tiểu
2. y=\(x^3-mx^2+\left(m^2-6\right)x+1\) tìm m để hs đạt cực trị tại x=1, khi đó hs là điểm cực đại hay cực tiểu
Xác định m để hàm số: y = x 3 − m x 2 + (m – 2/3)x + 5 có cực trị tại x = 1. Khi đó, hàm số đạt cực tiểu hay đạt cực đại? Tính cực trị tương ứng.
Ta biết hàm số y = f(x) có cực trị khi phương trình y’ = 0 có nghiệm và y’ đổi dấu khi qua các nghiệm đó.
Ta có:
Xét y’ = 0, ta có: y′ = 3 x 2 − 2mx + (m – 2/3)
∆ ’ > 0 khi m < 1 hoặc m > 2 (∗)
Để hàm số có cực trị tại x = 1 thì
y′(1) = 3 − 2m + m – 2/3 = 0 ⇔ m = 7/3, thỏa mãn điều kiện (∗)
Với m = 7/3 thì hàm số đã cho trở thành:
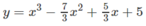
Ta có:
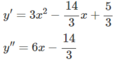
Vì y′′(1) = 6 – (14/3) > 0 nên hàm số đạt cực tiểu tại x = 1 và y CT = y(1) = (16/3).
Đúng 0
Bình luận (0)
Xác định m để hàm số: y = x 3 − m x 2 + (m – 2/3)x + 5 có cực trị tại x = 1. Khi đó, hàm số đạt cực tiểu hay đạt cực đại? Tính cực trị tương ứng.
Ta biết hàm số y = f(x) có cực trị khi phương trình y’ = 0 có nghiệm và y’ đổi dấu khi qua các nghiệm đó.
Ta có:
Xét y’ = 0, ta có: y′ = 3 x 2 − 2mx + (m – 2/3)
Δ’ > 0 khi m < 1 hoặc m > 2 (∗)
Để hàm số có cực trị tại x = 1 thì
y′(1) = 3 − 2m + m – 2/3 = 0 ⇔ m = 7/3, thỏa mãn điều kiện (∗)
Với m = 7/3 thì hàm số đã cho trở thành:
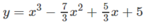
Ta có:
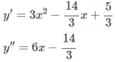
Vì y′′(1) = 6 – (14/3) > 0 nên hàm số đạt cực tiểu tại x = 1 và y C T = y(1) = (16/3).
Đúng 0
Bình luận (0)
Xác định giá trị của tham số m để hàm số y = x 3 + m x 2 - 3 có cực đại và cực tiểu.
A. m = 3; B. m > 0;
C. m ≠ 0; D. m < 0.
Đáp án: C.
Để có cực đại, cực tiểu, phương trình y' = 3 x 2 + 2mx = 0 phải có hai nghiệm phân biệt.
Phương trình y' = x(3x + 2m) = 0 có hai nghiệm phân biệt x1 = 0, x2 = -2m/3 khi và chỉ khi x ≠ 0.
Đúng 0
Bình luận (0)
Xác định giá trị của tham số m để hàm số y = x 3 + m x 2 - 3 có cực đại và cực tiểu.
A. m = 3; B. m > 0;
C. m ≠ 0; D. m < 0.
Đáp án: C.
Để có cực đại, cực tiểu, phương trình y' = 3 x 2 + 2mx = 0 phải có hai nghiệm phân biệt.
Phương trình y' = x(3x + 2m) = 0 có hai nghiệm phân biệt x 1 = 0, x 2 = -2m/3 khi và chỉ khi x ≠ 0.
Đúng 0
Bình luận (0)




