Dao động điều hòa có phương trình x=Acos(omega t+fi). Lúc t=0 vật cách vị trí cân bằng 2 (cm) và có
gia tốc -100 căn 2 (cm/ s2), vận tốc 10 căn 2 ( cm s ). Viết phương trình dao động:

Những câu hỏi liên quan
Một vật dao động điều hòa với tần số góc
ω
5 rad/s. Lúc t 0, vật đi qua vị trí có li độ là x -2 cm và có vận tốc 10 cm/s hướng về phía vị trí biên gần nhất. Phương trình dao động của vật là A.
x
2
cos
(
5
t
+
5
π
4
)
(cm) B.
x
...
Đọc tiếp
Một vật dao động điều hòa với tần số góc ω = 5 rad/s. Lúc t = 0, vật đi qua vị trí có li độ là x = -2 cm và có vận tốc 10 cm/s hướng về phía vị trí biên gần nhất. Phương trình dao động của vật là
A. x = 2 cos ( 5 t + 5 π 4 ) (cm)
B. x = 2 2 cos ( 5 t + 3 π 4 )
C. x = 2 cos ( 5 t - π 4 )
D. x = 2 2 cos ( 5 t + π 4 )
Đáp án B
Vật đi qua vị trí có li độ là x = -2 cm và đang hướng về phía vị trí biên gần nhất nên: v = -10 cm/s
Biên độ dao động của vật: A 2 = x 2 + v 2 ω 2 = ( - 2 ) 2 + ( - 10 ) 2 5 2 ⇒ A = 2 2 cm
Tại thời điểm ban đầu:
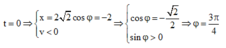
Phương trình dao động của vật là: x = 2 2 cos ( 5 t + 3 π 4 )
Đúng 0
Bình luận (0)
Một vật dao động điều hòa với tần số góc
ω
5
rad/s. Lúc t 0, vật đi qua vị trí có li độ là
x
−
2
cm
và có vận tốc 10 cm/s hướng về phía vị trí biên gần nhất. Phương trình dao động của vật là A.
x
2
cos
5
t
+
5...
Đọc tiếp
Một vật dao động điều hòa với tần số góc ω = 5 rad/s. Lúc t = 0, vật đi qua vị trí có li độ là x = − 2 cm và có vận tốc 10 cm/s hướng về phía vị trí biên gần nhất. Phương trình dao động của vật là
A. x = 2 cos 5 t + 5 π 4 cm
B. x = 2 2 cos 5 t + 3 π 4 cm
C. x = 2 cos 5 t − π 4 cm
D. x = 2 2 cos 5 t + π 4 cm
Đáp án B
Vật đi qua vị trí có li độ là x = − 2 cm và đang hướng về phía vị trí biên gần nhất nên: v = − 10 cm / s
Biên độ dao động của vật:
A 2 = x 2 + v 2 ω 2 = − 2 2 + − 10 2 5 2 = 8 ⇒ A = 2 2 cm
Tại thời điểm ban đầu:
t = 0 ⇒ x = 2 2 cosφ = − 2 v < 0 ⇒ cosφ = − 2 2 sinφ > 0 ⇒ φ = 3 π 4
Phương trình dao động của vật là: x = 2 2 cos 5 t + 3 π 4 cm
Đúng 0
Bình luận (0)
Một vật có khối lượng m 1 kg dao động điều hòa theo phương ngang với chu kì T 2 s. Biết khi vật đi qua vị trí cân bằng thì vận tốc là 10π cm/s. Chọn t 0 là lúc vật đi qua vị trí cân bằng theo chiều dương. Phương trình dao động điều hòa của vật là A. x 10cos(πt – 0,5π) cm. B. x 7cos(3πt) cm. C. x 8cos(2πt + 0,25π) cm D. x 6cos(5πt + π/3) cm.
Đọc tiếp
Một vật có khối lượng m = 1 kg dao động điều hòa theo phương ngang với chu kì T = 2 s. Biết khi vật đi qua vị trí cân bằng thì vận tốc là 10π cm/s. Chọn t = 0 là lúc vật đi qua vị trí cân bằng theo chiều dương. Phương trình dao động điều hòa của vật là
A. x = 10cos(πt – 0,5π) cm.
B. x = 7cos(3πt) cm.
C. x = 8cos(2πt + 0,25π) cm
D. x = 6cos(5πt + π/3) cm.
Một vật có khối lượng m 1 kg dao động điều hòa theo phương ngang với chu kì T 2 s. Biết khi vật đi qua vị trí cân bằng thì vận tốc là 10π cm/s. Chọn t 0 là lúc vật đi qua vị trí cân bằng theo chiều dương. Phương trình dao động điều hòa của vật là A. x 10cos(πt – 0,5π) cm B. x 7cos(3πt) cm C. x 8cos(2πt + 0,25π) cm D. x 6cos(5πt + π/3) cm
Đọc tiếp
Một vật có khối lượng m = 1 kg dao động điều hòa theo phương ngang với chu kì T = 2 s. Biết khi vật đi qua vị trí cân bằng thì vận tốc là 10π cm/s. Chọn t = 0 là lúc vật đi qua vị trí cân bằng theo chiều dương. Phương trình dao động điều hòa của vật là
A. x = 10cos(πt – 0,5π) cm
B. x = 7cos(3πt) cm
C. x = 8cos(2πt + 0,25π) cm
D. x = 6cos(5πt + π/3) cm
Đáp án A
Tần số gốc của dao động
![]()
Tốc độ của vật qua vị trí cân bằng là tốc độ cực đại
![]()
→ x = 10cos(πt – 0,5π) cm
Đúng 0
Bình luận (0)
Một vật dao động điều hòa theo phương ngang, khi lệch ra khỏi vị trí cân bằng 10(cm) thì vật có vận tốc bằng không. Biết vật dao động với chu kì 2(s) và chọn gốc thời gian lúc chất điểm đi qua vị trí có li độ cực đại?
a/ Viết phương trình dao động của vật ?
b/ Viết biểu thức vận tốc, gia tốc tức thời ? Tính vận tốc cực đại ? Tính gia tốc cực đại ?
c/ Ở thời điểm t 0,25(s) hãy tính pha dao động ? Tính li độ ? Tính vận tốc ? Tính gia tốc và cho biết ở thời điểm đó chất điểm chuyển động nhanh dần...
Đọc tiếp
Một vật dao động điều hòa theo phương ngang, khi lệch ra khỏi vị trí cân bằng 10(cm) thì vật có vận tốc bằng không. Biết vật dao động với chu kì 2(s) và chọn gốc thời gian lúc chất điểm đi qua vị trí có li độ cực đại? a/ Viết phương trình dao động của vật ? b/ Viết biểu thức vận tốc, gia tốc tức thời ? Tính vận tốc cực đại ? Tính gia tốc cực đại ? c/ Ở thời điểm t = 0,25(s) hãy tính pha dao động ? Tính li độ ? Tính vận tốc ? Tính gia tốc và cho biết ở thời điểm đó chất điểm chuyển động nhanh dần hay chậm dần ?
Một vật dao động điều hòa có phương trình vận tốc (t tính bằng (a) thì quỹ đạo dao động dài 20 cm.(b) tốc độ cực đại của vật là 5 cm/s.(c) gia tốc của vật có độ lớn cực đại là
20
2
c
m
/
s
2
.
(d) tần số của dao động là 2 Hz.(e) tốc độ trung bình của vật trong một chu kì dao động là 20 cm/s.(f) tại thời điểm ban đầu (
t
...
Đọc tiếp
Một vật dao động điều hòa có phương trình vận tốc (t tính bằng
(a) thì quỹ đạo dao động dài 20 cm.
(b) tốc độ cực đại của vật là 5 cm/s.
(c) gia tốc của vật có độ lớn cực đại là 20 2 c m / s 2 .
(d) tần số của dao động là 2 Hz.
(e) tốc độ trung bình của vật trong một chu kì dao động là 20 cm/s.
(f) tại thời điểm ban đầu ( t = 0 ), vật đi qua vị trí cân bằng.
Trong các phát biểu trên, phát biểu đúng là?
A. (b) và (e).
B. (a) và (d).
C. (c) và (e).
D. (a) và (c).
+ Từ phương trình v = 10 π c os 2 π t + 0 , 5 π = ω A cos 2 π t + φ + π 2
® x = 5 cos 2 π t .
® Quỹ đạo dao động là: L = 2 A = 10 cm
Tốc độ cực đại là v max = 10 π cm/s
Gia tốc cực đại là a max = ω 2 A = 20 π 2 c m / s 2
Tốc độ trung bình trong một chu kì là v t b = s T = 4 A T = 4.5 1 = 20 cm/s.
Tại t = 0 thì x = 5 ® vật ở vị trí biên.
® Các phát biểu đúng là: c, e.
Đáp án C
Đúng 0
Bình luận (0)
Một con lắc lò xo dao động điều hòa với phương trình x Acos(ωt + φ) cm. Tại thời điểm t1, vật có vận tốc v1 50 cm/s, gia tốc a1 -10√3 m/s2. Tại thời điểm t2 t1 + Δt (Δt 0), vật có vận tốc là v2 -50√2 cm/s, gia tốc a2 10√2 m/s2. Gía trị nhỏ nhất của Δt:
Đọc tiếp
Một con lắc lò xo dao động điều hòa với phương trình x = Acos(ωt + φ) cm. Tại thời điểm t1, vật có vận tốc v1 = 50 cm/s, gia tốc a1 = -10√3 m/s2. Tại thời điểm t2 = t1 + Δt (Δt > 0), vật có vận tốc là v2 = -50√2 cm/s, gia tốc a2 = 10√2 m/s2. Gía trị nhỏ nhất của Δt:
![]()
![]()
Chọn A
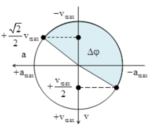
+ Với hai đại lượng vuông pha a và v, ta có phương trình độc lập:

+ Với hai thời điểm t1 và t2 ta có hệ:
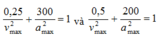
=> ω = 20 rad/s và vmax = 100 cm/s.
+ Từ hình vẽ xác định được khoảng thời gian tương ứng là:
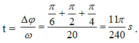
Đúng 0
Bình luận (0)
Một vật dao động điều hòa x=Acos( ωt+ φ). Trong khoảng 1/60s đầu tiên vật đi từ vị trí Xo=0 đến vị trí X=A √3/2 theo chiều dương và tại điểm cách vị trí cân bằng 2cm vật có vận tốc 40π√3 cm/s. Viết phương trình li độ
+ Biểu diễn dao động điều hoà bằng véc tơ quay.
Trong 1/60s đầu tiên ứng với véc tơ quay từ M đến N, góc quay dễ dàng tìm được là 600.
Thời gian \(t=\dfrac{60}{360}T=\dfrac{1}{60}\Rightarrow T = 0,1s\)
\(\Rightarrow \omega = 2\pi/T=20\pi (rad/s)\)
Áp dụng công thức độc lập: \(A^2=x^2+\dfrac{v^2}{\omega^2}\Rightarrow A^2=2^2+\dfrac{(40\pi\sqrt 3)^2}{20\pi}\)
\(\Rightarrow A = 4cm\)
Pha ban đầu ứng với véc tơ quay tại M \(\Rightarrow \varphi = -\dfrac{\pi}{2} (rad/s)\)
Vậy: \(x=4\cos(20\pi t -\dfrac{\pi}{2}) (cm)\)
Đúng 0
Bình luận (0)

Vật đi từ li độ x =0 theo chiều dương đến li độ x = \(A\sqrt{3}/2\) như hình vẽ.
Cung quay được tương ứng có màu đỏ và bằng \(\phi = 90- \varphi = 60^0.\) (vì \(\cos\varphi = \frac{A\sqrt{3}/2}{A}= \frac{\sqrt{3}}{2} \Rightarrow \varphi = 30^0. \))
Thời gian quay là \(t = \frac{\pi/3}{\omega} = \frac{1}{60} \Rightarrow \omega = \pi/3:\frac{1}{60}=20\pi. \)(rad/s).
ADCT mối quan hệ giữa li độ, vận tốc tại li độ đó và biên độ
\(A^2 = x^2 + \frac{v^2}{\omega}=2^2+\frac{40^2\pi^2\sqrt{3}^2}{20^2\pi^2} = 16.\)
=> A = 4cm.
Do vật đi từ x = 0 theo chiều dương nên hình vào hình tròn va thấy \(\varphi = -\frac{\pi}{2}.\)
=> \(x = 4 \cos (20\pi t - \frac{\pi}{2}).\)
Đúng 1
Bình luận (0)
. Một vật dao động điều hoà dọc theo trục Ox. Lúc vật qua vị trí có li độ x = -√2 cm thì có vận tốc v = -π√2 cm/s và gia tốc a = π2√2 cm/s2. Chọn gốc toạ độ ở vị trí trên. Phương trình dao động của vật dưới dạng hàm số sin.









