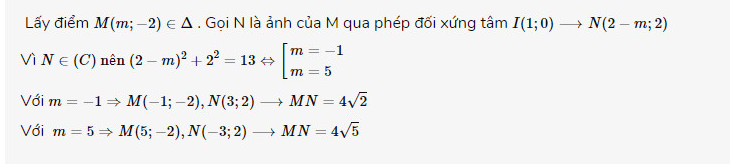Cho (C) : x2+y2-2x-2my+m2-24=0 có tâm I và đường thẳng Δ: mx + 4y = 0. Tìm m biết đường thẳng Δ cắt (C) tại 2 điểm phân biệt A,B thoả mãn SIAB = 12.

Những câu hỏi liên quan
Trong không gian tọa độ Oxyz cho mặt cầu (S): x2 + y2 + z2 + 4x - 6y + m 0 và đường thẳng Δ là giao tuyến của hai mặt phẳng (α): x + 2y - 2z - 4 0 và (β): 2x - 2y - z + 1 0. Đường thẳng Δ cắt mặt cầu (S) tại hai điểm phân biệt A, B thỏa mãn AB 8 khi: A. m 12 B. m -12 C. m -10 D. m 5
Đọc tiếp
Trong không gian tọa độ Oxyz cho mặt cầu (S): x2 + y2 + z2 + 4x - 6y + m = 0 và đường thẳng Δ là giao tuyến của hai mặt phẳng (α): x + 2y - 2z - 4 = 0 và (β): 2x - 2y - z + 1 = 0. Đường thẳng Δ cắt mặt cầu (S) tại hai điểm phân biệt A, B thỏa mãn AB = 8 khi:
A. m = 12
B. m = -12
C. m = -10
D. m = 5
Chọn B
Phương trình (S): x2 + y2 + z2 + 4x - 6y + m = 0 là phương trình mặt cầu <=> m < 13
Khi đó (S) có tọa độ tâm I (-2;3;0) bán kính ![]()
Gọi M (x;y;z) là điểm bất kỳ thuộc Δ.
Tọa độ M thỏa mãn hệ: 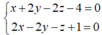
Đặt y = t ta có: 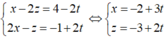
=> Δ có phương trình tham số: 
Δ đi qua điểm N (-2; 0; -3) và có vectơ chỉ phương ![]()
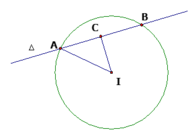
Giả sử mặt cầu (S) cắt Δ tại hai điểm phân biệt A, B sao cho AB = 8. Gọi (C) là đường tròn lớn chứa đường thẳng Δ. Khi đó IC2 = R2 - AC2 = 13 - m - 42 = -m - 3
N (0;-3;-3)

Vậy mặt cầu (S) cắt Δ tại hai điểm phân biệt A, B sao cho AB = 8
<=> -m - 3 = 9 <=> m = -12
Đúng 0
Bình luận (0)
trong mặt phẳng Oxy, cho điểm I (2;-1) và đường thẳng Δ:3x+4y+3=0.Viết phương trình đường tròn tâm I cắt Δ tại hai điểm phân biệt A,B sao cho diện tích tam giác IAB = 4
gọi H là trung điểm AB
=> \(IH=d_{\left(I,\Delta\right)}=\dfrac{\left|3\cdot2+4\cdot\left(-1\right)+3\right|}{\sqrt{3^2+4^2}}=1\)
\(S_{\Delta IAB}=2\cdot\left(\dfrac{1}{2}\cdot IH\cdot HA\right)=4\)
\(IH\cdot IA=4\Leftrightarrow1\cdot HA=4\Rightarrow HA=4\)
\(\Rightarrow R=IA=\sqrt{IH^2+HA^2}=\sqrt{1^2+4^2}=\sqrt{17}\)
\(\Rightarrow\) Phương trình đường tròn (x-2)2 +(y+1)2=17
Đúng 1
Bình luận (0)
Trong không gian với hệ trục tọa độ Oxyz, cho đường thẳng
△
:
x
1
+
t
y
1
+
m
t
z...
Đọc tiếp
Trong không gian với hệ trục tọa độ Oxyz, cho đường thẳng △ : x = 1 + t y = 1 + m t z = - 2 t và mặt cầu
(S): x 2 + y 2 + z 2 - 2x + 4y - 2z + 2 = 0 Với điều kiện nào của m thì đường thẳng Δ cắt (S) tại hai điểm phân biệt?
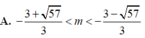
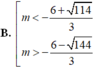
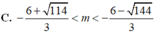
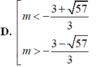
Chọn B
Mặt cầu (S) có tâm I(1;−2;1), bán kính R=2.
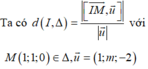
là véctơ chỉ phương của đường thẳng Δ.
Để đường thẳng cắt mặt cầu (S) tại hai điểm phân biệt thì khoảng cách từ tâm I đến đường thẳng Δ phải nhỏ hơn bán kính R.
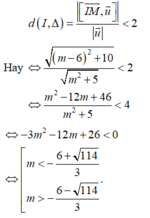
Đúng 0
Bình luận (0)
Trong không gian với hệ trục tọa độ Oxyz, cho đường thẳng
∆
:
x
1
+
t
y
1
+
m
t
z...
Đọc tiếp
Trong không gian với hệ trục tọa độ Oxyz, cho đường thẳng ∆ : x = 1 + t y = 1 + m t z = - 2 t và mặt cầu S : x 2 + y 2 + z 2 - 2 x + 4 y - 2 z + 2 = 0 . Với điều kiện nào của m thì đường thẳng Δ cắt (S) tại hai điểm phân biệt?
A. - 3 + 57 3 < m < - 3 - 57 3
B. m < - 6 + 114 3 hoặc m > - 6 - 114 3
C. - 6 + 114 3 m < - 6 - 114 3 hoặc m > - 6 - 114 3
D. m < - 3 + 57 3 hoặc m > - 3 - 57 3
Đáp án B
Mặt cầu (S) có tâm I(1;−2;1), bán kính R=2.

Để đường thẳng cắt mặt cầu (S) tại hai điểm phân biệt thì khoảng cách từ tâm I đến đường thẳng Δ phải nhỏ hơn bán kính R.
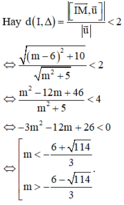
Đúng 0
Bình luận (0)
Cho đường tròn (C): (x - 1
)
2
+ (y + 3
)
2
10 và đường thẳng Δ: x + y + 1 0, biết đường tròn (C) cắt Δ tại hai điểm phân biệt A và B. Độ dài đoạn thẳng AB bằng: A.
19
2
B.
38
C.
19
2
D.
38
2
Đọc tiếp
Cho đường tròn (C): (x - 1 ) 2 + (y + 3 ) 2 = 10 và đường thẳng Δ: x + y + 1 = 0, biết đường tròn (C) cắt Δ tại hai điểm phân biệt A và B. Độ dài đoạn thẳng AB bằng:
A. 19 2
B. 38
C. 19 2
D. 38 2
Chọn B.
Vì đường tròn (C) cắt Δ tại hai điểm phân biệt A và B nên tọa độ điểm A và B là nghiệm của hệ phương trình:
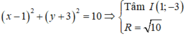
Gọi H là trung điểm của AB suy ra IH ⊥ AB ⇒ IH ⊥ Δ.
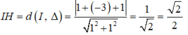
Xét tam giác AIH vuông tại H ta có:
A H 2 + I H 2 = A I 2 ⇒ A H 2 = A I 2 - I H 2
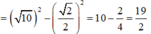
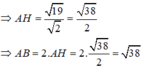
Đúng 1
Bình luận (0)
Cho (C):x2+y2-2x-2my+m2-24=0. Có tâm I và đường thẳng d: mx+4y=0. Tìm m để d giao (C) tại 2 điểm phân biệt A,B mà SABC=12
Viết lại pt (C):
\(\left(x-1\right)^2+\left(y-m\right)^2=25\) \(\Rightarrow\left\{{}\begin{matrix}I\left(1;m\right)\\R=5\end{matrix}\right.\)
Ý bạn là tam giác ABI? Không thấy C nào ở đây
Đặt \(d\left(I;AB\right)=k\)
Ta có \(S_{ABI}=\frac{1}{2}AB.d\left(I;AB\right)=\frac{AB}{2}.k=\sqrt{R^2-k^2}.k=12\)
\(\Rightarrow k^2\left(R^2-k^2\right)=144\Rightarrow k^4-25k^2+144=0\Rightarrow\left[{}\begin{matrix}k^2=16\\k^2=9\end{matrix}\right.\)
Áp dụng công thức khoảng cách:
\(d\left(I;AB\right)=\frac{\left|m+4m\right|}{\sqrt{m^2+16}}=k\Leftrightarrow\left|5m\right|=k\sqrt{m^2+16}\)
\(\Leftrightarrow25m^2=k^2m^2+16k^2\)
- Với \(k^2=16\Rightarrow25m^2=16m^2+16^2\Rightarrow m^2=\left(\frac{16}{9}\right)^2\Rightarrow m=\pm\frac{16}{9}\)
- Với \(k^2=9\Rightarrow25m^2=9m^2+144\Rightarrow16m^2=144\Rightarrow m=\pm3\)
Đúng 0
Bình luận (0)
Trong mặt phẳng Oxy cho đường thẳng Δ : y + 2 = 0 và đường tròn (C) : x2 + y2 = 13. qua phép đối xứng tâm I ( 0;1) điểm M trên đường thẳng Δ biến thành điểm M thuộc (C). Độ dài nhỏ nhát của đoạn MN bằng bào nhiêu?
M thuộc Δ nên M (t ; - 2) với t là số thực
Sau khi thực hiện phép đối xứng qua tâm I (0 ; 1) thì M biến thành N (- t ; 4)
N nằm trên (C) nên t2 + 16 = 13. Vô lí, xem lại đề bài xem có sai không bạn ơi
Đúng 0
Bình luận (0)
Cho đường tròn ( C) : x^2 + y^2 - 2x + 4y - 4 = 0, có tâm I và đường thẳng d : √2x + my + 1 - √2 = 0
a) Tìm m để đường thẳng cắt đường tròn (C) tại hai điểm phân biệt A, B
b) Tìm m để diện tích tam giác IAB là lớn nhất
Đường tròn (C) tâm \(I\left(1;-2\right)\) bán kính \(R=3\)
a. Đường thẳng cắt đường tròn tại 2 điểm pb khi:
\(d\left(I;d\right)< R\Leftrightarrow\dfrac{\left|\sqrt{2}-2m+1-\sqrt{2}\right|}{\sqrt{2+m^2}}< 3\)
\(\Leftrightarrow\left(2m-1\right)^2< 9\left(m^2+2\right)\)
\(\Leftrightarrow8m^2+4m+17>0\) (luôn đúng)
Vậy đường thẳng luôn cắt đường tròn tại 2 điểm pb với mọi m
b. \(S_{IAB}=\dfrac{1}{2}IA.IB.sin\widehat{AIB}=\dfrac{1}{2}R^2.sin\widehat{AIB}\le\dfrac{1}{2}R^2\) do \(sin\widehat{AIB}\le1\)
Dấu "=" xảy ra khi \(sin\widehat{AIB}=1\Rightarrow\Delta IAB\) vuông cân tại I
\(\Rightarrow d\left(I;d\right)=\dfrac{R}{\sqrt{2}}\Leftrightarrow\dfrac{\left|2m-1\right|}{\sqrt{m^2+2}}=\dfrac{3}{\sqrt{2}}\)
\(\Leftrightarrow m^2+8m+16=0\Rightarrow m=-4\)
Đúng 0
Bình luận (1)
Cho Parabol(P) : y=x² và đường thăng (d) : y=(2m-1)x-m+2 ( m là tham số)
A) c)m rằng với mới m đường thẳng (d) luôn cắt (P) tại 2 điểm phân biệt
B)Tìm các giá trị m để đường thẳng (d) cắt Parabol (P) tại hai điểm phân biệt A(x1;y1);B(x2;y2) thoả mãn x1y1+x2y2=0
xét phương trình hoành độ giao điểm : \(x^2=\left(2m-1\right)x-m+2\)\(\Leftrightarrow x^2-\left(2m-1\right)x+m-2=0\)có \(\Delta=\left(2m-1\right)^2-4\left(m-2\right)=4m^2-8m+9=\left(2m-1\right)^2+8\ge8\)vậy nên phương trinh luôn có 2 nghiệm phân biệt tức hai đồ thị luôn cắt nhau tại 2 điểm phân biệt A và BCó viet : \(\hept{\begin{cases}x_1+x_2=2m-1\\x_1x_2=m-2\end{cases}}\)ta có : \(A\left(x_1,y_1\right)=A\left(x_1,x_1^2\right)\)và \(B\left(x_2,y_2\right)=B\left(x_2,x_2^2\right)\)
nên ta có : \(x_1y_1+x_2y_2=0\Leftrightarrow x_1^3+x_2^3=0\)\(\Leftrightarrow\left(x_1+x_2\right)\left(\left(x_1+x_2\right)^2-3x_1x_2\right)=0\)\(\Leftrightarrow\left(2m-1\right)\left[\left(2m-1\right)^2-3m+6\right]=0\)
\(2m-1=0\Leftrightarrow m=\frac{1}{2}\)\(\left(2m-1\right)^2-3m+6=0\Leftrightarrow4m^2-7m-7=0\)VN
Đúng 1
Bình luận (0)
2. Cho parabol (P): y = x2 và đường thẳng (d): y = 2(m – 1)x + m2 + 2m (m là tham số, m ∈ R )
a) Chứng minh rằng đường thẳng (d) luôn cắt parabol (P) tại hai điểm phân biệt A, B?
b) Gọi H và K lần lượt là hình chiếu của A và B trên trục hoành.
Tìm m sao cho: OH2 + OK2 = 6 mọi người hướng dẫ mk ý b vs
Đúng 0
Bình luận (0)